Instability inspection of parametric vibrating rectangular Mindlin plates lying on Winkler foundations under periodic loading of moving masses

E. Torkan·M. Pirmoradian·M. Hashemian

Received:10 May 2018/Revised:27 June 2018/Accepted:30 July 2018/Published online:29 October 2018

©The Chinese Society of Theoretical and Applied Mechanics；Institute of Mechanics,Chinese Academy of Sciences and Springer-Verlag GmbH Germany,part of Springer Nature 2018

Abstract Parametric resonance is one of the most important issues in the study of dynamical behavior of structures. In this paper,dynamic instability of a moderately thick rectangular plate on an elastic foundation is investigated in the case of parametric and external resonances due to periodic passage of moving masses. The governing coupled partial differential equations(PDEs) of the system, with consideration of the first-order shear deformation theory (FSDT) or Mindlin plate theory, are presented and they are reduced to a set of ordinary differential equations (ODEs) with time-dependent coefficients using the Galerkin procedure.All inertial components of the moving masses are adopted in the dynamical formulation.Instability survey is carried out for three different loading trajectories considerably interested in many practical applications of the issue,i.e. rectilinear, diagonal and orbiting trajectories. In order to analyze the resonance conditions, the incremental harmonic balance (IHB)method is introduced to calculate instability boundaries, as well as external resonance curves in parameters plane.A comprehensive study is done to assess effects of thickness ratio and foundation stiffness on the resonance conditions.It is found that an increase in the plate's thickness ratio leads to a reduction in values of critical parameters.Moreover,it is observed that increasing the foundation stiffness moves the instability regions and resonance curves to higher frequencies of the moving masses and also leads to further stability of the parametrically excited system at lower frequencies.Time response simulations done via Runge-Kutta method confirmed the results predicted by IHB method.

Keywords Mass-plate interaction·Mindlin plate·Parametric resonance·External resonance·Incremental harmonic balance method

1 Introduction

The vibration problem of solids excited by moving loads is an important academic field with broad industrial applications, e.g., railway tracks and highway bridges under the action of traversing trains or vehicles, machining process of long shafts, and overhead cranes. So, investigation of dynamics of these structures has been a challenging issue for a long time, and hence there is a comprehensive literature review on the dynamic response of elastic beams and plates under moving load/mass excitation, of which a brief survey is presented here.Dynamic behavior and modal control of a simply supported Euler-Bernoulli beam exited by a moving mass were examined by Nikkhoo et al.[1].A study by Yang et al. [2] investigated the dynamic response of a finite Timoshenko beam lying on a six-parameter foundation subjected to a moving load.In his work,Rao[3]studied parametric resonance,as well as internal and external resonance of an Euler-Bernoulli beam excited by moving loads and masses.All acceleration terms of the moving mass were considered and significance of moving mass inertial effects on the results was emphasized. He reported that although the external resonance occurs due to the gravity effects of the moving load,the parametric and internal resonances just depend on the load mass parameter, i.e., ratio of the moving load mass to the beam mass. The work of Pirmoradian et al. [4, 5] investigated instability, external and parametric resonance of Euler-Bernoulli and Timoshenko beams subjected to moving mass loading by Floquet theory and IHB method. The results of the incremental harmonic balance (IHB) method were remarkably close to those of the Floquet theory. They concluded that for a certain value of the moving mass, the Timoshenko beam would resonate at smaller speed values compared with an Euler-Bernoulli beam.Furthermore,Shadnam et al.[6]investigated dynamics of geometrically nonlinear thin plates under influence of relatively heavy moving masses.For the first time,Gbadeyan and Dada [7] used the Mindlin plate theory to study elastodynamic response of a rectangular plate traversed by a distributed moving mass.Considering all acceleration components of the moving mass in the analysis, time history response of the plate's midpoint deflection was found and effects of shear deformation and rotary inertia of the plate on the responses were examined. The work by Wu[8]studied vibrations of an inclined flat plate influenced by traveling loads numerically. He noted that influence of Coriolis and centrifugal forces on the vertical and horizontal displacements of the inclined plate will enhance by increasing the moving loads'speed.In their study,Kiani et al.[9]assessed the dynamic response of multispan viscoelastic thin beams subjected to a moving mass by generalized moving least square method.Also,Nikkhoo and Rofooei[10]performed a parametric study on the dynamic response of thin rectangular plates traversed by a moving mass considering two rectilinear and orbiting paths for the mass trajectory on the plate.Effects of weights and velocities of the moving mass,as well as the plate's aspect ratio on the maximum dynamic response of the plate were examined.Their results indicate that ignoring the inertial effects of the moving mass leads to remarkable erroneous results.The work of Rofooei et al.[11]explored the dynamic response of geometrically nonlinear thin rectangular plates under moving mass excitation. Then Amiri et al.[12]studied vibrations of a Mindlin elastic plate under moving masses by considering diverse paths for the masses.Their results highlight the significance of considering the shear deformation effect in the analyses of moderately thick plates. Another study by Nikkhoo et al. [13] investigated resonance of a single span thin rectangular plate caused by the motion of multiple opposing moving masses.The study by Esen[14]presented a new finite element method to study transverse vibrations of a thin rectangular plate under traversing moving point masses. A similar method was used by Esen [15] to analyze transverse and longitudinal vibrations of thin rectangular plates subjected to a moving load with changing velocity.Orthonormal polynomial series expansion method and eigenfunction expansion method were utilized by Ghazvini et al.[16]to capture the response of a thin rectangular plate with varying thickness under a traveling inertial load.A more complete literature review on the elastic structures under moving masses may be found in Refs.[17,18].

The early studies on the load-structure interaction problem were contrived based on neglecting the inertia of the moving object, known as the moving force problem. In this approach, the external resonance may just happen. By involving the inertial effects of the moving load into the problem,a more precise and severe formulation is revealed,where time-dependent coefficients emerge in the equation of motion and the concept of parametrically excited systems are exposed to discussion.

In contrast to external excitation in which the forcing terms appear as inhomogeneous in the equations of motion,parametric excitation appears as an internal factor leading to self-energizing vibrations of the system [19, 20]. Some common examples of parametrically excited systems are cam follower systems,a pendulum with periodically varying length, and structures such as beams, plates and shells under periodic axial loading. Considerable attention has been dedicated to parametrically excited systems due to the existence of a unique type of resonance, which is called principle parametric resonance. This type of resonance is peculiar because it occurs when the forcing frequency is close to twice that of the natural frequencies of the excited system[21,22].As a consequence of parametric resonance occurrence,the system becomes unstable and its oscillation amplitude increases with time.So,the nature of parametric excitation can be risky to structures.

One of the main objectives of analysing parametrically excited systems is to find their analytical solutions. While there is no analytic solution for most categories of parametrically excited systems,useful properties can be inferred for subclasses comprising periodically varying systems (Hilltype equations). Periodicity of the coefficients results in unique properties enabling one to study stability of these systems with respect to parameter variations, represented as stability diagrams in the plane of system parameters.Based on Floquet's theory, different numerical and semianalyticalmethodsareappliedtodistinguishmultipleregions appearing in the stability diagram [23-26]. The boundaries separating these regions, referred to as transition curves,denote parameter values for which periodic solutions occur.As a generic feature of differential equations with periodic coefficients, instability regions are usually demonstrated in the form of resonance tongues.

A literature survey shows that only a few investigations on the moving load problem are concerned with identifying parametric resonance in such systems[4,5,24]where elastic beams were often considered the supporting structures.Nevertheless,there are some structures subjected to moving loads such as aircraft carriers,slab-type bridges,road pavements and hard disk drives,in which adopting beam models may lead to erroneous results and there is a necessity to use plate theories for their analysis.Plates are two-dimensional structures whose dynamic analyses are generally different and more complicated than those of beams. With regard to parametric resonance conditions of the plate-mass system,recently,Pirmoradian et al.[27]and Torkan et al.[28]investigated dynamic stability of thin rectangular plates under successive moving masses, where non-Mindlin plates were considered in the analyses.With due attention to avoid any failure which may be caused according to happening of instability in related practical structures and also theoretical significance of this concept,the current study is dedicated to analyze dynamic stability of Mindlin plates under the excitation of moving masses.In this article,the woks are as follows.

(1) The formulation of periodic loading of a plate is presented for three different loading paths of moving masses including rectilinear,diagonal and orbiting trajectories.

(2) All inertial effects of the moving masses are considered in the dynamical formulation.

(3) Taking into account the effects of transverse shear deformation and rotatory inertia, the plate is modeled according to Mindlin theory. The error of not employing this theory will demonstrate to be noteworthy in situations where plates with smaller aspect ratio are concerned and may otherwise lead to an erroneous stability criterion.

(4) Incremental harmonic balance method is employed as a semi-analytical method to determine stability diagrams in the plane of system parameters in addition to external resonance conditions.

(5) Effects of thickness ratio and foundation stiffness on the resonance conditions are studied in detail for each loading trajectory.

(6) The instability conditions of the plate-moving force model are inferred as a simplified case of the platemoving mass model.

(7) Based on the Runge-Kutta method,several illustrative examples of the plate time response are presented to confirm the predicted semi-analytical results, wherein all aforementioned trajectories of the moving mass are examined.

(8) Wherepossible,theresultsareverifieduponcomparison with those documented in the literature.

2 Mathematical modeling

Fig.1 a Top view and b side view of a simply supported rectangular plate subjected to a moving mass traveling on an arbitrary trajectory

A uniform,moderately thick rectangular plate with length of a, width of b, thickness of h, traversed by a moving mass M, along an arbitrary trajectory is considered (Fig. 1). The Cartesian coordinate system is assumed so that the origin is at one corner of the plate's midplane,x,y,and z coordinates are taken along the length,width and thickness of the plate,respectively.The plate is embedded in a Winkler-type foundation with constant spring of kw. It is considered that the moving mass travels in contact with the plate at all times.Moreover, all the out-of-plane translational and convective acceleration terms are taken into account to study the inertial effects of the moving mass.The material of the plate is set to be undamped,linear isotropic homogeneous with a Young's modulus of E,flexural rigidity of D,shear modulus of G,and Poisson's ratio of ν.The plate has a uniform mass distribution,i.e.,the plate density,ρ,is uniform throughout the plate.

The coupled differential equations of motion based on the Mindlin plate theory with the consideration of shear displacement and rotary inertia can be written as[29]

where w(x,y,t)is the transverse displacement of the plate at time t, and ψx(x,y,t) and ψy(x,y,t) denote the local rotations about x and y axes,respectively. J =h3/12 is the

rotary inertia of the plate and κ introduces the shear correction factor.Using the Dirac delta function,δ(t),the external excitation force due to a moving mass which travels on an arbitrary trajectory over the plate's surface,may be defined as

where g is gravitational acceleration, and xM(t) and yM(t)represent the location of the moving mass over the plate's surface at time t.Considering all components of the moving mass acceleration,Eq.(4)may be expanded as

According to Eq.(5),the mass acceleration contains nine terms. The first term is from the gravitational acceleration.The second term introduces the local acceleration due to plate flexure. The third to fifth terms signify the coupling of the product of the mass velocities and the plate curvature,which are derived from the centrifugal accelerations.The sixth and seventh terms come from the Coriolis acceleration and represent the coupling of the mass velocities and the time rate of change of plate flexural slope. The last two terms come from the variation of the mass velocities and define the coupling between the mass acceleration and the plate flexural slope. Substituting Eq. (5) into Eq. (1) gives the governing equations as follows

Equations (6)-(8) represent the strong form of the motion equations of amoderatelythickrectangular plateonanelastic foundation subjected to a moving mass.As can be seen,the inertial effects of the moving mass are incorporated into the formulations of the problem.

2.1 Discretization of motion equations

Finding an analytical solution for three coupled Eqs.(6)-(8)is a challenging issue even when simply supported boundaries are considered for all plate edges. Indeed, this is due to the appearance of whole terms of the inertial effects in the dynamical formulation. However, considering all inertial effects of the moving mass in the mathematical model would lead to more realistic and logical equations. Herein,the Galerkin procedure is utilized to solve these equations.Thus,the unknown displacements are discretized in terms of shape functions corresponding to the problem boundary conditions.To develop the discrete form of the motion equations,the transverse dynamic deflection,w(x,y,t),and local rotations ψx(x,y,t)and ψy(x,y,t)are given in terms of shape functions by following expressions

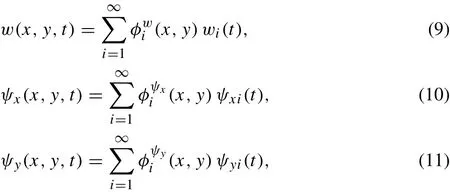
where wi(t),ψxi(t),and ψyi(t)are time-dependent generalized coordinates.Also,φwi(x,y),φψxi(x,y),and φψyi(x,y)are i-th shape functions associated with transverse displacement, and local rotations about x and y directions,respectively.Thetrigonometricshapefunctionswhichsatisfy the simply supported boundary conditions can be expressed as

where m and n are vibrational mode numbers in x and y directions.Substituting Eqs.(12)-(14)into Eqs.(9)-(11),then the resultant equations into Eqs.(6)-(8),then multiplying both sides of Eq.(6)by φwj(x,y),Eq.(7)by φψxj (x,y),and Eq.(8)by φψyj (x,y),and finally integrating over the plate's surface results in the following discrete equations of motion

where the non-zero submatrices are stated as

It is noteworthy that for the case of moving force,the values of parameters appearing in mass,stiffness,and damping matrices of Eq. (15) just depend on the mechanical characteristic of the plate and would result in a set of coupled autonomous equations.On the contrary,for the case of moving mass loading,the inertial effects modify components of the system matrices and so a set of coupled time-varying equations are obtained.

2.2 Rectilinear trajectory

In this section,assuming that the moving mass travels along a rectilinear trajectory parallel to plate boundaries with constant velocity of V, the exclusive equations of this loading pattern are derived. This type of loading trajectory may be considered as a simulation of structural systems such as decks of aircrafts carriers, slab-type bridges under vehicular loading and road pavements.In rectilinear trajectory,the time-varying position of the mass over the plate's surface can be defined as(Fig.2a)

Fig.2 Rectangular plate subjected to a moving mass traveling on a rectilinear trajectory,b diagonal trajectory,and c orbiting trajectory

Substituting Eqs.(17)and(18)into Eq.(15)and assuming the first vibrational mode of the plate, the governing coupled ordinary differential equations (ODEs) of the system are obtained as

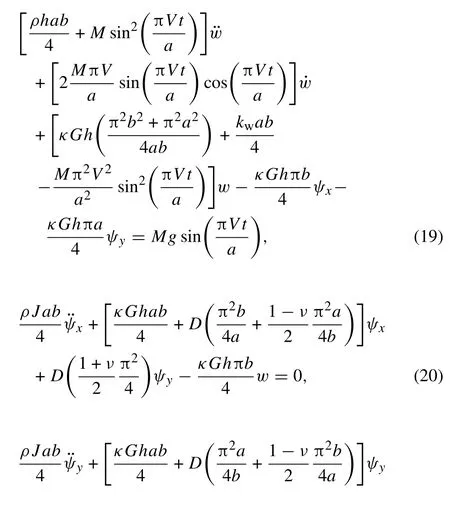
While the mass is on the plate surface (0 ≤t ≤a/V),accordingly the plate is influenced.Obviously,when the mass leaves the plate (t ＞a/V), the parameters associated with the moving mass have to be set to zero(set M =0 in Eq.(19))and the plate would experience a transient free vibration.Hence, in order to analyze the stability of the plate over a long time,it is considered that when a mass leaves the plate the next one enters and goes on,resulting in a parametric-type excitation. Therefore, time-varying coefficients of Eq. (19)become periodic with period T = a/V. So, writing the Fourier expansion of time-varying coefficients of Eq. (19)with period T =a/V,one can come in

In order to obtain general results,introducing the following dimensionless parameters to Eqs.(20)-(22)

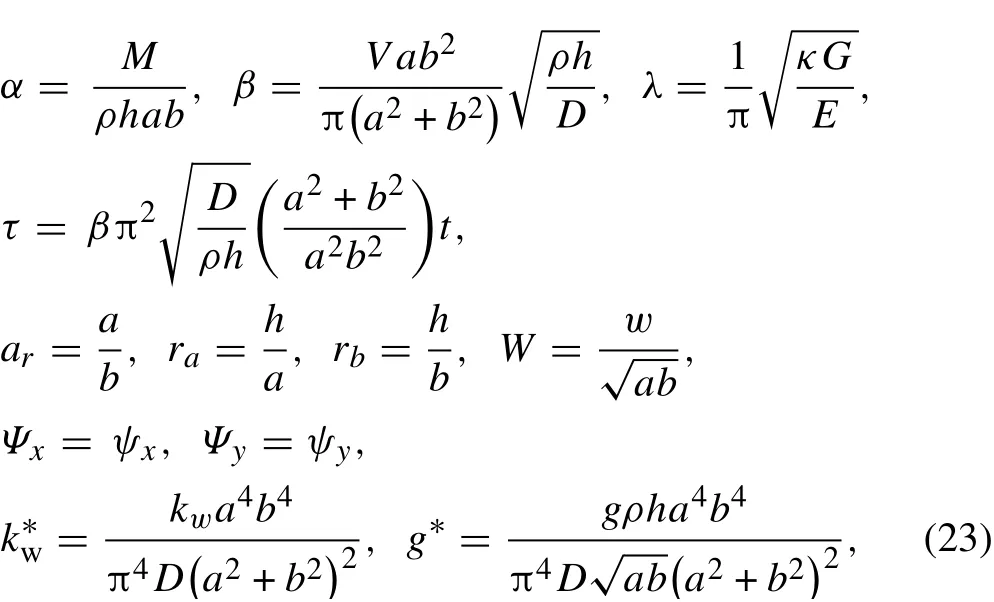
and using the chain rule, the non-dimensional equations of motion of a simply supported moderately thick rectangular plate on an elastic foundation traversed by sequential moving masses along a rectilinear trajectory are derived as

where prime denotes derivative with respect to dimensionless time, τ. Equations (24)-(26) consist of three coupled equations while the first one includes the gravitational acceleration. This term may result in external resonance and therefore unlimited increase in vibration amplitude [3].Moreover,it is noticeable that the moving load inertia terms exhibit the modal Eq. (24) parametrically excited where dynamic instability can occur due to parametric resonance.So,to study dynamic instability due to parametric resonance,the right-hand side of Eq.(15)is momentarily disregarded as follows

2.3 Diagonal trajectory

In this section,to investigate the influence of passage trajectory of moving masses on instability conditions,a diagonal trajectory is considered as shown in Fig.2b.Parametric equations of this trajectory can be described as

Introducing Eqs.(28)and(29)into Eq.(15),the coupled governing equations of a plate subjected to a moving mass traveling along a diagonal trajectory are obtained as

Performing Fourier expansion of coefficients of Eq.(30)with period T =and redefining the following dimensionless parameter

the dimensionless governing equations of the parametrically excited system based on the first-order shear deformation theory are achieved as

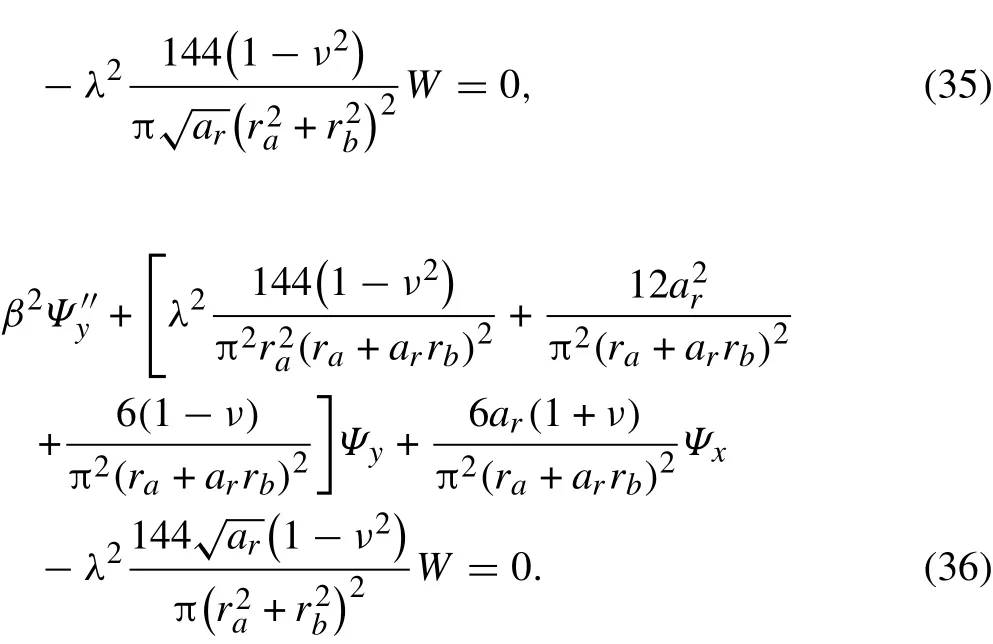
In order to study the instability of the system,disregarding the right-hand side of Eq. (34) leads to the following homogenous ODE

2.4 Orbiting trajectory

Circular motion of a mass on a plate, appearing in some industrial applications such as rotating machineries, computer discs,circular wood saws and vehicle disks,is another path which is studied in this paper.Let the moving mass orbit on a circle with radius r positioned at the center of the plate(see Fig.2c).Considering a constant angular frequency of ω for the mass motion,its position can be described as

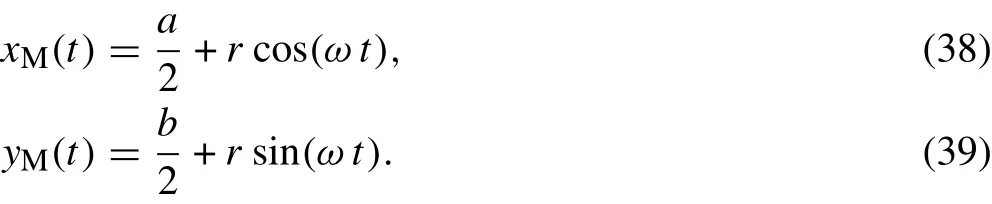
Using Eqs. (15), (38), and (39), the equations of motion in terms of displacement components are derived as

in which

Because of the periodic nature of the mentioned orbiting trajectory,the coefficients of Eq.(40)are periodic with period T =2π/ω and so there is no need to perform Fourier expansion for time-varying coefficients for this loading trajectory.Using the following dimensionless parameters

one can get the following dimensionless coupled equations of motion

in which

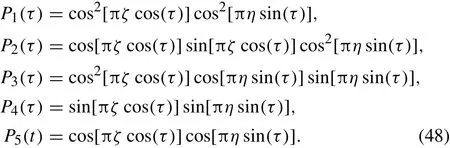
Again, neglecting gravity, the homogenous form of Eq.(45)is considered for further instability analyses as

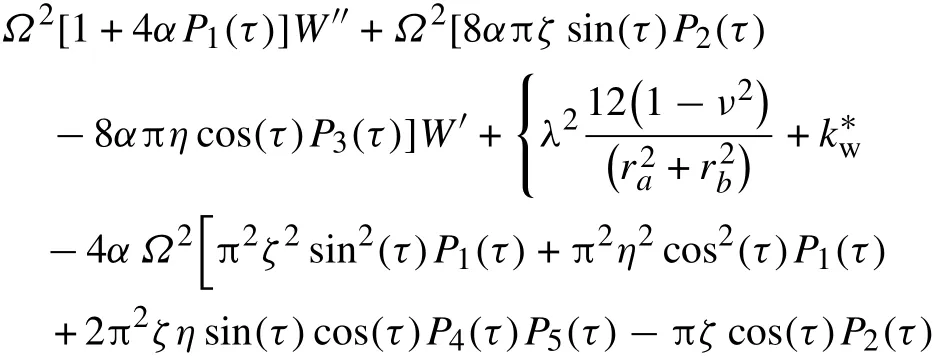
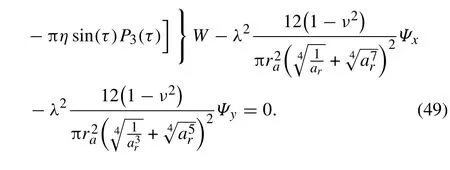
3 Instability analyses and discussions

In this study,comprehensive instability analyses are carried out to find conditions of the occurrence of both parametric and external resonances for the plate-mass system.For this purpose, IHB method is employed to obtain the instability boundaries in parameters plane in addition to external resonance curves. In this method, the periodic solution of the dynamical system is represented by truncated finite Fourier series.Therefore,the governing equations of the system are transformed into a set of linearized incremental algebraic equations in terms of the Fourier coefficients. Then, the Galerkin procedure is applied to these equations and finally an iterative approach is adopted in each incremental step.Compared with numerical approaches such as Floquet's theory[28]and energy-rate method[23]to analyze instability of periodic systems,the IHB method as a semi-analytical tool can predict some phenomena such as coexistence that cannot be justified by numerical methods.Moreover,in comparison withtheharmonicbalancemethod[30,31],whichisasteadystate method and does not consider the initial transients,the IHB method appears to handle strong nonlinearities well by using a Newton-Raphson procedure,and provides accurate solutions over a much broader range since it accommodates multiple harmonics.

3.1 Parametric resonance conditions

The first step of the IHB method is a Newton-Raphson procedure. Assuming (α*,β*) to be a certain instability boundary point corresponding to a periodic solutionthen a neighbor boundary point may be defined as

where Δ Q(τ),Δα and Δβ are small increments.Inserting Eq.(50)into Eqs.(25-27),and omitting the nonlinear terms of the small increments results in

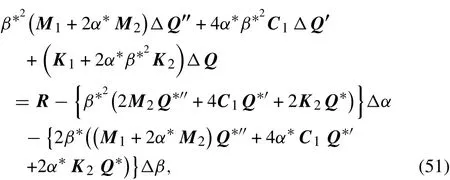
in which

and

When the values of Q*(τ),α*and β*tend to the exact solutions,the corrective term R tends to zero.

Expanding Q*and Δ Q in a truncated finite Fourier series and applying the Galerkin procedure,an approximate solution will be obtained.The periodic solution of period T can be taken as

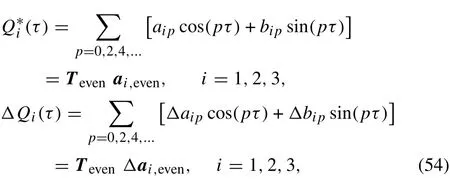
in which

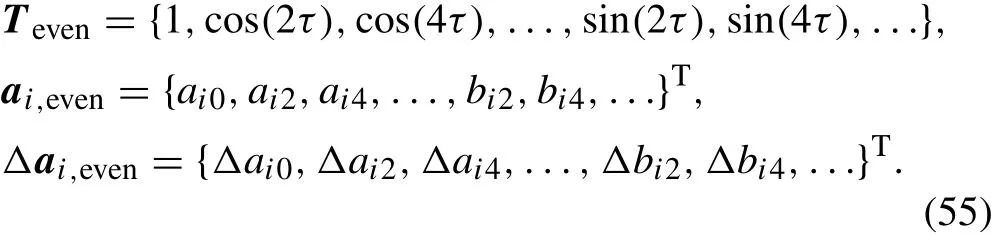
Also,for a periodic solution with period 2T, Q*and Δ Q can be expanded as

in which

So Q*and Δ Q can be written in their terse form as follows

where

In Eqs.(55)and(59),based on the fact that when one of the T-period or 2T-period solutions has to be found,the corresponding T,aiand Δaiare selected.

Applying the Galerkin procedure on Eq. (51) for one period,one can arrive at

At last,substituting Eq.(58)into Eq.(60),a set of linear equations in which ΔA, Δα and Δβ are unknown can be obtained in the following matrix-vector form

in which

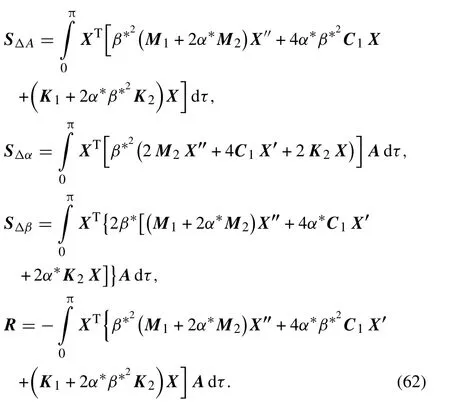
The unknown terms are two more than the number of equations in Eq. (61). Hence, by selecting α as an active parameter and setting its increment Δα equal to zero, and also setting the i-th element of ΔA equal to zero,the number of unknowns and equations are already the same and they can be solved.Now,β*and A are found through the following iterative algorithm:

(1) Select α*.

(2) Select initial values for β*and A.

(3) Solve the following linear equation:wherethe modified form of SΔAby eliminating its ith column and Δ¯A is the changed form of vector ΔA by removing its i-th element.

(4) Check convergence of the solution by examining‖R‖≤ε,where ε is the convergence parameter.

(5) Update β*and A as=β+Δβ and Anew= A+ΔA if it is required,and repeat the procedure from step(3)if convergence is not reached.

(6) Select a new value for α*and repeat steps(1)-(5)to find corresponding values for β*and A.

In fact,the IHB method calculates those parameters of the moving masses in β -α plane. which gives periodic solutions for coupled Eqs.(25)-(27).These particular parameter values create some transition curves in the stability diagram,which separate stable and unstable regions.When two transition curves originate from the same point on the β axis,they form an instability interval,which is referred to as parametric resonance tongue.It is known from Floquet's theory that for an equation with periodic coefficients of period T,the solutions on the transition curves will be periodic with period T or 2T. The first resonance tongue surrounded by 2T-period curves is usually the most important in the study of structures and is identified as principle resonance tongue[22].This is because the first resonance tongue is wider than other resonance tongues.

The instability boundary associated with a periodic solution of period T for a simply supported moderately thick rectangular plate traversed by sequential moving masses along a rectilinear path is shown in Fig. 3. The parameters have been selected as ν = 0.3, κ = 5/6, k*w= 0,ar= 1, and ra= rb= 0.15. In the analyses, the convergence parameter is considered ε = 10-5. As shown,the regions above and below the boundary display unstable and stable behaviors, respectively. Moreover, Fig. 3 shows that for a larger mass ratio, instability occurs for a wider range of the mass transition frequencies.In addition,different numbers of harmonic terms of Eq.(54)were considered to check the convergency in Fig. 3. As depicted, results of the three-and four-term expansions converge.Therefore,for the rest of the paper,the analyses are performed by considering three-term harmonics of truncated Fourier expansions of Eq. (54) or (56). Other instability boundaries associated with the periodic solutions of period 2T are plotted in Fig.4 besides the T-period curve.Indeed,in Fig.4,two boundary curves corresponding to sine and cosine periodic solutions of period 2T,which should define a principle resonance tongue,coincide and consequently produce a zero-thickness instability tongue. Existence of a tongue of zero-thickness implies occurrence of coexistence phenomenon in the plate-mass system for the rectilinear path of masses transition.This can be interpreted as the common occurrence (coexistence) of two independent solutions for the same pair of parameters lying on this curve.More detail of this phenomenon and its importance in engineering design were reported by Karimpour et al.[24]in the study of beam-mass interaction.

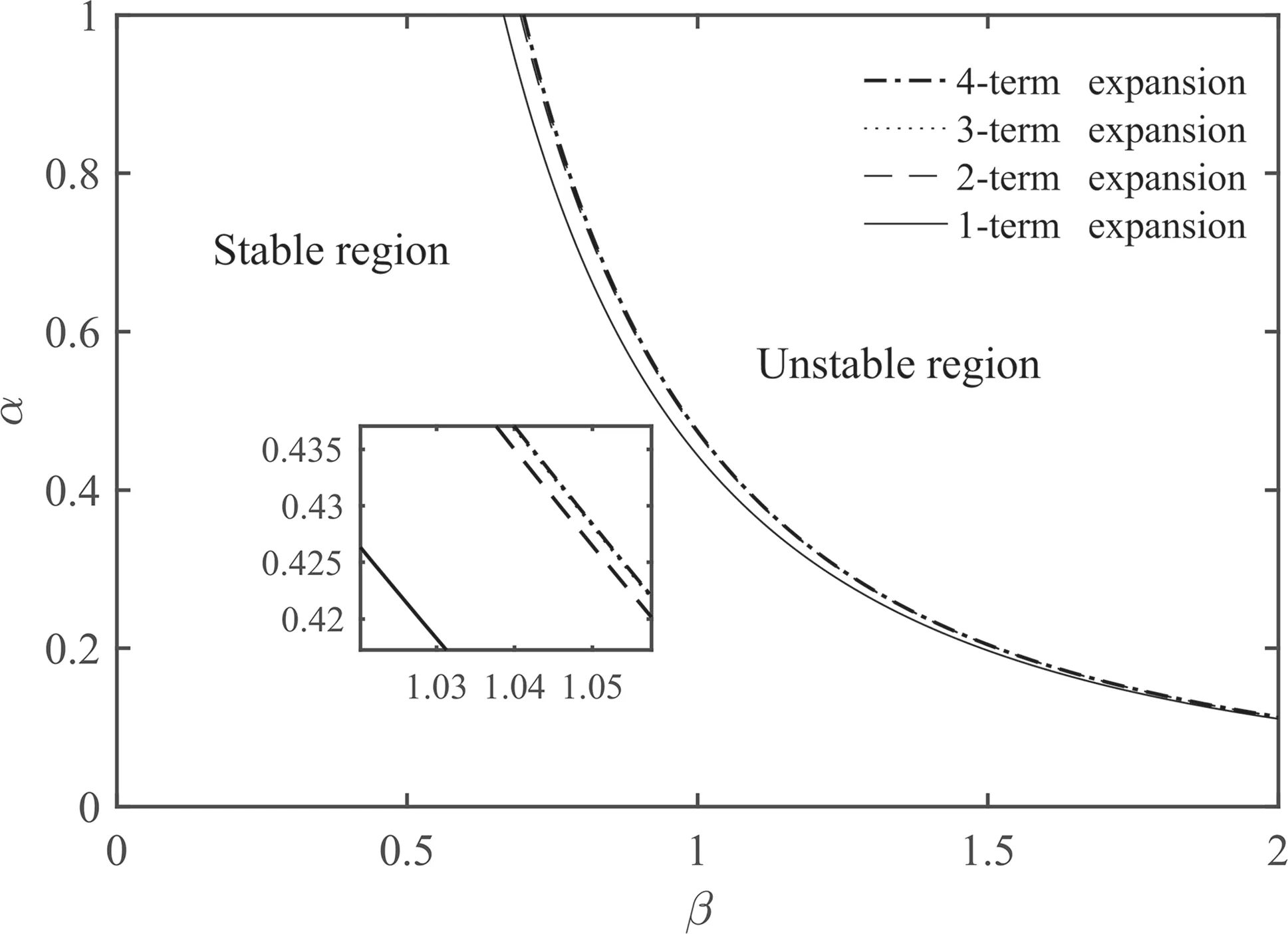
Fig.3 Instability boundary in the parameters plane related to rectilinear trajectory

Fig.4 Instability boundary and coexistence curve in the parameters plane related to rectilinear trajectory

Performing a process similar to that was done for the rectilinear trajectory,the semi-analytical results for the diagonal trajectory are obtained and presented in Fig.5.It can be seen that for this case of loading trajectory, in addition to stable and unstable regions there exists a principle resonance tongue,which is surrounded by 2T periodic solution curves.From Figs.4 and 5,it can be seen that by increasing the mass ratios,α,the critical velocities,β,will decrease.Moreover,comparing Figs.4 and 5 shows that for the diagonal trajectory, the unstable region has spread. Also, the coexistence curve has opened up and so the curves associated with periodic solutions of period 2T are not coincident and they form an instability tongue in the case of diagonal trajectory loading. From a practical point of view, these results show that the trajectory of moving masses over the plate's surface has a great significance on the parametric resonance conditions.

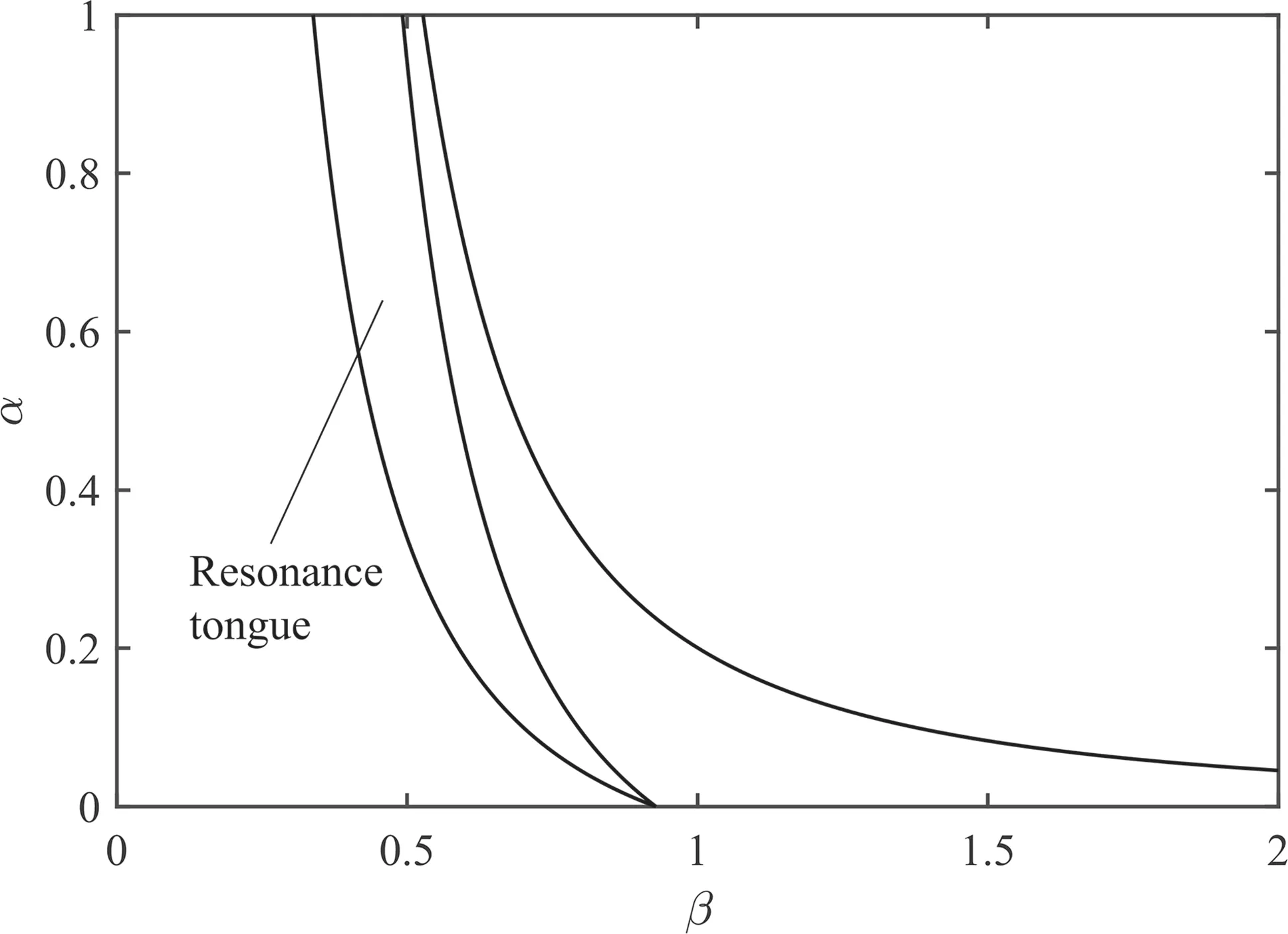
Fig.5 Instability boundaries in the parameters plane related to diagonal trajectory

The results of instability analyses can be verified by calculating the time responses of transverse deflections.For this purpose,Eqs.(24)-(26)and(34)-(36)are solved for points(β =0.6478, α =0.3) and (β =1.15, α =0.3) using the Runge-Kutta method.These two sets of parameters for the case of rectilinear path are located on the coexistence curve and the stable region, respectively, but they belong to the instability tongue and the unstable region for the case of diagonal trajectory. In these analyses the numerical values of the system parameters are chosen as ν = 0.3,κ = 56,= 0, ar= 1, and ra= 0.15. The time responses for point (β =0.6478, α =0.3) are plotted in Fig. 6. As shown in Fig. 6a, the time response of the plate is periodic and bounded for the selected parameters in the case of rectilinear trajectory. However, it can be observed from Fig.6b that in the case of diagonal trajectory the amplitude of time response increases with time. Also, time responses for point (β =1.15, α =0.3) illustrated in Fig. 7 confirm that vibrational behavior of the plate is in agreement with those predicted by the semi-analytical results.

As mentioned before,orbiting trajectory is a more different loading pattern considered for the path of mass motion on the plate.Stability diagrams are established for this loading pattern by performing algorithm of IHB method on three coupled Eqs. (46), (47), and (49). It should be noted that Eq. (49) includes some time-varying terms such as p1(τ), p2(τ),...,p5(τ)that calculating their integral analytically during the IHB procedure is not possible, so it is necessary to substitute these terms by the following Bessel functions

Fig.6 Time responses of the plate for point (β =0.6478, α =0.3).a Rectilinear trajectory.b Diagonal trajectory

Fig.7 Time responses of the plate for point(β =1.15,α =0.3).a Rectilinear trajectory.b Diagonal trajectory

Fig.8 Instability boundaries in the parameters plane for orbiting trajectory

where Jn(x) n = 1,2,...are Bessel functions of n kind.The instability regions for a simply supported moderately thick rectangular plate subjected to a moving mass which travels along an orbiting trajectory are shown in Fig.8 with the following dimensionless parameters:ν = 0.3,κ = 5/6,k*w= 0,ar= 1,ra= 0.15,and ζ = 0.15.As can be seen,in this case of loading pattern the T-period curve separates stable and unstable regions at high frequencies of the orbiting mass motion.However,a principle resonance tongue has appeared in Ω-α plane,which cannot be ignored.Although considering more harmonic terms of Eq.(64)in the analyses will eventuate in more accurate results,through the complexity of governing equations of orbiting trajectory and high numbers of computation in IHB method, the analyses time increases sharply.Hence,Fig.8 has been presented to investigate the effect of considering different number of harmonic terms of Eq. (64) on the transition curves. It is clear that the accuracy of one-term expansion results is not enough especially for the T-period curve,while results of three-and four-term expansion converge and provide good precision.

The influence of relative radius,ζ,on the stability diagram has been investigated in Fig. 9. As shown, the area of the instability regions is broadened by increasing the radius of mass motion. This means that for a larger radius, the plate vibrations become unstable for a wider range of masses and frequencies of the orbiting load.

Figure 10 shows time responses of the plate for different parameters picked from parametric regions of Fig.8.A good agreement with the results predicted by the IHB method can be seen.For example, Fig.10a depicts a bounded response for parameters (Ω =3.9, α =0.7) selected from the stable region of Fig. 8 in the neighborhood of the boundary.However, Fig. 10b shows that the amplitude of transverse oscillations of the plate increases exponentially by time when the values of Ω and α belong to the unstable region, i.e.,(Ω =4.1, α =0.7). Figure 10c shows unbounded oscillatory response of the plate for parameters(Ω =0.6, α =0.7)belonging to the principle resonance tongue of Fig.8,where the parametric resonance leads to instability of the plate's transverse vibrations.

Fig.9 Effect of radius of mass motion on the instability regions.a ζ =0.25.b ζ =0.35

The effect of plate's thickness ratio,ra,on the instability regions of the plate-mass system is shown in Fig.11 for all cases of loading trajectories. As a matter of fact, when the thickness of the plate relative to its in-plane characteristic dimension is less than 0.02, i.e., h/a ≤0.02, the plate is classified as a thin one[32],in which the shear deformation effect is negligible.As shown in Fig.11a,for rectilinear trajectory, decreasing the thickness ratio moves the transition curve toward the right, and consequently the width of the unstableregiondecreases,especiallyforheaviermasses.This isbecausetheMindlintheoryconsidersmoreflexibilityofthe moderately thick plate compared to thin ones by accounting for shear deformation and rotary inertia effects.Figure 11b,c illustrates effect of thickness ratio on the unstable region and principle resonance tongue for the case of diagonal and orbiting trajectories,respectively.As would be expected,for a specified mass of α, a decrease in ramoves the T-period curve and the resonance tongue to higher frequencies of the moving mass transition.

Fig.10 Time responses of the plate for orbiting trajectory of the mass for points,a(Ω =3.9,α =0.7),b(Ω =4.1,α =0.7),and c(Ω =0.6,α =0.7)

The effects of dimensionless foundation stiffness parameter,k*w,on the parametric regions for all cases of trajectories are shown in Fig. 12 for following parameters, ν = 0.3,κ =5/6,ar=1,ra=0.15 and the relative radius ζ =0.15 for the orbiting trajectory.This figure reveals that for all loading trajectories,by increasing the dimensionless foundation stiffness parameter,both the T-period curve and the principle resonance tongue are shifted toward higher frequencies of the moving mass,and as a result,for a certain mass of the moving load,the occurrence of resonance is delayed.These results show that for related practical applications,selecting appropriate intensity of the foundation stiffness is essential to avoid instability of the system.

3.2 External resonance conditions

In this section,the conditions for external resonance occurrence in the plate-mass system are investigated, which are revealed as the appearance of multiple resonance curves in the stable region. In fact, selecting parameters on these curves provides situations that the plate's oscillation magnitude increases wildly.For time-invariant systems,external resonance occurs when the frequency of the excitation term is close to the natural frequency of the system. Here, for the presented time-varying systems, equating the external excitation frequency appearing in the right-hand side of the governing equations by the frequency of periodic response of the corresponding homogeneous problem,the conditions for the occurrence of external resonance are examined.

Fig.11 Effect of thickness on the instability regions.a Rectilinear trajectory.b Diagonal trajectory.c Orbiting trajectory

According to right-hand side of Eq.(24),considering the following periodic solution for the plate response matched by the first excitation term

Fig.12 Effect of dimensionless foundation stiffness parameter on the instability regions. a Rectilinear trajectory. b Diagonal trajectory.c Orbiting trajectory

Fig.13 Resonance curves in the stable region for rectilinear trajector y

Fig.14 Resonance curves in the stable region for diagonal trajectory

and following the IHB algorithm, the external resonance curve associated with the first excitation term can be established.Since the inhomogeneity of Eq.(24)includes infinite cosine harmonic terms with even frequencies, considering solutions corresponding to other excitation terms,further resonance curves can be determined. The first four resonance curves for the simply supported moderately thick rectangular plate acted by successive masses moving on the rectilinear trajectory are plotted in Fig. 13 for parameters ν = 0.3,κ = 5/6, k*w= 0, ar= 1, and ra= 0.15. The righthand side of Eq. (34) (diagonal path) contains harmonic terms with different frequencies.Also,according to Eqs.(45)and (64), it can be observed that for the case of orbiting path, the inhomogeneity contains infinite number of harmonic terms. Resonance curves for diagonal and orbiting trajectories are depicted in Figs.14 and 15,respectively,by taking into account parameter ζ =0.15 for the orbiting trajectory. These figures predict that for a certain value of α,there exist multiple mass transition frequencies for which the plate experiences resonance and its vibrational amplitude increases with time.

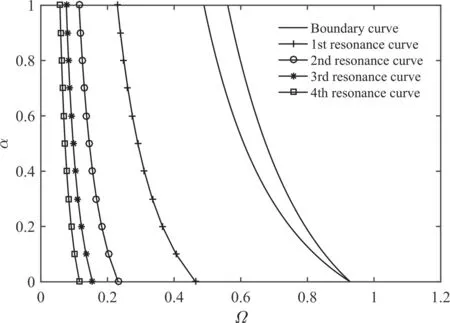
Fig.15 Resonance curves in the stable region for orbiting trajectory

In order to check the validity of these curves,time histories and fast Fourier transform (FFT) of time responses are investigated for numerical values β and α located on the resonance curves. Figure 16a,c, e illustrates unbounded oscillatory response of the plate under rectilinear masses transition for parameters (β =0.4, α =0.3441), (β =0.4, α =0.1806), and(β =0.4, α =0.1227) selected from the 1st, 2nd, and 3rd resonance curves,respectively.Moreover,frequency spectra plotted in Fig.16b,d,f show that the frequency of responses is synchronized with those of external excitations.Similarly,in order to examine the reliability of resonance curves corresponding to diagonal and orbiting trajectories, numerical simulations are performed as shown in Figs. 17 and 18. It can be seen that there exists a good agreement between the numerical and semi-analytical results.

Figure 19 compares resonance curves for a thick plate(ra= 0.15) and a thin plate (ra= 0.02) for all loading trajectories.As shown,by decreasing the value of thickness ratio,the resonance curves shift to right(higher frequencies of the mass transition), which means that considering the classic plate theory overestimates the critical frequencies of the mass transition,especially when smaller plate's thickness ratio values are regarded.

Finally,the influence of foundation stiffness on the resonance curves is presented in Fig.20 for all cases of loading trajectories. As expected, an escalation in the stiffness of Winkler foundation leads to an increase in the mass transition frequencies and from a physical point of view,the proposed system becomes more stable. This allows us to change the resonance frequencies without changing other material and geometrical parameters of the plate.

Fig.16 Time responses and frequency spectra of the plate under rectilinear masses transition for parameters, a, b (β =0.4,α =0.3441),c,d(β =0.4,α =0.1806),and e,f (β =0.4,α =0.1227)located on the 1st,2nd,and 3rd resonance curves,respectively

4 Validation study

In order to validate the semi-analytical results for the simply supported moderately thick rectangular plate exited by moving masses,the obtained results of rectilinear and orbiting trajectories are compared with those reported by Amiri et al.[12]and Torkan et al.[28],respectively.As mentioned,when h/a ≤0.02,the rotation functions ψxand ψyshould approach the respective slopes of the transverse deflection,and consequently the results of applying first-order shear deformation theory should tend to those of classic plate theory. Accordingly, by considering thickness ratio, ra, equal to 0.02 and setting other parameters as ν = 0.3, κ = 5/6,k*w= 0, and ar= 1, some resonance frequencies related to different values of α are compared with the results of Ref. [28] where the classic plate theory was adopted in the analyses (Table 1). A comparison between the results indicates the validity of the present work.

For the case of orbiting trajectory,a comparison is made between external resonance frequencies of the present study and the results of Ref.[12]as shown in Tables 2 and 3 with parametersν =0.3,κ ==0,ar=1.InTable2,the mass ratio and thickness ratio are adopted as α =0.1 and ζ = 0.2,respectively.The comparative study is carried out for different values of thickness ratio.However,in Table 3,by setting ζ =0.3 and ra=0.1,the resonance frequencies are obtained for different mass ratios.A very good agreement is observed from Tables 2 and 3.It is worth mentioning that the results given in the tables have been achieved from the 2nd resonance curve, which is caused by the second excitation frequency.

5 Conclusions

Withintheframeworkoffirst-ordersheardeformationtheory,dynamic instability due to parametric and external resonances of simply supported moderately thick rectangular plates resting on elastic foundations under moving mass excitation was investigated. The governing partial differential equations of motion were discretized using the Galerkin procedure.Three loading trajectories for the motion of masses over the plate's surface were considered including rectilinear, diagonal and orbiting trajectories. The method of IHB was employed to determine instability regions and external resonancecurvesintheparametersplane.Thenumericalsimulations were used to study the reliability of semi-analytical results obtained by IHB method.The results of the instability survey led to some conclusions as follows:

Fig.19 Comparisonoftheresonancecurvesforthethickandthinplates.a Rectilinear trajectory.b Diagonal trajectory.c Orbiting trajectory

Fig.20 Effect of dimensionless foundation stiffness parameter on the resonance curves. a Rectilinear trajectory. b Diagonal trajectory.c Orbiting trajectory

(1) For the rectilinear trajectory,it is found that there is an instability tongue with zero thickness,which is evidence that the coexistence phenomenon occurs.However,for the diagonal trajectory this zero-thickness instability tongue is opened up and forms a wide resonance tongue in the instability diagram. Therefore, the trajectory of periodic transition of moving masses has a great practical significance in the design of related structural systems.

Table 1 Comparison of external resonance frequencies of the plate under successive moving masses for different mass ratios

Table 2 Comparison of external resonance frequencies of the plate under an orbiting mass for different thickness ratios

Table 3 Comparison of external resonance frequencies of the plate under an orbiting mass for different mass ratios

(2) For the orbiting trajectory,results show that the instability regions are broadened as the radius of mass motion increases.

(3) For all cases of loading trajectories there exist multiple external resonance curves in the stable region which cannot be ignored in associated applications.Also,it is reported that decreasing the plate's thickness ratio shifts the critical frequencies of moving masses transition to higher values.

(4) It is shown that an increase in the foundation stiffness leads to a wider stable region of the moderately thick rectangular plate under moving masses.