基于Hebbian规则的新型自适应广义主元分析算法

高迎彬，孔祥玉，崔巧花，董海迪

（1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.火箭军工程大学导弹工程学院，陕西 西安 710025；3.海军工程大学兵器工程学院，湖北 武汉 430033）

1 引言

广义主元是指2 个信号的自相关矩阵构成矩阵束的最大广义特征值所对应的广义特征向量，而广义主元分析是指能够对广义主元进行估计的技术[1]。广义主元分析已经应用在通信和信号处理的很多领域，如盲分离[2]、波束形成器[3]、阵列天线[4]、模式识别[5]、滤波器设计[6]等。针对矩阵束广义特征值分解（GEVD,generalized eigenvector decomposition），学者们提出了一些代数方法来计算信号的广义主元，然而这些代数方法本质上属于批处理类算法，不仅计算复杂度高，而且要求矩阵束是已知的。而通信和信号处理的很多领域中，天线和传感器只能接收当前时刻信号的采样值，自相关矩阵束是未知的，因此有必要发展自适应广义主元分析算法。

利用神经网络对广义主元进行自适应估计是常用的方法。Mathew 等[7]提出含有Sigmoid 激励函数的非线性反馈型神经网络结构，然而该神经元结构过于复杂，需要选取很多参数，不利于实际应用。Hebbian 在研究神经网络学习规律时指出：神经网络权值的更新应该与输入和输出的相关性成正比，进而提出了Hebbian 规则[8]。Oja[9]首次将Hebbian规则引入自适应特征值分解算法领域。相比批处理代数算法和反馈型神经网络算法，基于Hebbian 规则的算法具有以下3 个方面的优势：1)只利用信号当前值来估计广义主元，不需要计算自相关矩阵，算法的实时性较好；2)适用于处理平稳信号和非平稳信号，应用范围广泛；3)计算复杂度相对较低，能够处理高维数据[10]。因此，基于Hebbian 规则的算法已经成为该领域的主流研究方向。

在基于Hebbian 规则的广义主元分析算法方面，Chatterjee 等[11]构建了一个双层线性神经元，并基于此提出了梯度性算法，然而该算法难以选择合适的学习步长。为了避免矩阵的求逆计算，Liu等[12]提出了RNN（recurrent neural network）算法，但该算法存在收敛速度慢的问题。为了提升算法的收敛速度，Tanaka[13]将广义主元转化为特征值分解问题，利用幂迭代法对广义特征向量进行在线估计，然而该算法中存在较多的矩阵开方操作，由于矩阵开方结果的不唯一性使算法的稳定性较差。Nguyen 等[14]则通过对神经元权向量不断地归一化来提升算法的稳定性，但是频繁的归一化操作又增加了算法的计算复杂度。Li 等[15]将Douglas 特征值分解算法扩展到GEVD 领域，提出了没有权向量模值归一化操作的GDM（generalized Douglas minor）算法。目前，广义主元分析算法大多采用加权指数遗忘窗法对自相关矩阵进行在线估计，但该方法往往增加算法的计算复杂度，因此如何有效降低算法的计算复杂度是一个值得研究的课题。

基于Hebbian 学习规则，Möller[16]提出了一种稳定的特征值分解算法。本文通过对该算法进行分析改进，提出了一种新型广义主元分析算法（简称“本文算法”）。本文主要工作如下：1) 采用瞬时近似法进行自相关矩阵估计，有效降低了算法的计算复杂度；2) 通过Lyapunov 稳定性理论对本文算法的稳定性进行分析，证明了本文算法的有效性。

2 GEVD 基础理论

假设存在2 个n维信号向量序列{x(k)∈Rn×1}和{y(k)∈Rn×1}，其自相关矩阵分别为Rx=E[x(k)xT(k)]和Ry=E[y(k)yT(k)]。显然，自相关矩阵Rx和Ry是2 个正定的Hermitian 矩阵。将Rx和Ry组合成矩阵束(Ry,Rx)，则GEVD 问题就是计算n维非零向量p和标量λ，使式(1)成立。

其中，p和λ分别表示矩阵束(Ry,Rx)的广义特征向量和广义特征值。显然对于任意非零常数a，ap也是矩阵束(Ry,Rx)的广义特征向量。为了方便后续使用，这里将矩阵束(Ry,Rx)中关于Rx正交、且模值为1 的广义特征向量vi和对应的广义特征值组成特征对(λi,vi)，其中i=1,2,… ,n。进而根据GEVD的性质，有

其中，i,j∈{1,2,…,n}，δij为Kronecker 函数。

将矩阵束(Ry,Rx)的所有广义特征值按照从大到小的顺序进行排序，即

所对应的广义特征向量也相应调整，则广义特征值λ1对应的广义特征向量v1是信号的广义主元。

3 本文算法的提出

为了自适应地估计信号的广义主元，本文考虑式(4)所示的Hebbian 线性神经元模型。

其中，h(k)∈Rn×1表示神经元的输入，w(k)∈Rn×1表示神经元的权向量，g(k)表示神经元的输出。利用Hebbian 神经元进行广义主元估计是为了构造合适的权向量更新规则，使权向量在经历若干次迭代计算后能够收敛到信号广义主元的方向。

基于式(4)所示的神经元模型，通过对Möller算法[16]进行改进，本文提出了一种新型广义主元分析算法，其数学模型如式(5)所示。

其中，z1(k)=yT(k)w(k)和z2(k)=xT(k)w(k)分别表示神经元的输出，η表示算法的学习因子。通过分析计算可得本文算法的计算复杂度为4n，而文献[17]为10n2+6n，文献[18]为15n2+8n，文献[15]为9n2+4n。显然，本文算法的计算复杂度最低。

对式(5)等号两侧同时取数学期望可得

对比式(5)和式(6)可得，本文算法（式(5)所示）利用自相关矩阵的瞬时估计值来代替矩阵Rx和Ry，虽然该近似操作存在一定的误差，但是通过设计合理的更新学习规则可以保证算法最终的收敛方向[16]，通过该近似操作可以大幅提升算法的实时性，有利于算法的实际应用。此外，通过对比本文算法和现有算法[11-15]可以发现：本文算法与现有算法都是基于Hebbian 规则而提出的，且算法的模型基础是相同的，主要区别在于现有算法采用指数加权遗忘法来对自相关矩阵Rx和Ry进行在线估计，而本文算法则采用信号当前采样值对自相关矩阵进行瞬时估计。由于瞬时估计不需要矩阵相乘操作，节省了很大的计算量，因此本文算法具有较低的计算复杂度。

4 稳定性分析

本节将重点研究算法的稳定性，即分析本文算法中权向量能否准确地收敛到信号广义主元的方向。该分析过程将通过如下2 个定理来完成。

首先基于随机近似理论，本文算法（式(5)所示）的确定性连续时间系统可以表示为

根据数学分析理论，式(7)只能在平衡点处取得稳定状态，因此首先给出式(7)的所有平衡点。

定理1对式(7)而言，S={0,a1v1,a2v2,…,an vn}表示所有平衡点构成的集合，其中，i=1,2,…,n。

证明根据平衡点定义，在平衡点处有f(w)=0，即

其中，

显然，式(8)是矩阵束(Ry,Rx)的广义特征值分解方程，且是式(8)的解。此外，令wi=ai vi,(i=1,2,…,n)，并代入式(9)，有

综上所述，本文算法的平衡点集为S={0,a1v1,a2v2,…,an vn}。证毕。

在得到算法的平衡点后，需要确定哪些平衡点是稳定的，由此可以确定算法最终的收敛结果，相关结论由定理2 给出。

定理2在平衡点集S中，当时平衡点a11v是渐进稳定的，而其他的平衡点都是不稳定的。

证明定义向量函数

则g(w) 的Jacobian 矩阵为

其中，I表示单位矩阵。

根据定理1 可得算法的平衡点集为S。首先考虑平衡点w=0 的情况，即

假设J0的特征值为λ，则有

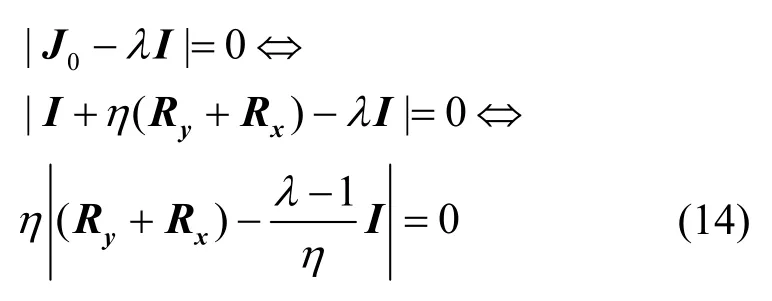
式(14)表明矩阵J0和(Ry+Rx)具有相同的特征向量。令为矩阵(Ry+Rx)的特征值，由于Ry和Rx均是对称正定矩阵，因此矩阵(Ry+Rx)也是对称正定矩阵，其特征值ρ＞0，即J0的特征值λ=nρ+1 ＞ 1。因此根据Lyapunov 稳定性理论可得，平衡点w=0是不稳定的。

接下来，分析wi=ai vi,(i=1,2,…,n}的情况，此时有

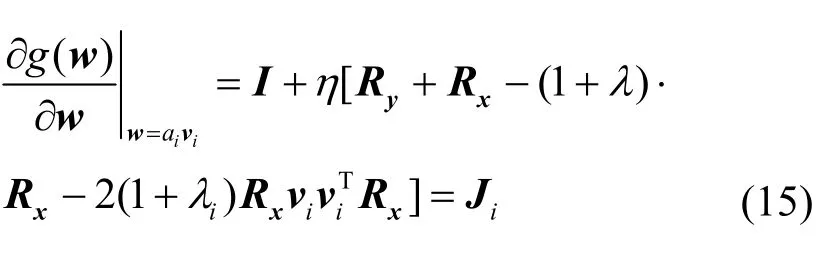
显然，平衡点wi的稳定性是由Ji的谱分析决定的。定义矩阵

则Ji和Mi具有相同的特征向量。Mi分别左乘VT和右乘V，有

其中，Λ′=diag{[0,…,1,… 0]}表示对角线上第i个元素为1、其他元素都为0 的对角矩阵；V表示矩阵束(Ry,Rx)所有广义特征向量构成的矩阵。矩阵的特征值为

根据Lyapunov 稳定性理论，系统渐进稳定的充分条件是对于Ji的任意特征值α，使|α|＜ 1 成立。为便于分析，分别讨论i≠1 和i=1 这2 种情况。

1)i≠1 的情况

当j≠1 时，有

当j=i时，有

当i≠ 1时，始终存在λ1＞λi使式(20)不成立，因此平衡点a2v2,a3v3,…,an vn都是不稳定的。

2)i=1 的情况

当j≠i=1 时，有

当j=i=1 时，有

定理2 表明，本文算法只能在平衡点a11v处取得稳定状态，因此经过若干次迭代运算后，算法的收敛结果必定与矩阵束(Ry,Rx)的最大广义特征值对应的广义特征向量方向相一致，进而证明了本文算法的稳定性。

5 仿真和应用

本节将通过3 个实验来对本文算法的性能进行验证。第一个实验是自相关矩阵束已知情况下，利用本文算法对广义主元进行估计，并与一些现有算法的估计结果进行对比；第二个实验针对自相关矩阵束未知的情况，利用本文算法直接从输入信号中对广义主元进行自适应估计；第三个实验是利用本文算法解决波束形成问题。为了对估计结果进行定量评价，本文采用算法在迭代过程中的方向余弦（DC,direction cosine）作为定量评价指标，如式(24)所示。

方向余弦描述的是权向量与广义主元v1的方向相似度，如果方向余弦值等于1，则表明权向量已经于广义主元v1在方向上重合。

5.1 自相关矩阵束已知情况下实验

利用文献[19]中的方法随机生成式(25)和式(26)所示的正定Hermitian 矩阵。

矩阵束(Ry,Rx)的最大广义特征值λ1=2.695 0，其对应的广义特征向量为

分别采用本文算法（式(6)所示）、RNN 算法[12]和GDM 算法[15]来估计矩阵束(Ry,Rx)的广义主元v1。迭代过程中初始化权向量是随机产生的。图1给出了3 种算法的方向余弦曲线，图2 给出了本文算法在迭代过程中权向量元素的变化情况。

图1 矩阵束已知情况下3 种算法的方向余弦曲线

图2 矩阵束已知情况下本文算法在迭代过程中权向量元素的变化情况

从图2 中可得本文算法的权向量收敛结果为

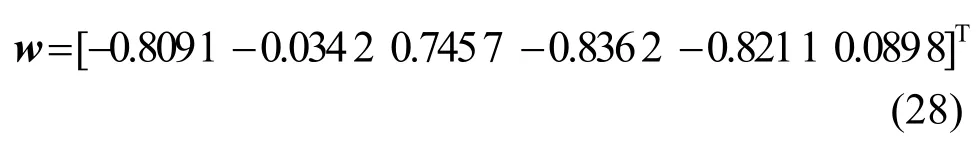
5.2 自适应广义主元估计

这里通过式(29)和式(30)来产生输入信号序列[20]。

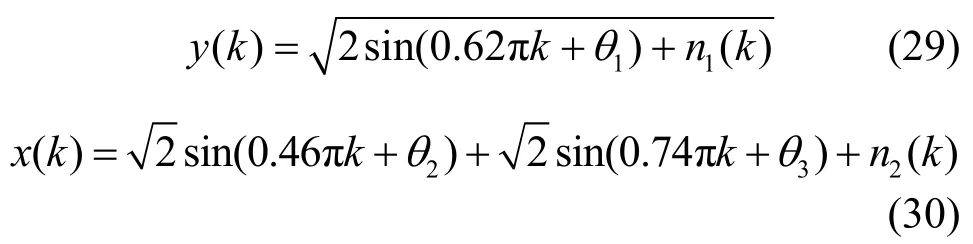
其中，n1(k)和n2(k)表示均值为0、方差为0.1 的加性高斯白噪声，θi(i=1,2,3)表示初始相位且在[0,2π]上服从均匀分布。从式(29)和式(30)中取连续8 个相互重叠的输出作为输入信号向量，即y(k)=[y(k),y(k+1),…,y(k+7)]T和x(k)=[x(k),x(k+1),…,x(k+7)]T。

采用本文算法（式(5)所示）、RNN 算法和GDM算法对随机生成信号的广义主元进行自适应估计，算法中初始化权向量是随机产生的。3 种算法的方向余弦曲线如图3 所示。从图3 中可以看出，在信号自相关矩阵未知的情况下，本文算法通过对自相关矩阵进行瞬时估计，能快速地跟踪并保持在信号的广义主元方向上，而且跟踪速度要优于其他算法。

图3 自相关矩阵未知情况下3 种算法的方向余弦曲线

5.3 在波束形成中的应用

波束形成，又称空域滤波，是现代通信领域的重要内容。波束形成技术的基本思想是通过将天线各阵元输出信号进行加权求和，从而将天线阵列波束导向一个特定方向，使天线在期望波束方向取得最大增益，且尽可能地压制其他干扰信号和噪声。文献[21]指出：波束形成器的最优加权向量是满足式(31)所示的最大信号噪声比准则的解。

其中，Rs=E{s(k)sT(k)}和Rd=E{d(k)dT(k)}分别表示期望信号s(k)和干扰信号d(k)的自相关矩阵。根据广义Rayleigh 商的性质[22]，式(31)的最优解刚好是矩阵束(Rs,Rd)的广义主元。

假设空间中一线性等距天线阵列，阵子数量为12，间距为半波长。期望信号的入射角为0°，其他4 个干扰信号的入射角分别为-30°、-15°、-10°、-20°。信号中噪声为加性高斯白噪声，信噪比为30 dB。采用本文算法对该波束形成器的最优加权向量进行估计，算法初始化权向量仍是随机产生的。

采用本文算法和精准广义主元算法获得的波束模式曲线如图4 所示。从图4 可以看出，主波束在期望的方向上有较强的增益，而其他干扰信号则受到了较大抑制。通过对比实验结果发现，本文算法的估计结果与精准的波束模式曲线效果相差不大，即本文算法能够较好地处理波束形成问题。

图4 波束模式

6 结束语

广义主元分析是通信和信号处理领域内的重要分析工具。本文针对如何从输入信号中自适应地对广义主元进行估计这一问题，提出了一种新型广义主元分析算法。该算法利用神经元权向量不断迭代更新来实现广义主元估计，采用自相关矩阵瞬时估计法有效地降低了算法的计算复杂度，基于Lyapunov 稳定性理论完成了本文算法的平衡点分析。最后通过仿真实验和实际应用实验对本文算法的性能进行了验证，验证结果表明本文算法能够有效地提取信号的广义主元，且速度要优于对比算法。