关于复函数积分中值定理的进一步研究

崔艳，储亚伟，李雯雯，叶薇薇

（阜阳师范大学，安徽阜阳236000）

0 引言

积分中值定理是分析学的重要理论基础，实分析中积分中值定理在许多定理的证明和公式的推导中都有重要的应用。然而由反例［1］表明这个定理在复分析中并不成立，众所周知，复分析中解析函数只能在局部满足类似于实分析的中值定理形式，在整个解析区域上积分中值定理的形式与实分析的积分中值定理形式不同。

近年来，国内外专家学者对复函数积分中值定理的条件、结论进行了大量研究，取得了一系列研究成果［2-6］。文献［2］讨论了区间上连续函数的复积分的中值定理，见引理1。文献［3］讨论了凸区域D内直线段上解析函数的复积分的积分中值定理，见引理2。而文献［4］讨论了积分路径为光滑曲线的复变函数的积分中值定理。

本文在文献［2-4］的讨论的基础上，研究了一种新的积分路径为一般光滑曲线的复变函数的积分中值定理，称之为变形的积分中值定理，并将此解析函数中值定理的结论应用于整函数上，进而得出有关整函数的积分中值定理。

1 引理

引理1设复数a,b(a≠b)，函数f(z)沿[a,b]连续，则存在ξ,η∈[a,b]，使∫(a,b)f(z)dz=[Ref(ξ)+iImf(η)](b-a)。

引理2设函数f(z)是凸区域D内的解析函数，z1,z2是D内的任意两点，则在z1与z2的连线段上至少存在两点ξ,η使(z1-z2)。

引理3设C:z=z(t)（a≤t≤b）为区域D内的光滑曲线，φ(z)是区域D内单叶函数，ω=φ(z)将C映成曲线Γ，则Γ是光滑曲线。

2 主要结论

定理1设C:z=z(t)是（凸）区域D内光滑曲线段C:z=z(t),a≤t≤b，φ(z)是区域D内单叶函数，且ω=φ(z)将C映成曲线Γ，如果函数f(ω)沿曲 线Γ连 续，则 一 定 存 在ξ,η∈C，使 得

证明：因为φ(z)在区域D内单叶解析，ω=φ(z)将区域D内光滑曲线C:z=z(t),a≤t≤b映成曲线Γ，根 据 引 理1知Γ是 光 滑 曲 线，从 而

由 于Ref(φ(z(t)))φ'(z(t))和Imf(φ(z(t)))φ'(z(t))均满足实分析中积分中值定理的条件，所以一定存在使 得因此，有

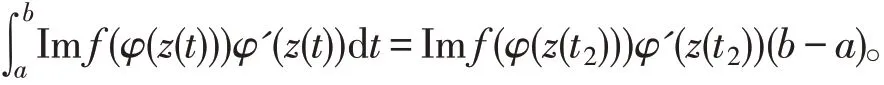
其中ξ=z(t1),η=z(t2)，证毕。

注：当光滑曲线段C是以α为起点β为终点的直线段时，定理1即为文献［4］中结果，文献［4］的局限性在于积分路径是通过单叶函数将直线段映为曲线段，本文将直线段推广为曲线段，极大地拓展了定理的适用范围，直接推广了文献［4］中的相应结论。当φ(z)=z时，定理1即为引理2，又当φ(z)=z并且区域D为[a,b]（a,b是复数），定理1即为引理1，而文献［2，3］结论为本文的两种特殊情形。

整函数是一种重要的解析函数，将积分中值定理1应用于整函数，从而得出关于整函数的一种积分中值定理。

3 整函数的积分中值定理

定理2设φ(z)是单叶整函数，C:z=z(t),a≤t≤b是复平面内光滑曲线段，且ω=φ(z)将C映成曲线Γ，如果函数f(ω)沿曲线Γ连续，那么一定存在ξ,η∈C，使 得

证明：因为φ(z)为整函数，所以φ(z)在全平面内解析，又因为C:z=z(t),a≤t≤b是复平面内光滑曲线段，所以存在原点O的某邻域U(O;δ)，使得z(t)∈U(O;δ)，且使得φ(z)在区域D=U(O;δ)内单叶解析，根据定理1可知结论成立。

4 应用举例

例如，f(z)=eiz，f(z)在整个复平面上解析，且f(0)=f(2π)，我们考虑积分，应用定理2可分别取则成立Re[f(φ(ξ)]φ'(ξ)=

本文成功地将积分中值定理应用范围推广到了积分区域为一般光滑曲线上，并将其应用于整函数情形，这些结论既进一步完善了整个积分学中值定理的内容，同时所蕴含的思想方法也将极大地推动微积分学教学研究工作的开展。