基于FPGA 的高频电力电子装置快速实时仿真数值算法

施 文，迟 颂，郭 亮

（1.河北工业大学电气工程学院省部共建电工装备可靠性与智能化国家重点实验室，天津300132；2.河北工业大学电气工程学院河北省电磁场与电器可靠性重点实验室，天津300132）

以实时仿真为核心的数字双胞胎技术，能够帮助企业在实际投入生产之前在虚拟环境中优化、仿真和测试，实现高效的柔性生产，是企业迈入工业4.0 的解决方案之一， 然而由于宽禁带器件的高频特性使得电力电子装置与数字双胞胎结合的难度增加。 宽禁带器件开关频率可达百kHz，最小稳态时间可低于1 μs，而常见的基于现场可编程门阵列FPGA（field programmable gate array）实时仿真平台RT-LAB、PXI 平台等仿真步长在250 ns 到1 μs 之间[1-2]。过高的开关频率会使得仿真中出现开关时刻偏移等问题，一般采用变步长计算。

文献[3-5]提出了实时仿真并行化的方法，证明了在并行化实时仿真中，可以异步仿真，无须考虑与通讯部分同步， 每部分仿真模型可以将仿真步长减小至算法极限。因此，减少仿真计算时间可以减小仿真步长，有助于在高频下简化开关动作情况，提高仿真精度。算法方面，文献[6-7]利用多步插值的变步长算法，解决了多重开关动作的问题，但算法复杂难以实时计算；文献[8]比较了常用离散迭代算法仿真精度，证明了梯形法综合性能更优；文献[9]使用权重数值积分的方法解决了变步长仿真中的数值发散问题，但都没有涉及实时仿真；文献[10]通过单步插值实现了实时仿真变步长算法；文献[11]通过二阶段积分和自校正单步插值的方法解决了变步长的相关问题，但都未考虑计算时间对仿真步长的影响。

针对现有实时仿真中使用的变步长算法计算速度和数值发散的问题，提出一种基于FPGA 程序结构的实时仿真数值算法，通过改进梯形迭代法以提高算法收敛程度， 在此基础上改进仿真算法结构，使计算更加快速稳定。以三相逆变电路为例，以离线仿真软件精度为标准，对改进算法进行实时仿真，证明算法的有效性。

1 高频电力电子实时仿真存在问题

随着电力电子系统开关频率的不断提高，仿真中会出现开关动作时刻与采样点时刻不一致的情况， 这时开关动作时刻会被归算到采样点时刻，出现开关动作偏移的问题。一般采用变步长算法进行处理，但随之带来了关于数值发散[11]与实时性的问题。 文献[12]总结了变步长算法及适用情况，文献[13]对开关动作偏移问题进行了详细的描述。

（1）数值发散的问题。 由于步长过大或者算法精度不足导致仿真结果发散，通常可以使用高阶迭代算法、多步迭代等方法解决，但在实时仿真中会增加计算时间，进而增大步长，使问题更加复杂，甚至无法保证实时。

（2）实时性问题。 实时仿真最重要的是满足实时性，即：①实时性，步长设定时间等于数据传输间隔时间；②稳定性，最长仿真计算时间小于步长设定时间。

常用的高阶迭代算法会增加总体仿真计算时间，变步长仿真中采用半步长欧拉法仿真增加最长仿真计算时间，从而变相增大了步长。

本文在实时仿真变步长算法的基础上，针对问题（1）提出改进的梯形法以提高收敛性，在此基础上针对问题（2）改进算法计算结构，使计算更加稳定快速，可使仿真步长进一步减小。

2 基于系数控制的数值解算方法

2.1 改进的梯形迭代算法

一般实时仿真主要使用欧拉法迭代配合状态方程对离散电路模型进行求解，公式表示为

其中：第1 式为状态方程，第2 式为欧拉法公式。式中：h 为仿真步长；X 为状态变量；为状态变量的导数；A 和B 为状态方程的数值矩阵； 下标n 代表离散时间点。

欧拉法精度较低， 仿真结果易出现数值发散，可以使用梯形法来提高精度[8-9]。 同样对于状态变量的导数求解使用状态变量法，梯形迭代法公式为

式中，X'为对下一时刻状态变量的预测值。 在实时仿真中，预测计算会延长仿真计算时间，导致仿真步长增大。 通过图1 进行说明。

图1 梯形迭代法计算流程Fig. 1 Calculation flow diagram of trapezoidal iterative algorithm

图1 为梯形迭代法的简化计算流程，其中细箭头表示常数乘法，1/2 表示系数数值，未写数值则系数为1； 而粗箭头代表状态方程AX+B 的计算，最为消耗计算时间，省略了步长h 乘法计算。 梯形迭代法会进行2 次状态方程计算， 存在时序问题，无法并行计算。相比于欧拉法，计算时间增长近1 倍。

为了减少计算时间，对梯形法进行一定改进。图1 中，tn到tn+1中第一次状态方程的计算结果，与tn-1到tn的基于欧拉法的预测计算结果在一定条件下近似等效。 将替换为，可以节省一次状态方程计算，改进的梯形迭代法计算流程如图2 所示。

图2 改进的梯形迭代法计算流程Fig. 2 Calculation flow diagram of improved trapezoidal iterative algorithm

梯形迭代法从tn-1到tn的仿真计算中，存在使用欧拉法对tn的状态变量导数进行预测计算结果，将其运用在tn对tn+1的仿真计算中，如图2 虚线部分所示，整理后得到

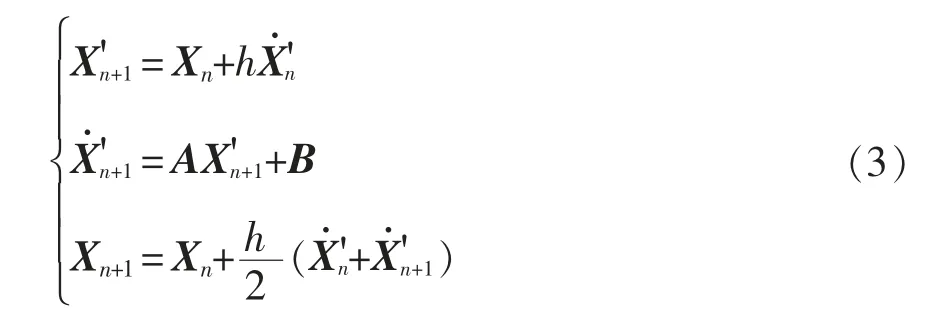
相对于传统梯形迭代法，改进迭代法计算省去一次状态方程的计算，速度更快。

精度方面， 以buck 电路为例对比算法误差进行说明。 电路拓扑如图3 所示。 其中，Es为电源电压，取100 V；电感L 为0.1 mH；负载电阻Rload为2.5 Ω；占空比取0.5；开关频率为10 kHz。对比欧拉法、 改进梯形法与梯形法低步长的仿真结果，以PLECS 仿真结果为标准，计算误差[14]公式为

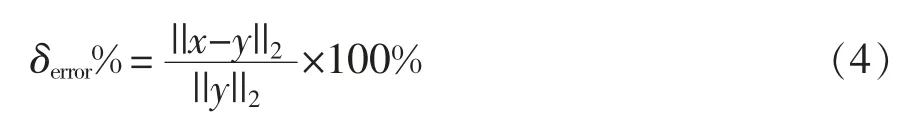
式中：δerror为相对范数误差；x 为标准结果；y 为对比数据。 误差曲线如图4 所示。

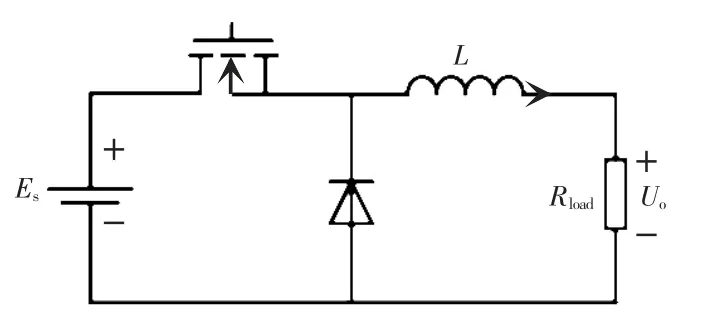
图3 Buck 电路拓扑Fig. 3 Topology of buck circuit

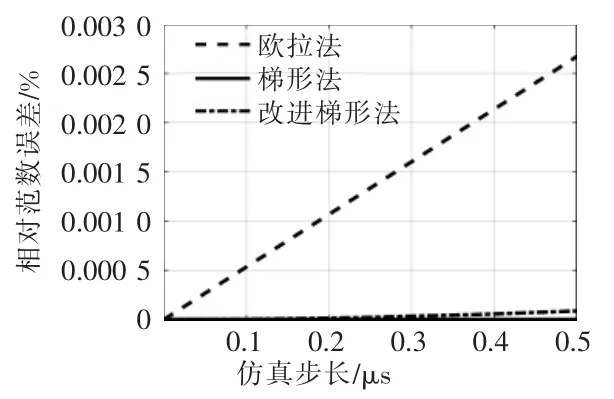
图4 buck 电路输出电压误差曲线Fig. 4 Error curves of buck circuit output voltage

表1 给出了本算例中不同算法预计计算时间，其中计算按1 个时钟周期（clk）计时（使用定点数计算），开关判断为1 clk，并行计算时间为最长路径计算时间。

仿真精度方面， 改进梯形法与梯形法相近，都远小于欧拉法；在计算时间方面，相较于梯形法，改进梯形法时间约减少了45.5%。

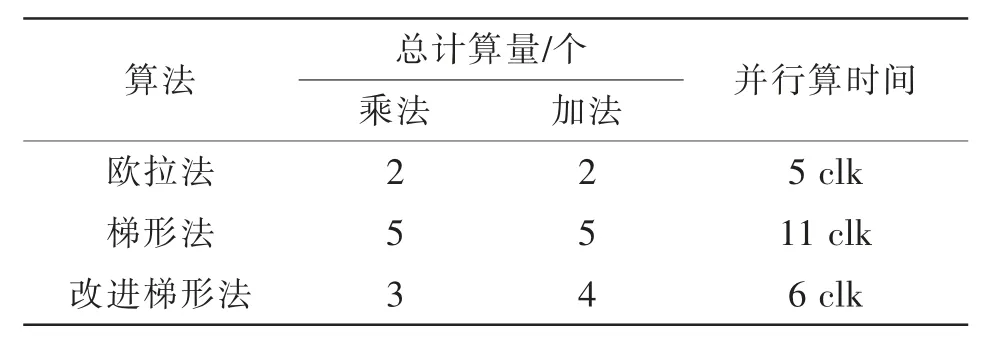
表1 不同算法预计计算时间Tab. 1 Computation time predicted using different algorithms

2.2 变步长算法计算步骤

文献[10]中的变步长算法，在完成插值后，将步长调整为原步长的一半， 使用欧拉法迭代计算2次，以此提高收敛性与计算精度，但在变步长时刻需要进行2～3 次迭代计算，仿真时间较长。 为加快计算速度，改进了变步长算法计算步骤[12]，计算流程如图5 所示。

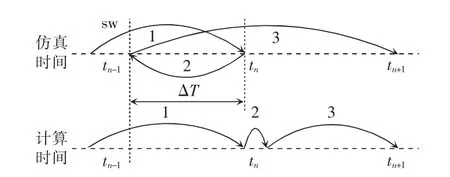
图5 改进的变步长算法计算流程Fig. 5 Calculation flow diagram of improved variablestep algorithm

步骤1从tn-1到tn时刻进行计算， 并检测到开关动作；

步骤2对状态变量插值，将状态还原到开关时刻tsw；

步骤3步长变为h+ΔT 进行仿真计算， 仿真时间与计算时间相等，保证实时性。

步骤2 和步骤3 对应的计算公式为

式中，ΔT 为图5 中对应的时间间隔。

在图5 计算过程中， 经过了2 次仿真计算，完成了2 个步长的仿真计算，可以保证每个步长只进行一次迭代计算，仿真计算时间稳定，单步长内计算快速。

2.3 改进的实时仿真数值计算方法

同时使用改进的梯形法、欧拉法、改进的变步长算法可以完成变步长计算，保证变步长计算中仿真结果的收敛性。 3 种方法都只进行一次矩阵乘法，计算速度相近，计算快速。

但由于FPGA 属于分布式处理器，每多一种情况都要预留相应的计算资源，同时使用3 种算法使FPGA 程序实现的难度提升， 因此需要对3 种算法（式（1）、式（3）、式（5））的计算结构进行改进，减少不同的计算分支。参考权重数值积分[9]的方法，将权重转变为几个确定的系数，通过控制系数进行计算[10]，将算法的选择转变为系数的选择，提升FPGA 程序效率。

以式（5）变步长算法的计算结构为原型，进行算法结构的改进；式（3）的改进梯形法与变步长算法结构相近，不做调整；式（1）欧拉迭代法向式（5）计算结构进行靠近，对式（1）进行扩充，增加2 个0系数的部分， 并将过程量等效为梯形法中的相等量，使计算结构靠近式（5），最终得到

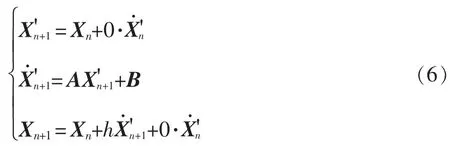
对式（6）、式（3）、式（5）相同部分进行提取，不同部分使用系数a、b、c 代替得到

系数a、b、c 的不同取值及其对应的算法如表2所示。 计算步骤如下。

步骤1通过开关动作采样程序， 得到上一个步长中的开关动作情况，即是否开关动作和动作时间点ΔT。

步骤2根据步骤1 中开关动作情况进行系数的选择，选择原则如下：

（1）判断开关是否动作。若开关未动作，使用改进梯形法；若开关动作，进入下一步判断。

（2）判断开关动作时间点ΔT。若ΔT>0，使用变步长算法；若ΔT=0，使用欧拉法。

步骤3根据选择的系数进行之后的计算。

除了只进行一次矩阵乘法计算快速外，与切换算法相比， 切换系数对FPGA 的资源占用减小很多，便于程序编写与仿真系统的建立；与使用多种算法相比，改进的算法计算结构在每个步长中的计算量一定，计算时间稳定，易于与通信程序和采样程序配合。

表2 不同算法对应系数设置Tab. 2 Coefficient settings of different algorithms

3 仿真算法FPGA 程序结构

3.1 实时仿真算法的FPGA 程序结构

FPGA 程序硬件设计结构如图6 所示，图中，实线部分为原有欧拉法定步长算法，虚线部分为本文算法增加部分，最下方为时间轴；图6 为一个步长中涉及的计算，计算模块是考虑并行运算的基础上根据计算的时间先后顺序进行排列，仿真计算时根据从左到右的顺序进行计算（对应时间轴相同即为并行运算）。

虚线部分改进主要体现在以下3 个方面：

（2）与系数a 相关的算法切换与数值补偿部分，可以与矩阵计算同时进行，不增加计算时间；

（3）与系数b 相关的控制步长变换部分。

与传统的定步长欧拉法计算对比，核心的矩阵计算时间不变，最长计算路径增加2 个乘法与1 个加法。仅需提取开关信号并对状态变量进行处理即可，不需要对算法进行根本的改动，便于对已有程序的结构进行升级与优化。

如图6 所示，在资源使用方面，增加计算资源主要针对状态变量的数量，正比于状态方程矩阵阶数；而整体计算资源近似正比于状态方程矩阵阶数二次方，即随着矩阵阶数增大，增加计算资源所占比例将逐渐减小。

图6 FPGA 程序硬件结构设计示意Fig. 6 Schematic of FPGA program hardware structure design

3.2 实时仿真算法的FPGA 程序结构

由于仿真所选拓扑不同、硬件不同，仿真时间不确定。 为保证对比简洁，以第2.1 节中的算例为例进行分析。 如图5 所示，变步长的插值算法需要增加1 个乘法与1 个加法。以算例中的并行计算方式统计预计计算时间，如表3 所示。

在本算例中，计算时间可以节省72%，由于本文算法所占据的时间可并行，不随矩阵阶数增加而增加，节省时间比率相对稳定。

表3 不同算法的计算时间Tab. 3 Computation time of different algorithms

4 实时仿真平台实验验证

4.1 仿真程序实验平台

本文使用的FPGA 开发板为Arria II GX 系列开发板，芯片型号为EP2AGX125EF35。 该FPGA 开发板提供124 100 个逻辑单元、576 个18×18 DSP乘法器，并配置频率100 MHz 晶振器，可以提供足量的计算资源。

实验数据通过Altera 公司的开发套件Quartus Prime 中SignalTap II 程序， 设置探针程序对FPGA仿真结果进行数据提取。

4.2 实验用仿真模型

仿真电路采用三相逆变器接LC 滤波器带对称阻感负载，电路拓扑如图7 所示，为方便程序计算规定点o 为参考节点。 电路模型使用状态变量法。开关模型方面， 开通等效为电压源串联电阻模型（见图7 中虚线），关断等效为开路。 仿真电路参数如表4 所示。

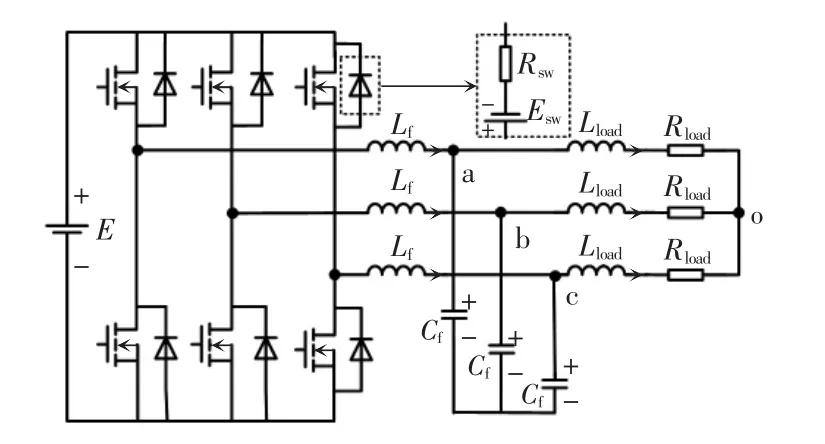
图7 三相逆变器电路拓扑Fig. 7 Topology of three-phase inverter circuit

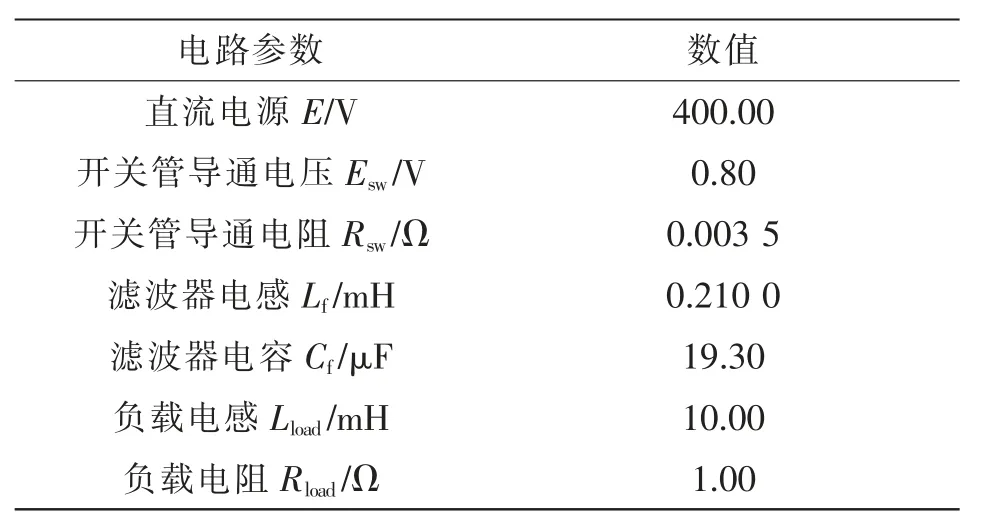
表4 仿真电路参数数据Tab. 4 Data of simulation circuit parameters

控制采用双极性正弦脉宽调制SPWM（sinusoidal pulse width modulation）控制，正弦波通过直接数字频率合成DDS（direct digital frequency synthesis）技术[15]将正弦波离散化后存入存储器中，根据仿真步长调用数据。 受开发板存储限制，为保证控制信号足够精确，排除控制不同带来的误差，输出设定为基频250 Hz 的三相正弦波，LC 滤波器的截止频率按照10 倍基频整定。

算例主要使用定点数的数值进行计算，本文算法计算使用时间为130 ns，步长设定在130 ns 以上即可保证实时性。 控制信号周期与步长同步，开关频率取110 kHz。

4.3 仿真结果对比与分析

4.3.1 算法收敛性验证

为便于观测发散现象，避免算法谐波误差与数值发散的结果叠加，步长采用本文算法500 ns 与欧拉法500 ns 进行仿真，仿真结果如图8 所示。 本文在计算时间方面与欧拉法相当，而在同样步长500 ns 情况下， 本文算法的输出波形是正常的正弦波形，而欧拉法出现了明显的数值发散情况。

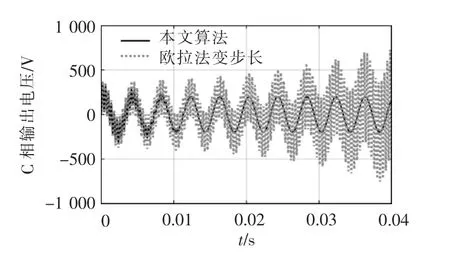
图8 不同迭代算法的仿真结果比较Fig. 8 Comparison of simulation results between different iterative algorithms

4.3.2 算法仿真验证

由于并行仿真无需预留过多通信时间，仿真步长可以接近计算时间， 算例中设置步长为150 ns，大于计算时间130 ns，满足实时性。 图9 为本文算法步长150 ns 下，三相逆变器的三相输出电压（图7 中为A 相uao、B 相ubo、C 相uco）与三相输出电流（图7 中为A 相iao、B 相ibo、C 相ico）。

由图9 可见， 逆变器输出电压和输出电流为平滑的三相正弦曲线，无谐波影响，本文算法的变步长部分计算正常，算法收敛性正常。仿真结果证明了算法的有效性。 将图9 中的计算结果与PLECS 软件变步长计算结果作对比，以A 相输出电压和输出电流为例，结果如图10 所示。使用式（4）对图9 的三相输出结果进行误差计算，计算结果如表5 所示。

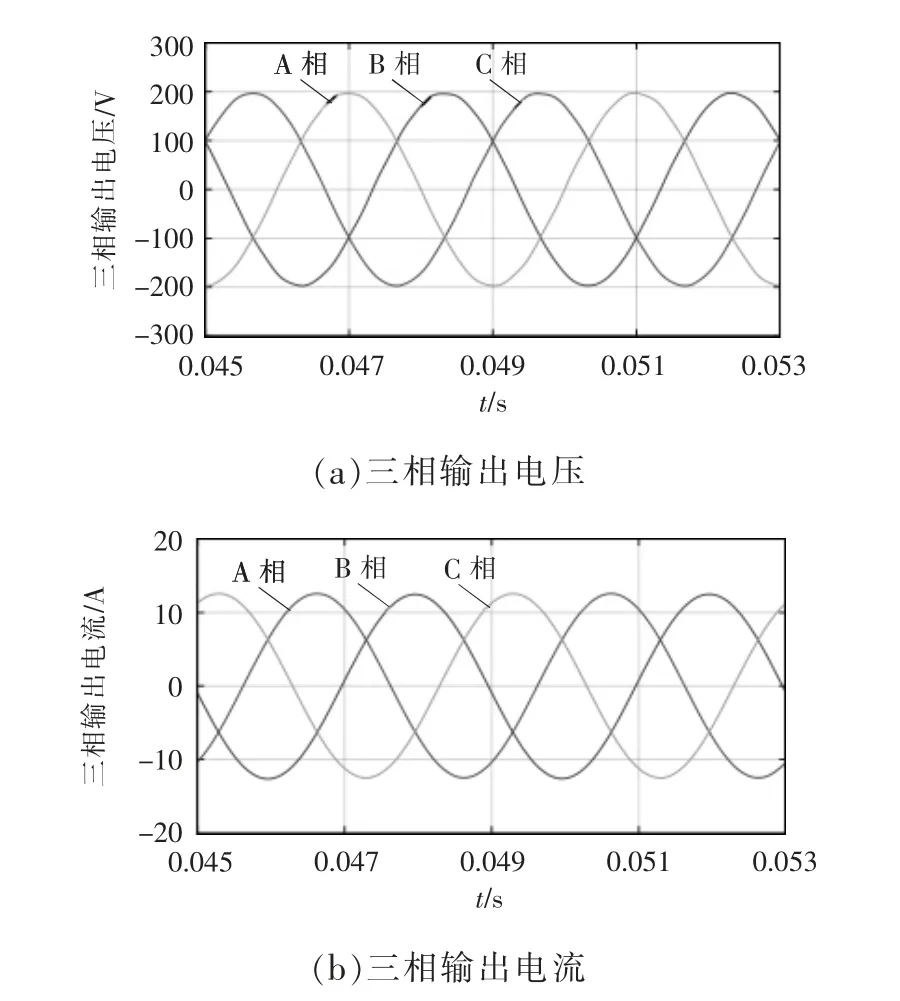
图9 三相逆变器输出波形Fig. 9 Output waveforms of three-phase inverter

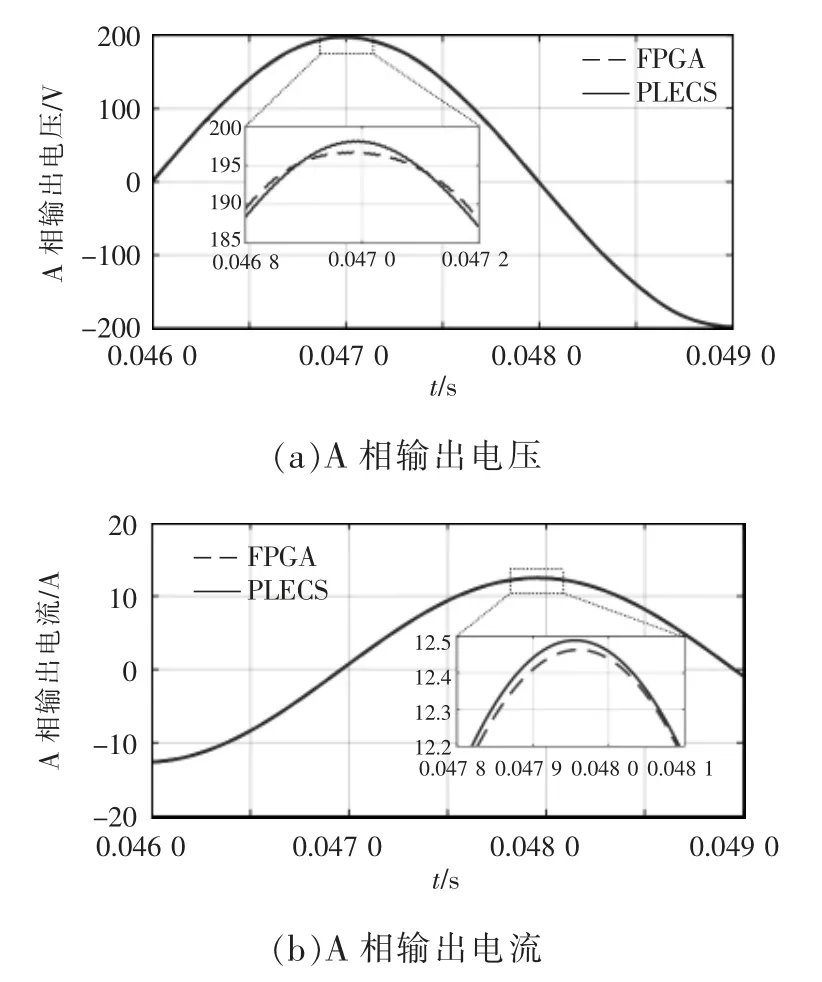
图10 A 相输出波形对比Fig. 10 Comparison of output waveform in phase A

表5 实时仿真结果误差Tab. 5 Errors of real-time simulation results

结果表示误差较小，仿真结果可用。 算法计算时间为130 ns，与一次欧拉法计算时间相近，而使用半步长欧拉法进行变步长计算，需要约3 倍的欧拉法计算时间。与之相比，本文算法可以节省约2/3的计算时间，而由于计算快速，步长较小，误差可以进一步减小。

5 结论

针对变步长实时仿真给嵌入式实时仿真带来的数值发散和计算时间不稳定的问题，提出一种基于FPGA 程序结构的实时仿真算法，优势为：①计算时间稳定；②收敛快且计算快速，相较于梯形法，计算时间减少近一半；③仿真精度方面，与梯形法相近，但远小于欧拉法。

稳定的计算时间有助于通信程序的设置与实时仿真模块之间的数据交互，而快速计算可以减小步长，有助于降低多重开关事件的出现，降低仿真计算难度。

算例中使用100 MHz 晶振的FPGA 开发板，如使用RT-LAB 等实验级FPGA 开发板，仿真速度还可进一步提升。后续将研究实验级FPGA 开发板对仿真速度的提升情况，进一步探究步长减小与电力电子仿真开关频率提升程度的具体关系。