半群H(n,m)的独立子半群
袁 月,赵 平
贵州师范大学 数学科学学院,贵阳 550025
设Sn和Tn分别是有限集Xn={1,2,…,n}上的对称群和全变换半群.对1≤m≤n-1,记Xm={1,2,…,m}且Xn-m=XnXm.令
T(n,m)={α∈Tn:Xmα=Xm}
G(n,m)={α∈T(n,m):Xn-mα=Xn-m}=T(n,m)∩Sn
H(n,m)={α∈T(n,m):Xn-mα⊆Xn-m}
则易证得G(n,m),H(n,m)和T(n,m)都是全变换半群Tn的子半群,且G(n,m)⊆H(n,m)⊆T(n,m).

设S是半群H(n,m)的子集.通常,用E(S)表示S中的所有幂等元组成的集合.本文未定义的术语及符号请参见文献[16].
为了叙述上的方便,在H(n,m)上引入以下的二元关系:对任意α,β∈H(n,m),定义
αL◇β⟺im(α)=im(β)αR◇β⟺ker(α)=ker(β)
αJ◇β⟺|im(α)|=|im(β)|αH◇β⟺im(α)=im(β),ker(α)=ker(β)
则L◇,R◇,J◇与H◇都是H(n,m)上的等价关系.
易得L◇⊆J◇,R◇⊆J◇且H◇=R◇∩L◇.对r∈N+且2≤m+1≤r≤n,记

约定:设1≤m≤n-1,令Sn-m,Tn-m分别表示Xn-m上的对称群和全变换半群,Sm表示Xm上的对称群.

证 由文献[15]可知
G(n,m)=〈(12),(12…n),((m+1)(m+2)),((m+1)(m+2)…n)〉≅Sm×Sn-m

当2≤m≤n-3时,任意取α∈H(n,m),定义βα,λα∈Tn为
显然βα,λα∈H(n,m)且βα∈G(n,m).任意取i∈Xn,若1≤i≤m,则iβα=iα∈Xm,于是(iα)α≤m,从而i(βαλα)=(iβα)λα=(iα)λα=iα;若m+1≤i≤n,则由α∈H(n,m)可得iβα=i∈Xn-m且iα>m,从而i(βαλα)=(iβα)λα=iλα=iα.因此α=βαλα.易知
βα∈〈(12),(12…m)〉≅Sm

Akα=ak1≤k≤r
且xα=xx∈Xn(A1∪…∪Ar)

证设
其中Xm={a1,a2,…,am}且{am+1,am+2,…,an}⊂Xn-m.令
则μα∈G(n,m),且
于是α*=αμα∈〈G(n,m),α〉,且
从而
再由引理1可得H(n,m)=〈G(n,m),α〉.

证令k=min{|im(ε)|:ε∈E(T)∩H(n,m)(n-2)},则m+1≤k≤n-2.假设m+2≤k≤n-2.任意取
其中Xn-m=Am+1∪Am+2∪…∪Ak,且ai∈Ai(m+1≤i≤k).由|im(ε)|=k≤n-2可知,存在t∈{m+1,m+2,…,k},使得|At|≥3,或者存在p,q∈{m+1,m+2,…,k}且p≠q,使得|Ap|=|Aq|=2.以下分两种情形:
情形1 |At|≥3.取b,c∈At{at}且b≠c.令
则α2=β2=ε,从而α,β∈T.由|im(ε)|=k≥m+2可知,存在i∈{m+1,m+2,…,k},使得Ai∩At=Ø.不失一般性,不妨设i>t.令
则(α*)2=αβ∈T且(β*)2=βα∈T,从而α*,β*∈T.易验证
显然α*β*α∈E(T)∩H(n,m)(n-2),且|im(α*β*α)|=k-1,与k的极小性矛盾.
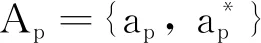
则α2=β2=ε,从而α,β∈T,因此αβ,βα∈T.令
则(α*)2=(γ*)3=βα∈T,(β*)2=αβ∈T,从而α*,β*,γ*∈T.易验证
显然(α*β*γ*)2∈E(T)∩H(n,m)(n-2),且|im((α*β*γ*)2)|=k-1,与k的极小性矛盾.


证任意取
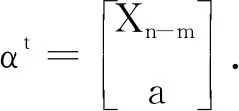
其中b∈Xn-m.若a=b,则αt=ε∈T,从而α∈T;若a≠b,令
其中a,b,c∈Xn-m且a,b,c互不相同,则β2=γ2=ε,从而β,γ∈T.令
则

对r∈N+且2≤m+1≤r≤n,记
Sing(n,m)={α∈H(n,m):|im(α)|≤n-1}
则H(n,m)(r)是H(n,m)的理想,且Sing(n,m)=H(n,m)(n-1).




易验证αsβs=γs-1.注意到













引理9设1≤m≤n-3,T是半群H(n,m)的独立子半群,若T∩G(n,m)≠Ø,则G(n,m)⊆T.
证由T∩G(n,m)≠Ø可知,存在α∈T∩G(n,m),于是1Xn=αn!∈T,其中1Xn是Xn上的恒等变换.任取β∈G(n,m),则βn!=1Xn∈T,从而β∈T.由β的任意性可得G(n,m)⊆T.

定理1设1≤m≤n-3,则半群H(n,m)的独立子半群有且仅有以下5类:


证注意到G(n,m),Sing(n,m)都是半群H(n,m)的子半群,G(n,m)∩Sing(n,m)=Ø且H(n,m)=G(n,m)∪Sing(n,m),则由文献[14]可知,G(n,m),Sing(n,m)和H(n,m)都是半群H(n,m)的独立子半群.由引理7、引理8可知,类型,都是半群H(n,m)的独立子半群.
情形1E(T)∩G(n,m)≠Ø且E(T)∩Sing(n,m)=Ø.由引理9可得G(n,m)⊆T.我们断言T∩Sing(n,m)=Ø.假设α∈T∩Sing(n,m),则存在n∈N+,使得αn∈E(T)∩Sing(n,m),与E(T)∩Sing(n,m)=Ø矛盾.因此T=G(n,m).

情形2.1E(T)∩H(n,m)(n-2)≠Ø.由引理3、引理4、引理5可得Sing(n,m)⊆T,从而T=H(n,m).


情形3.1E(T)∩H(n,m)(n-2)≠Ø.由引理3、引理4、引理5可得Sing(n,m)⊆T,从而T=Sing(n,m).

ΓT={x∈Xn-m:存在k∈Xn-m,使得λ(x,k)∈E(T)}
假设|ΓT|≥3,则存在t1,t2,t3,k1,k2,k3∈Xn-m,ti≠ki(1≤i≤3)且t1,t2,t3互不相同,使得λ(t1,k1),λ(t2,k2),λ(t3,k3)∈E(T).显然存在i∈{2,3},使得t1≠ki.若ti=k1,则k1≠ki,从而
这与E(T)∩H(n,m)(n-2)=Ø矛盾.若ti≠k1且ki=k1,则
这与E(T)∩H(n,m)(n-2)=Ø矛盾.若ti≠k1且ki≠k1,则


注1易知半群H(n,n-1)唯一的独立子半群是它本身,H(n,n-2)的所有独立子半群为半群H(n,n-2),G(n,n-2),Sing(n,n-2),{λ(m+1,m+2)}和{λ(m+2,m+1)}.

