浅谈几何解题思维在数学教学过程中的应用与实施
王春华


[摘 要:在几何的教学过程中,在讲清楚基本概念的同时,要有意识地培养学生利用学过的知识,通过类比、联想、拓展等数学方法,从多个方面去思考和解决问题,一题多解。教师在课堂上,要多挖掘一些行之有效的一题多解的例题和习题,去锻炼培养学生的思维应变能力
关键词:一题多解;数学思想;探索创新]
八年级阶段,学生开始全面接触平面几何问题,对几何问题的解决方法有了一定的认识和了解。但学生的几何思维还稍显稚嫩,对定理的把握,對方法的总结,对技巧的应用,均还在初级的形成阶段。这个时候,如果学生的思维能够打开,逐渐形成多角度,全方位去思考问题的习惯,对于后面几何问题的学习,就大有裨益。因此,在几何的教学过程中,在讲清楚基本概念的同时,要有意识地培养学生利用学过的知识,通过类比、联想、拓展等数学方法,从多个方面去思考和解决问题,一题多解,并注意总结解题特征,解题方法,最后达到触类旁通,融会贯通,从而开拓自己的几何思维,形成全面、严谨、灵活地解决几何问题的习惯。
我们教师在课堂上,要多挖掘一些行之有效的一题多解的例题和习题,去锻炼培养学生的思维应变能力。下面,我就以我们平时课堂上和教材上出现的一些简单而又经典的问题进行详细讲解。
以人教版八年级数学第十八章《平行四边形》第18.1.2节《三角形的中位线》为例,在这一节中,教材给出了三角形的中位线的概念,中位线定理的内容及其证明。
教材原文如下:
此题的解题方法,对于同学们来讲,并不是很陌生。特别是辅助线的做法,我们在全等三角形的证明中提及过,当遇到中点时,我们可以通过倍长过中点的线段来构造全等三角形。这里通过倍长,构造了一组对角线互相平分,从而构造出平行四边形,再通过平行四边形的性质进行下一步证明。此题的辅助线较多,而且学生刚接触平行四边形不久就让其构造平行四边形,难度相对较大,绝大多数同学还停留在全等三角形的相关知识。但是,学生在看到中点后,应该要有构造等长线段的这种意识。而这种意识的形成,就需要我们老师在课堂上,通过类似的例题进行训练,发散学生的思维。下面,我们通过改变中位线定理的题设和结论,得到一个新的命题,并证明该命题为真命题。
母题1:
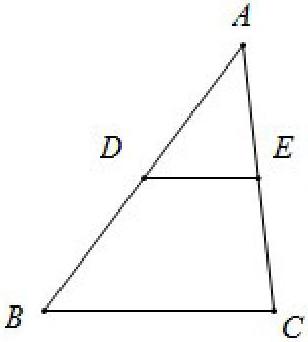
如图所示,在△ABC中,D为边AB的中点,
过点D作DE∥BC,交边AC于点E。
求证:E为AC的中点。
此题,对于很多学生来讲,觉得是显而易见的结论,但要进行严格的证明,我相信,有相当一部分学生是有困难的,这一点,也在我的课堂上得到了验证。但同时,对于一些思维发散的学生来讲,证明的方法又显得多种多样,下面我们就来探讨下该题的多种解题方法。
解法一:利用平行线分线段成比例定理或者三角形相似的性质来做,相对较简单,但是这是九年级的知识,八年级的绝大多数学生并不清楚,对于他们来讲并不适用,此处不再详细介绍。
解法四:构造全等三角形证明线段相等。这种方法应该是学生们最熟悉也经常用的方法。有中点,则有线段相等,只需要构造出另外的边相等或者角相等即可实现两三角形全等。
解法五:利用等面积法证明线段相等。等面积法在初中阶段,是一种非常重要的证明线段相等的办法,有时候会起到柳暗花明的效果,在平时的要跟学生渗透这种思想方法。
解法六:取AC的中点,再证该点和E点是同一点即可。此法思维的难度较大,学生可能一时难以理解和掌握,但此法在高中的平面几何和立体几何中非常常见,是比较常规的证明点在线上,或者某点是何特殊点的方法,在初中阶段,对于有能力的学生,可以适当渗透。
即E为AC的中点。
通过上述的例题我们可以看到,一道非常简单的几何题中,蕴含了了非常多的数学思想和方法。如果我们在教学过程中,能从多个角度去剖析这道题的话,不仅能让学生很好地巩固和升华已学的知识点和数学思想方法,更重要地是能让学生理清楚这些方法中的内在联系,进一步发散自己的几何思维。同时,从这些多样化的方法中,学生容易找到满足感和成就感,从而提升自己学习数学的信心,促进学习数学的兴趣,一举多得。
其实,教材在编排的时候,非常注意这些思想方法的渗透,我们老师对这些经典例题和习题千万不要浅尝辄止,也应该像教材一样润物细无声,逐步完成对学生的思想和方法的渗透
我们再来看一下本章习题18.2拓广探索的第16题。
教材母题2:
如图,在△ABC中,BD,CE分别是边AC,AB上的中线,BD与CE相交于点O. BO与OD的长度有什么关系?BC边上的中线是否一定过点O?为什么?(提示:分别作BO,CO的中点M,N,连接ED,EM,MN,ND.)
分析:本题通过构造中位线,得到四边形EMND为平行四边形,利用其对角线互相平分得出第一问的结果:BO=2 OD.而第二问,对于八年级的学生来说,是有一定的难度的,考察的是如何证三线共点的问题。教材其实在前面也以练习的形式,让学生们证明了三角形的三条角平分线,三条垂直平分线交于一点,这两条线交于一点的证明难度较小,直接利用角平分线和线段垂直平分线的性质就能解决。而要解决此题,必须要跟学生渗透证明三线共点的两种最基本的思想方法:1、连接并延长AO,与BC交于点F,说明AF是△ABC的中线;2、取BC的中点F,连接AF,证明AF经过点O。
下面我们从这两个方面采取不同的方法去解决这道题:(第一问的证明比较简单,直接应用中位线定理即可,证明过程略过)
以上几例,蕴含的数学思想方法有些并不简单,但是我们可以通过不同的切入点,和我们学生已经学过的知识结合起来,通过最基本的方法证明出结论。在这种一题多解中渗透思想方法,让学生的兴趣大增,学生在解题过程中愿意思考,敢于探索,提升了数学素养,培养了多元思维和创新能力。当然,上述枚举的几例,是站在老师角度去思考的,对于八年级的学生来讲,可能有些还会存在些许难度,特别母题2的面积法,对思维程度稍微差一点的学生来讲,会有些混乱,此时,我们老师在课堂上,不能为了只为了单纯追求多解泛泛而讲,我们应该立足在一题多解的基础上,追寻解决该问题的本质,找到知识点之间的联系,从而使学生的知识多样化和系统化,只有这样,他们才会在解题的过程中真正达到一题多解,对数学知识达到升华。
参考文献
[1]人教版八年级数学教师教学用书.
[2]王海军.一题多解和一题多变在初中数学教学中的应用[J].考试周刊,2017(68).
[3]姚大鹏.一题多解 夯实基础 培养能力[J].科教导刊(中旬刊).2016(08).
[3]农秀丽.论高考数学试题解法的一题多解[D].百色学院学报.2011:88-94.
广州市黄埔广附实验学校 510000

