非线性奇摄动积分-微分发展方程Robin问题广义解

冯依虎 莫嘉琪

(1-亳州学院电子与信息工程系，亳州 2 36800; 2-上海大学数学系，上海 2 00436;3-安徽师范大学数学与统计学院，芜湖 2 41003)

1 引言

非线性积分-微分方程模型在数学物理、工程数学、生态数学、物理化学等应用数学学科中都有很广泛的应用.利用奇异摄动方法来求解相应的数学模型，诸多学者已经做了很多研究[1-9].Mo等[10-17]用多重尺度、同伦映射、变分迭代等理论，讨论了一类反应扩散、大气物理、光晶格等方面的问题.Feng等[18-26]也用奇异摄动方法对一类孤立子波、分数阶微分方程、自治系统等模型也做了一些工作.

本文是利用奇摄动理论和方法来讨论一类发展方程Robin问题，得到了相应模型的一致有效的广义渐近解.

现讨论如下奇摄动积分-微分发展方程Robin问题

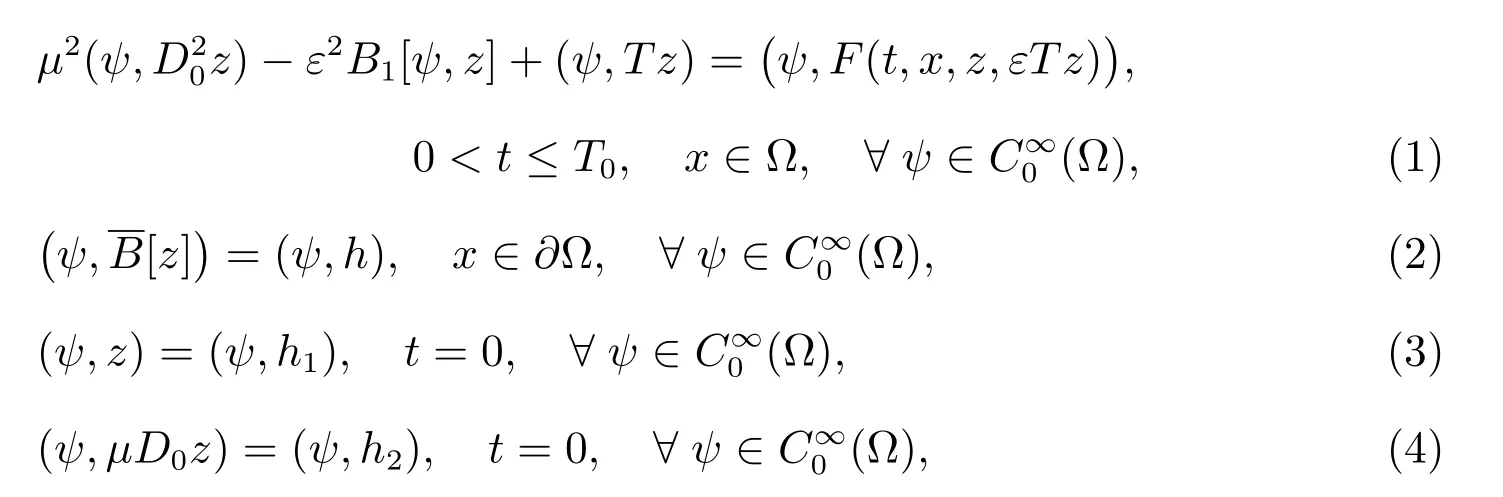
微分算子

系数αµσ是在C∞(Ω)中的实值函数，L为一致椭圆型算子，T为积分算子

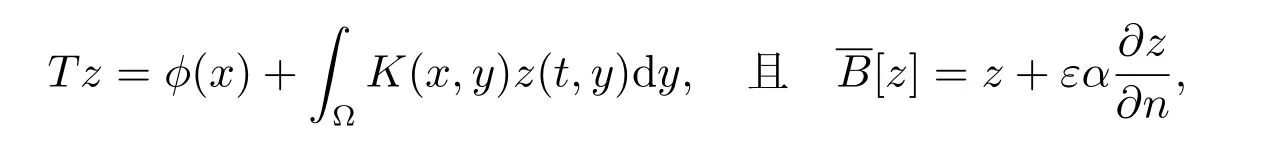
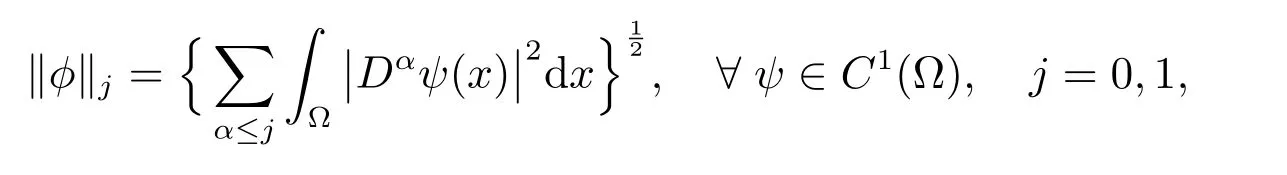
(v,z)是被定义在H1(Ω)上的内积.

我们假设：

(H1): 微分-积分发展方程(1)–(3)的退化情形的积分方程

有解U00∈H1(Ω)；

(H2): 下列方程

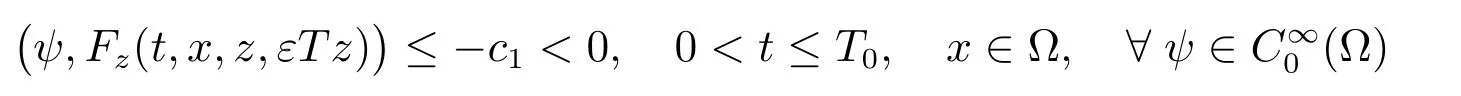
成立，其中c1为正的常数.

2 Fredholm积分方程广义解

现构造发展方程模型(1)–(4)的广义外部解U.设

将(6)式代入积分-微分发展方程(1)，按ε和µ的幂展开对应的非线性项F，合并εrµs同次幂的系数.取对应ε0µ0的系数为零，它就是Fredholm积分方程(5).由假设知，它的解为U00.

取对应εrµs(r,s=0,1,···,r+s̸=0)幂的系数为零，可得如下Fredholm积分方程

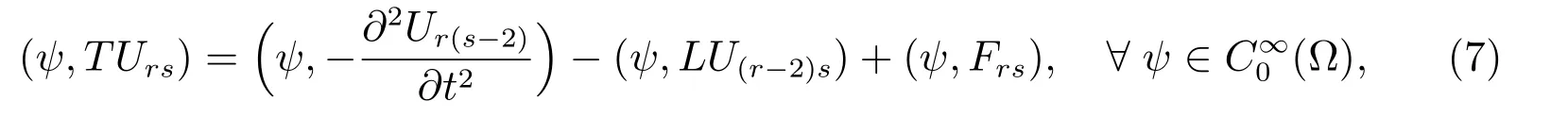
其中

由Fredholm积分方程(7)，可以得到对应的广义解Urs(r,s=0,1,···,r+s̸=0).将它们代入(6)式，便得到积分-微分发展方程模型(1)–(4)的广义外部解U.但它未必满足模型的边界条件(2)和初始条件(3),(4).因此，我们还需构造积分-微分发展方程模型(1)–(4)广义解的边界层校正项V和初始层校正项W.

3 解的边界层校正

在区域Ω边界∂Ω的邻域上建立一个局部坐标系(ρ,φ)：设在边界∂Ω的邻域中的点P∈Ω的坐标ρ(ρ≤ρ0)是点P到∂Ω的距离，这里ρ0>0为足够小的常数，使得在∂Ω上的每一点的内法线在∂Ω的邻域0≤ρ≤ρ0中互不相交.坐标φ=(φ1,φ2,···,φn−1)是在n−1维边界∂Ω上的一个非奇异坐标系，并设∂Ω的邻域中点P的坐标φ是通过点P的内法线与边界∂Ω的交点Q的坐标φ相同.因此，在∂Ω的邻域0≤ρ≤ρ0中

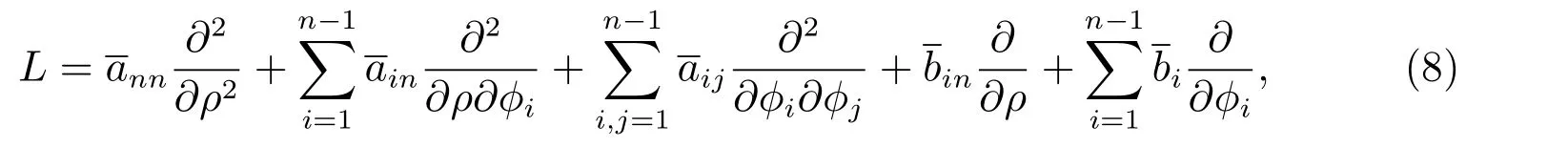
其中

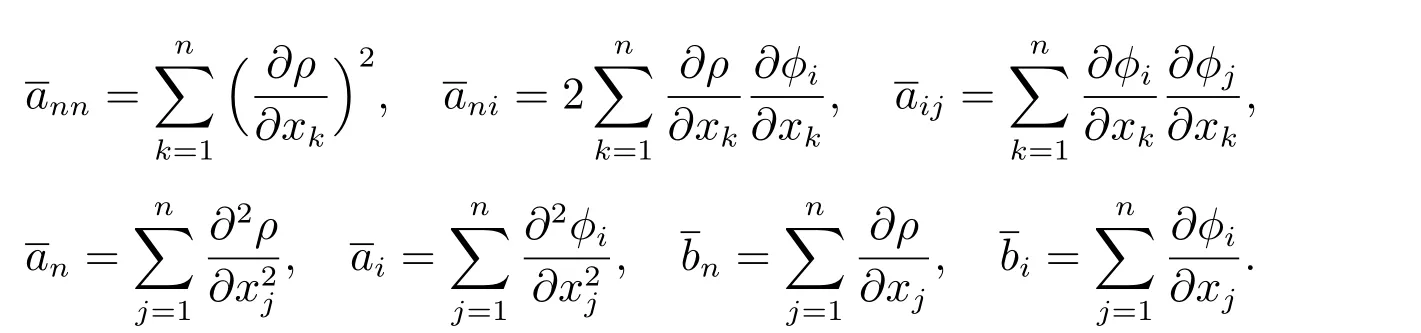
现作多重尺度变量[1,2]

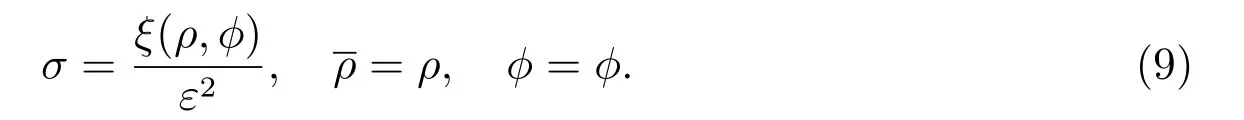
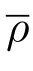
而

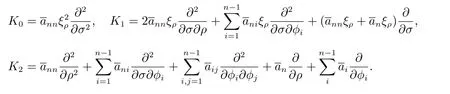
设模型(1)–(4)的边界层校正项为V，模型的广义解z为

将(11)式代入关系式(1),(2)，可得

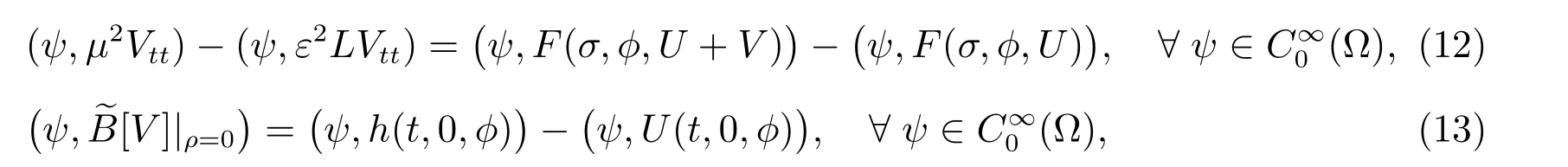
其中边界算子～B[·]为

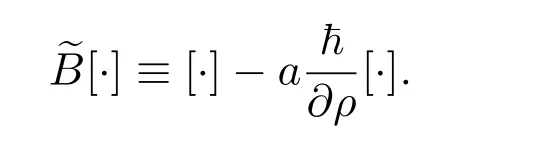
再设

将(11),(14)式代入式(12),(13)，并按ε及µ的幂展开，合并εrµs的同次幂项，有

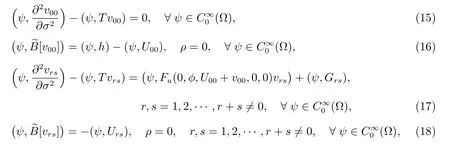
其中Grs(r,s=1,2,···,r+s̸=0)为逐次已知的函数，其表示式从略.

由广义积分-微分发展方程问题(15)–(18)，依次可得vrs(r,s=1,2,···).再由假设知vrs具有如下广义边界层型的性态

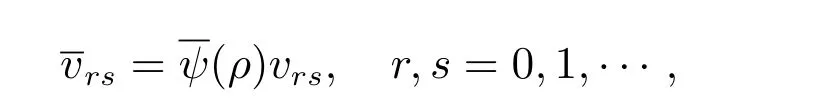
4 模型广义解的初始层校正

设广义积分-微分发展方程模型(1)–(4)的初始层校正项为W，而模型的广义解z为

且设

将(20),(21)式代入关系式(1),(3)和(4)，按ε,µ的幂展开非线性项，合并εrµs同次幂的系数，有

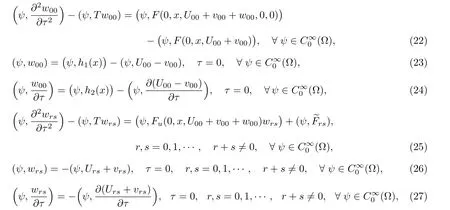
再由假设知，vrs具有如下广义初始层型的性态

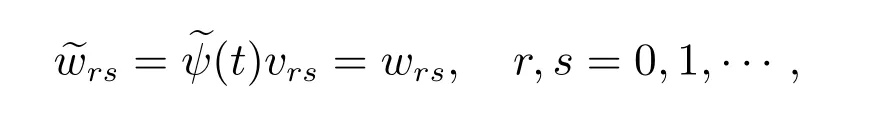
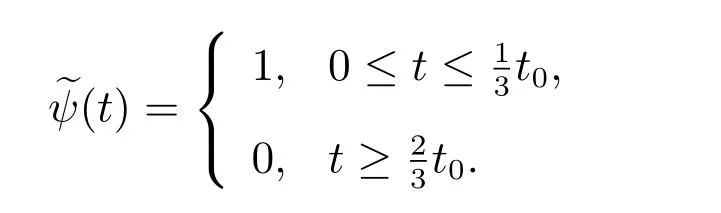
因此，我们构造两参数非线性广义积分-微分发展方程模型(1)–(4)的广义解z有如下形式渐近展开式

5 广义解的一致有效性

现在用泛函分析不动点理论来估计积分-微分发展方程模型(1)–(4)广义渐近展开式(29)的余项R.设

其中

利用(30)式和边界层，初始层校正项的性态(19)和(28)式，有

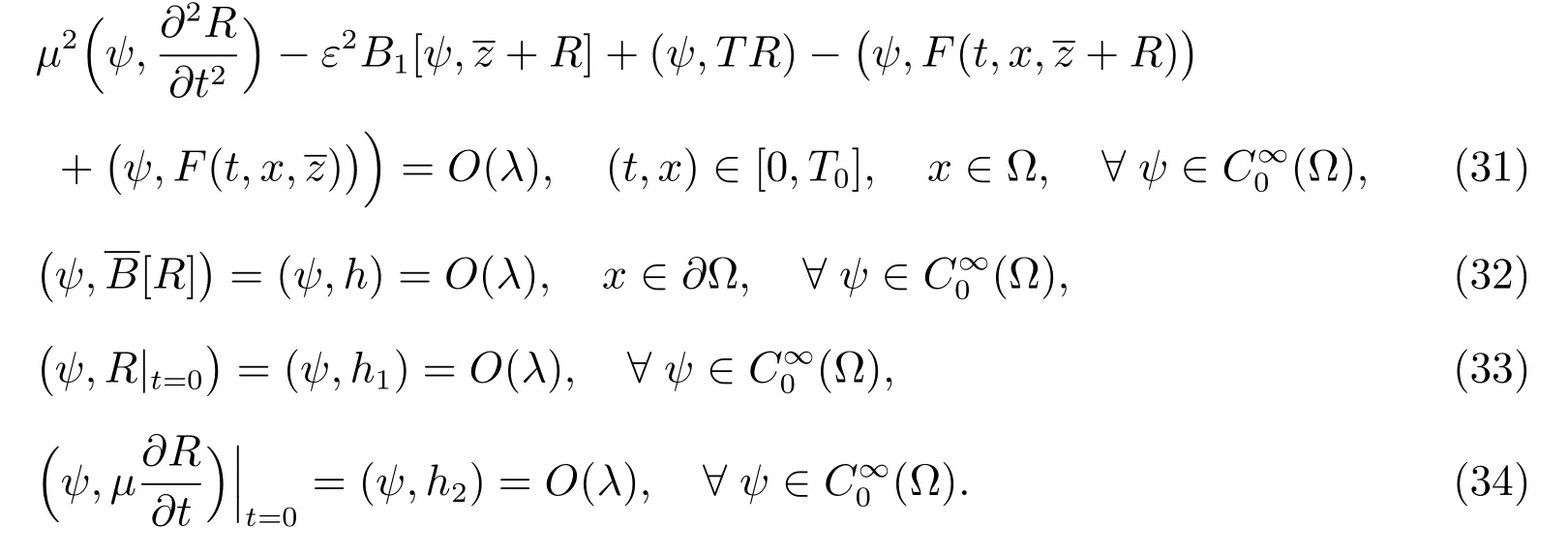
由(31)–(35)式，有

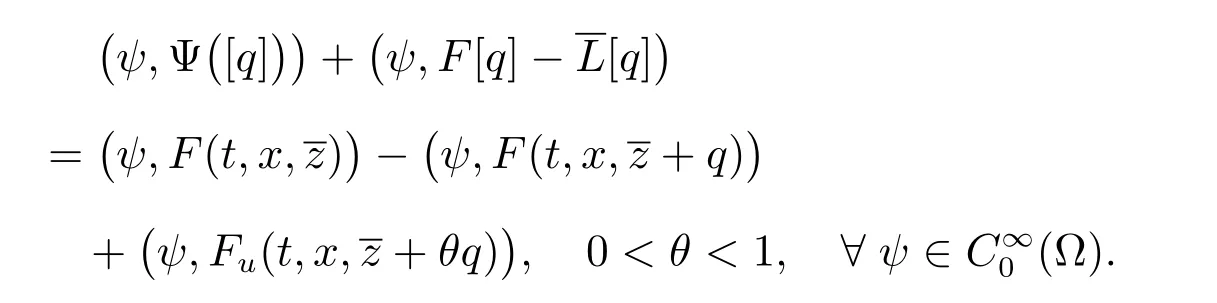
固定ε,µ，取线性赋范空间N:N={q|q∈C2((0,T]×Ω)}，得

且有范数

设Banach空间B和范数分别为

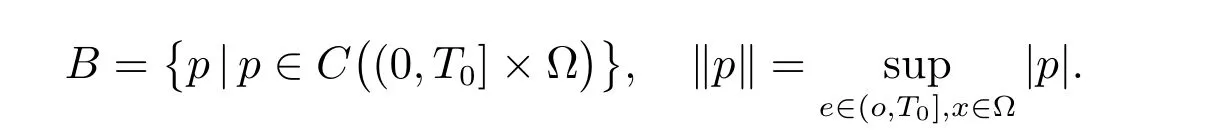
由假设

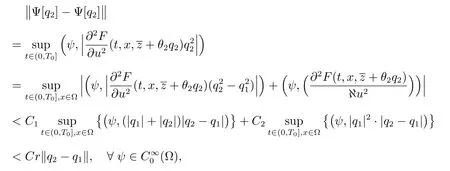
其中C1,C2和C均为独立于ε,µ的常数，且对任意的q1,q2在球KN(r),‖r‖≤1中成立.再由泛函分析不动点定理[1,2]，奇摄动非线性积分-微分发展方程模型(1)–(4)广义解的渐近展开式(29)的余项R满足

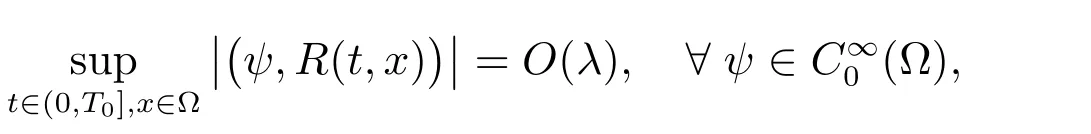
这里

λ=max(εM+1µM,εMµM+1),0<ε,µ≪1.

因此，得到如下定理：

6 结论与应用前景

广义非线性奇异摄动积分-微分发展方程模型的奇摄动求渐近解的方法在应用数学，工程数学等各学科中有广泛的应用.本文是利用幂级数展开技术，伸长变量和多重尺度变换技巧，合成展开理论来求解相应的数学模型，构造了广义解的近似展开式并用不动点理论证明了广义解的渐近展开式的一致有效性.

用奇异摄动方法得到的解是渐近解析式，它不同于用一般的数值计算方法得到的解.因为得到的渐近解析式还可继续进行微分，积分等解析运算，从而来进一步得到解的更多性态及相关的物理量的定性、定量的描述.然而，用一般的数值计算方法所得到的模拟解是不能达到的.因此，从这一观点来说，在本文中对广义非线性奇异摄动积分-微分发展方程模型用奇摄动方法得到解的渐近解析式具有良好的应用前景.