压缩感知中l1问题的自适应罚参数交替方向法
徐 丽 君,胡 瑞 戈,李 婷
(大连海事大学 理学院, 辽宁 大连 116026 )
0 引 言
Candes等[1]以及Donoho[2]提出的压缩感知作为一个新的采样理论,通过开发信号的稀疏特性,在远小于奈奎斯特采样率的条件下,用随机采样获取信号的离散样本,通过重建算法完美地重建信号.压缩感知理论一经提出,就引起学术界和工业界的广泛关注.它在信息论、图像处理、地球科学、光学微波成像、模式识别、无线通信、生物医学工程等领域受到高度关注.
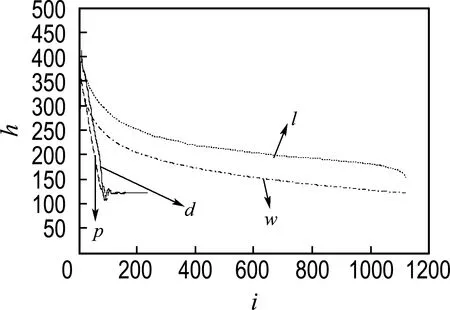
假设x0∈Rn是希望得到的原始稀疏信号,不直接对x0进行采样,而是先得到一组线性观测数据b=Ax0∈Rm,其中A∈Rm×n是编码矩阵,m 这是一个NP难的组合优化问题.因此,更好更可行的方案是求解凸优化l1问题(基追踪问题): 因为上述两个问题在某些有利条件下具有相同的解[3]. 当b包含噪声或当x0不完全稀疏而只是可压缩时,对基追踪问题进行一定的松弛,使得基追踪问题转化为约束基追踪去噪问题: 或非约束基追踪去噪问题: 其中δ>0,μ>0是参数.从优化理论角度出发,约束基追踪去噪问题和非约束基追踪去噪问题是等价的.而本文只对非约束基追踪去噪问题进行研究. 过去学者们构造了一些迭代算法来求解上述稀疏优化问题,如牛顿内点法[4]、高效近块坐标同伦算法[5]、贪婪算法[6-7]、基于迭代收缩软阈值理论的固定点连续算法(FPC)[8]、梯度投影算法[9-10]、快速迭代收缩软阈值算法(FISTA)[11]、稀疏重构算法(SpaRSA)[12]、基于梯度理论的分块坐标梯度下降法(CGD)[13]、光谱投影梯度法(SPGL1)[14]、Bregman迭代算法[15]等.Yang等[16]将交替方向法(alternative direction method,ADM)引到压缩感知领域中解决l1问题,但在求解过程中,并没有对增广拉格朗日函数中的罚参数进行深入研究.尽管理论上只要罚参数大于零就可保证ADM的全局收敛性,但在实际计算过程中罚参数的取值也会大大影响收敛速度. 针对上述问题,本文考虑根据迭代过程中某些量的数值关系,探讨罚参数的动态调整准则,设计一种自适应的罚参数调整方法,以便能够快速且稳定地获得最优解. 设函数f(x):Rm→R和g(y):Rn→R都是凸函数且相互独立,x∈Rm,y∈Rn是优化变量,等式约束中A∈Rp×m,B∈Rp×n,b∈Rp,凸优化问题为 上述问题的增广拉格朗日函数为 L(x,y,λ)=f(x)+g(y)-λT(Ax+By-b)+ 其中λ是拉格朗日乘子,β>0是罚参数.为了获得最优解,通过增广拉格朗日函数进行迭代,其中第k步迭代如下: 对于上述迭代,需要同时计算x和y,这是比较困难的.而ADM把复杂的联合最小化问题转变为两个简单子问题:第1步,已知(yk,λk)极小化函数L(x,y,λ),求得xk+1;第2步,已知(xk+1,λk)极小化函数L(x,y,λ),求得yk+1;第3步,已知(xk+1,yk+1)更新拉格朗日乘子λ.具体迭代如下: 基于ADM的思想和框架,引入辅助变量r,使非约束基追踪去噪问题转化为变量可分离问题: 于是,上式的增广拉格朗日函数为 (1) 其中y∈Rm是拉格朗日乘子.对问题(1)使用交替极小化,具体步骤如下: 步骤1给定x=xk和y=yk,求问题(1)关于r的最小值rk+1为 rk+1=(μβ/(1+μβ))(yk/β-(Axk-b)) (2) 步骤2给定y=yk和r=rk+1,求问题(1)关于x的极小化问题,易知该问题可等价为下面的问题: 通过下面近似求解来替代对该问题精确求解: 其中τ>0是邻近参数,且 gkAT(Axk+rk+1-b-yk/β) 最后得出解 xk+1=Shrink(xk-τgk,τ/β)= max{|xk-τgk|-τ/β,0}∘ ((xk-τgk)/|xk-τgk|) (3) 其中式(3)用的是软阈值算法,“∘”代表分量乘法. 步骤3给定x=xk+1和r=rk+1,更新乘子y: yk+1=yk-γβ(Axk+1+rk+1-b) (4) 其中γ>0是步长常数. 由以上推导,对非约束基追踪去噪问题应用ADM产生的迭代过程如下: rk+1=(μβ/(1+μβ))(yk/β-(Axk-b)) xk+1=Shrink(xk-τgk,τ/β) yk+1=yk-γβ(Axk+1+rk+1-b) (5) 上述迭代过程实际上是一个不精确的ADM,因为在求解xk+1时用近似求解来代替精确求解.文献[17]中只研究了γ=1时的收敛性,而文献[16]对于γ>1的情况也给出了收敛结果并做出了证明. 考虑非约束基追踪去噪问题的对偶问题: 写出增广拉格朗日子问题: 其中x∈Rn是一个乘子(实际上是原变量).这里假设矩阵A满足AAT=I,对对偶问题用ADM,迭代如下: (6) 值得注意的是,当且仅当r=μy时非约束基追踪去噪问题的对偶问题中等式成立.因此,原始-对偶残差和对偶间隙如下: 在计算中,迭代式(6)被下式终止: 其中ε>0. 本文主要针对对偶问题的ADM进行改进,即迭代式(6).文献[16]中已经给出:对偶问题的ADM比原始问题的ADM更有效. 罚参数β是ADM中的一个重要参数,虽然理论上只要β>0就可保证ADM的全局收敛性,但实际计算中β过大或过小都会影响收敛速度.以本文研究的对偶问题的ADM为例,即迭代式(6),目前在罚参数β的选取上是固定的,即在迭代过程中不改变罚参数的取值,除非过大或过小.然而,在许多问题中,固定的β在迭代过程中,并非都是有效的.换言之,对目标函数的寻优和约束条件的惩罚不起作用.此时,依然使用该罚参数就会影响效率. 针对上述问题,本章首先分析罚参数在迭代过程中对目标和约束的影响,然后根据其相对变化量,提出一种动态调整罚参数的策略,使得ADM在迭代过程中自动选取合适的β,使本文方法更有效. 首先,将增广拉格朗日子问题中给定的常值β改写为与迭代步k相关的βk: 由于βk在目标函数中相当于对惩罚项(即对偶问题约束条件)的一种权重,其大小直接影响对偶问题目标函数下降和约束条件的满足情况.因此基于迭代过程中对偶问题目标函数值的相对变化量与约束函数值的相对变化量,判断βk是否应该调整以及该如何调整. (1)对偶问题目标函数值的平均相对变化量: (2)对偶问题约束函数值的平均相对变化量: 其中xk、rk表示经过k次迭代后的值,xk+j、rk+j表示经过k+j次迭代后的值.为了比较这两个值的大小,采用计算两个平均相对变化量之比 Δ=Δ1/Δ2 来进行量化. 若βk取值恰当,Δ1和Δ2的值是相近的,从而Δ会在阈值内(Δ∈[δ1,δ2]),其中δ1<δ2是事先取定的值.若Δ不在此区间范围,则说明当前的罚参数βk在一定程度上不合适,需要进一步分析调整. 显然,当βk过大时,Δ1<Δ2,即对偶问题目标函数值下降速率相对较慢,通常会出现Δ<δ1;当βk过小时,Δ1>Δ2,即对偶问题约束函数值下降速率相对较慢,通常会出现Δ>δ2. 根据上述分析,给出自适应罚参数调整准则: 当Δ∈[δ1,δ2]时,βk+1=βk; 当Δ<δ1时,调小罚参数:βk+1=aβk; 当Δ>δ2时,调大罚参数:βk+1=cβk. 其中a<1,c>1是常数,称其为调节参数. 将上述罚参数调整准则应用到原始的ADM,给出本文的自适应罚参数ADM: (1)输入原始信号xs,观测矩阵A,一维观测量b,最大迭代次数,ε>0,调整频率j>0,Δ阈值δ1和δ2,调节参数a<1,c>1. (2)当k小于等于最大迭代次数时,通过迭代式(6)继续迭代. (4)当迭代步k等于j的整数倍时,根据自适应罚参数调整准则更新罚参数;即每经过j步,则更新一次罚参数.以更新的罚参数βk+1返回步骤(2)继续迭代. 本章通过实验分别对不同参数的影响做出分析,总结出一个快速鲁棒的参数选取方案;再根据得出的方案,做出比较实验,通过设置不同的罚参数初始值观察本文方法的鲁棒性和有效性. 分别针对调整频率j,Δ阈值,调节参数a、c进行实验,研究不同的参数取值对自适应罚参数调整准则的影响. 由于罚参数过大或过小都会影响信号的恢复质量,因此将罚参数设置为βk∈[5×10-5,50].此外,取ε=5×10-4,最大迭代次数为9 999. 下面通过3组实验详细研究准则中的不同参数对本文方法效率的影响. 3.1.1 调整频率对本文方法的影响 自适应罚参数调整准则中的频率j表示根据每j步的信息计算准则中的各个值.本次实验分别取j=5,10,20,30,实验结果见表1. 表1 不同调整频率下的恢复效果指标Tab.1 Recovery effect indicators with different adjustment frequencies 从表1可以看出,罚参数自适应调整频率的改变主要影响本文方法的运行速度,随着调整频率的增大,达到终止条件需要的迭代次数变多,从而运行时间变长.从表中很容易看出j=5时,本文方法所需的迭代次数和迭代时间最少,但是从所得解的质量情况来看,并不是最好的.因此,综合考虑,选取j=10为自适应罚参数调整准则中j的默认取值. 3.1.2Δ阈值对本文方法的影响Δ阈值决定达到什么样的条件才进行罚参数的调整,间接影响罚参数的调整频率,因此也被作为重要参数之一.对很多组不同的Δ阈值进行了实验,本文仅列举其中的4组实验,结果见表2. 表2 不同阈值下的恢复效果指标Tab.2 Recovery effect indicators with different thresholds 根据本节实验结果,从所需的迭代次数和解的质量等方面综合考虑,选取Δ阈值[1/15,1/10]为自适应罚参数调整准则的缺省值. 3.1.3 调节参数对本文方法的影响 除了调整频率、Δ阈值外,调节参数a<1,c>1决定了每次罚参数调整的大小,也是影响罚参数自适应调整的一个重要因素.因此,在本实验中,设置不同的调节参数a、c,分析其对信号恢复效果的影响.部分实验结果见表3. 表3 不同调节参数下的恢复效果指标Tab.3 Recovery effect indicators with different adjustment parameters 根据本节实验结果,可以看出本文方法对调节参数的大小不十分敏感.这也意味着本文所提出的自适应罚参数调整准则符合罚参数在本文方法迭代中的意义.选择数值效果较好的a=0.9,c=2.00作为本文方法的默认取值. 综上所述,自适应罚参数ADM选取的默认参数方案:调节频率j=10,Δ阈值为[1/15,1/10],a=0.9,c=2.00.需要指出的是,本文方法的参数取值是经过大量数值实验(本文只列举了一组)得到的,一般不需要再次调试. 本文方法是在程序包YALL1的基础上改进的,YALL1是基于l1对偶问题的ADM框架(即迭代式(6))编写的Matlab程序,具体可参考文献[16].为了验证本文方法的鲁棒性和有效性,在本例中设定不同量级的初始罚参数取值,对YALL1算法和本文方法所得的恢复效果指标进行对比,见表4. 表4 不同罚参数初始值下的恢复效果指标Tab.4 Recovery effect indicators with different penalty parameter initial values 表4表明:(1)对于YALL1算法,当罚参数初始值很小时,原始问题约束条件得到很好的满足,但对偶问题的约束并未满足(约束函数值达到102),因此其恢复效果(e值)较差.当罚参数初始值很大时,由于YALL1算法中对于罚参数较大的情形给出了一种减小罚参数的调整方案,因此,可以看到其恢复效果较好(相对误差达到10-3),但原始问题和对偶问题的约束条件满足的精度仍然较低.(2)对于本文方法,无论初始罚参数取值过大或过小,其恢复效果都能够达到10-3的误差,并且原始问题和对偶问题的约束条件满足的精度都较高,对偶间隙相对差都能达到10-4.(3)与YALL1算法较好的结果相比(第4、5组),由于自适应罚参数的动态调整,不仅所得解的性态更好,还使得本文方法的迭代次数更少,加快了运行速度. 为了更加直观地比较YALL1算法与本文方法,以初始罚参数β为例,画出原始问题和对偶问题目标函数值h随迭代次数i的变化曲线,如图1所示. 图1 原始-对偶问题的目标函数值随迭代 次数的变化Fig.1 The value of the objective function of the primal- dual problem varing with the number of iterations 为了进一步说明本文方法的有效性,将本文方法、YALL1算法、高效近块坐标同伦算法[5]进行对比.本实验数据采用Matlab随机生成的m×n矩阵A、加噪声的b,以及长度n、稀疏度v的原始稀疏信号xs(利用KKT条件生成的真实信号).高效近块坐标同伦算法[5]和YALL1算法以及本文方法均采用其默认设置.对不同规模的数据进行10次实验,结果见表5.(对所有实验结果取均值) 表5 不同算法下的恢复效果指标Tab.5 Recovery effect indicators with different algorithms 从表5可以看出:(1)对于数据恢复的相对误差,高效近块坐标同伦算法稍好一些,这是因为高效近块坐标同伦算法是基于KKT条件设计的,与生成的原始信号较吻合.另外,由于数据有噪声,本文方法结果在容许范围内.(2)对于约束函数值,3种算法的结果都在精度范围内.(3)对于迭代步数,由于高效近块坐标同伦算法是将大规模问题分解成一系列小规模问题,期间滤除了大部分零分量,并且是基于KKT条件进行更新迭代,因此大大减少了迭代步数.(4)对于迭代时间,虽然高效近块坐标同伦算法迭代步数很少,但每次迭代需要求解大量不同规模的线性方程组,因此用时较多.而本文方法在时间上优势明显,从数值实验上验证了自适应调整罚参数对YALL1算法的改进成效. 本文研究了求解压缩感知中的l1极小化问题的ADM,在经典ADM框架基础上,提出了一种自适应罚参数交替方向法.通过平衡目标函数下降速度和约束条件的满足程度,对罚参数进行动态调整,进而使得信号恢复得快速、准确.本文方法在一定程度上放松了对初始罚参数的范围要求,加速了经典ADM.下一步,将研究如何将本文方法推广到带有罚参数的实际优化问题.1 l1问题的ADM
1.1 经典的ADM


1.2 应用ADM于原始问题
1.3 应用ADM于对偶问题


2 罚参数自适应调整
2.1 罚参数分析
2.2 自适应罚参数ADM

3 数值实验

3.1 通过实验获得参数方案




3.2 验证本文方法的鲁棒性和有效性


4 结 语

