开放对流环境下合作反应扩散对流模型的解的全局定性分析①
刘青兰,张国洪
西南大学 数学与统计学院, 重庆 400715
种群之间互惠共生是自然界中一种常见的生态学关系. 许多数学家和生态学家提出了不同的数学模型来刻画物种之间相互合作的关系[1-2]. 特别地, 文献[3]提出了下列合作互惠模型:
(1)
其中:u和v代表两个合作种群的密度,ai(i=1,2)代表种群内在增长率,a1c1和a2c2代表种群内竞争系数, 物种u和v的环境容纳量分别为K1+b1v和K2+b2u, 可以看出其中一个种群的存在有利于另一个种群的生长, 系数ai,bi,ci和Ki(i=1,2)都是正常数. Albrecht证明了系统(1)存在唯一全局渐近稳定的正稳态解. 在模型(1)的基础上, 文献[4-6]考虑了扩散和交叉扩散条件下系统非常数正平衡解的存在性问题; 文献[7-8]则进一步研究了两个互惠种群在自由边界条件下是否能够入侵的条件.
近年来, 对流环境中的种群动力学行为得到了大量的研究, 如河流中的相互竞争种群、 捕食-食饵种群, 相应的动力学模型一般为反应扩散对流模型. 研究发现对流的引入对相互竞争种群及捕食食饵系统的动力学行为有重要的影响[9-11]. 基于上述分析, 一个自然的问题就是对流的引入对以上互惠共生种群模型(1)的动力学行为有什么影响, 即研究下列反应-扩散-对流合作模型:
(2)
其中:u(x,t)和v(x,t)是两个互惠物种的种群密度;ai,bi,ci,Ki(i=1,2)的意义与系统(1)相同; 正常数d1,d2代表扩散系数,q1,q2代表两个种群非负的对流速率;L是栖息地的大小. 在上游x=0处, 我们假设物种满足无通量边界条件, 这意味着不允许任何个体通过该边界. 在下游x=L处, 我们假设为自由流边界条件, 在文献[12]中, 该边界条件被称为Danckwerks边界条件, 它用来刻画小溪流向湖泊的自然情况.
1 系统的耗散性
本节将证明系统(2)存在唯一一个正解, 它对所有的x∈[0,L]和t>0都有界.
定理1对任意非负非平凡初值函数(u0(x),v0(x)), 系统(2)都有唯一一个非负解(u(x,t),v(x,t)), 且存在两个仅依赖初值(u0(x),v0(x))的正常数M1,M2使得
0
证首先, 由强极大值原理可得u(x,t)>0以及v(x,t)>0. 然后取正常数M1和M2使得
则容易验证(M1,M2)和(0, 0)是系统(2)的一对有序的上下解. 由文献[14]的定理8.3.1得系统(2)在S(0, 0;M1,M2)上有唯一解, 其中
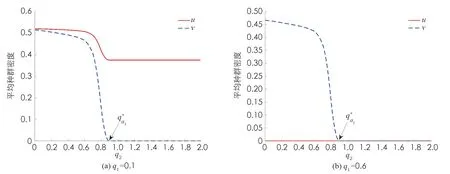
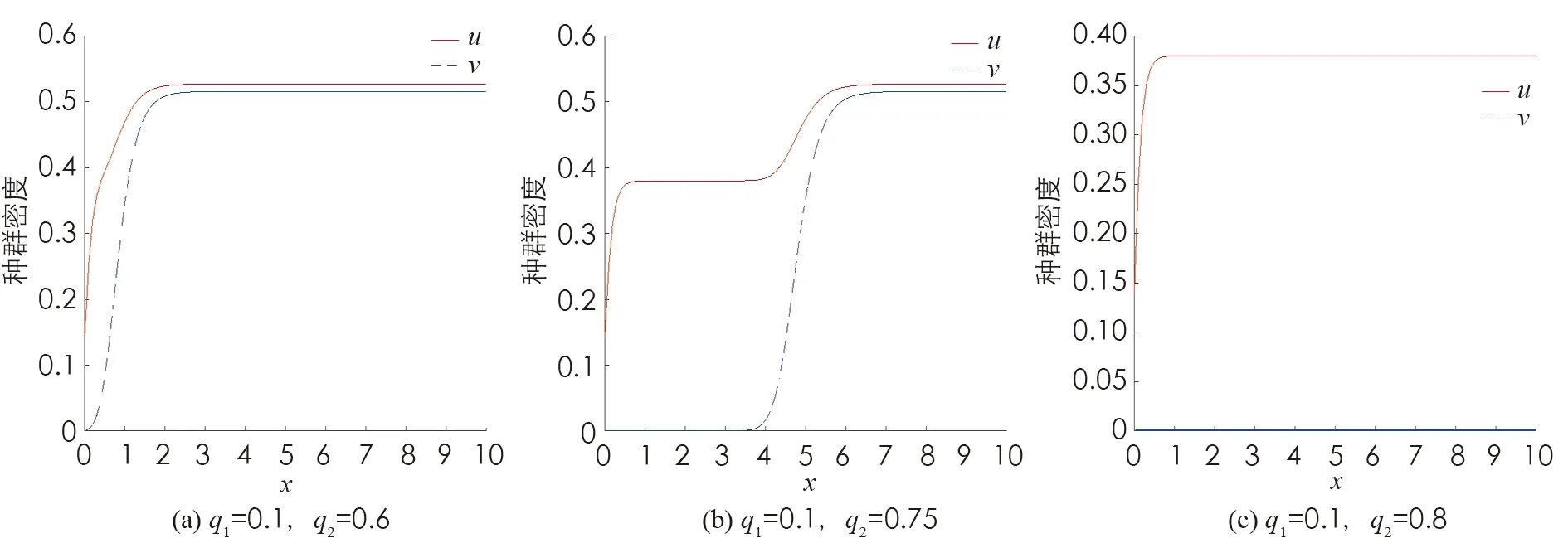
S(0, 0;M1,M2)={(u,v)∈C([0,L]×[0, +∞)); 0 定理证毕. 本节研究系统(2)的平衡态解的存在性和稳定性. 我们首先回顾以下单种群模型的相关结论: (3) 以及 (4) 与(3)式相应的特征值问题如下: (5) (6) (7) 其中:λ1(q2,a2)是(5)式中d1,q1,a1被d2,q2,a2替代后的系统的主特征值. 由文献[9]的定理2.1(b)可得单种群模型(3)和(4)的如下结果. 证我们首先证明半平凡稳态解(0,θq2)是局部渐近稳定的. 为此, 把(2)式对应的稳态系统在(0,θq2)处线性化, 可以得到如下相应的特征值问题: (8) 接下来证明在非负和非平凡初始条件下, 系统(2)的解(u(x,t),v(x,t))收敛到(0,θq2). 由抛物方程的极大值原理可得系统(2)的解(u(x,t),v(x,t))对所有x∈[0,L]和t>0, 都满足u(x,t)>0,v(x,t)>0. 因此, 在(0,L)×(0, +∞)上, ut≤d1uxx-q1ux+a1u 从而由抛物方程的比较原理可推出对任意x∈[0,L]和t>0, 有u(x,t)≤U(x,t), 其中U(x,t)满足 即对任意的ε>0, 存在T1>0, 使得对所有的x∈[0,L]和t>T1, 都有u(x,t)<ε. 故在(0,L)×(T1, +∞)上 (9) (10) 同时, 由(9)式右边不等式以及抛物方程比较原理可得对x∈[0,L]和t>T1, 有v(x,t)≤Vε(x,t), 其中Vε(x,t)满足 (11) 证为了证明半平凡稳态解(θq1, 0)是局部渐近稳定的, 把(2)式对应的稳态系统在(θq1, 0) 处线性化, 可以得到如下相应的特征值问题: (12) 证首先证明系统(2)的平凡稳态解(0, 0)是局部渐近稳定的. 事实上, 只需考虑以下特征值问题: (13) 本节致力于研究初始条件为u(x, 0)=u0(x)(u0(x)≥0且u0(x)≢0)和v(x, 0)=v0(x)(v0(x)≥0且v0(x)≢0)时系统(2)的解(u(x,t),v(x,t))的一致持续性. 证我们使用抽象持久性理论[15]来证明这个定理. 首先定义Θ(t)是状态空间P上系统(2)的解半流, 其中在[0,L]上, P={(u,v)∈C[0,L]×C[0,L]:u≥0,v≥0} 令P0={(u,v)∈P:u(x)≢0,v(x)≢0}, ∂P0=PP0. 由极大值原理可得若(u0,v0)∈P0, 则对任意的x∈[0,L]和t>0, 系统(2)的解都满足u(x,t)>0,v(x,t)>0. 因此,P0在P中是开的, 且在系统(2)生成的动力学下是前向不变的, 即对所有t≥0, 有Θ(t)P0⊆P0. 再者, ∂P0包含平衡点(0, 0), (θq1, 0)和(0,θq2). 剩下的证明分为以下5个步骤. 1) 令M∂={(u0,v0)∈∂P0:Θ(t)(u0,v0)∈∂P0, ∀t≥0},ω((u0,v0))是正向轨道γ+((u0,v0))={Θ(t)(u0,v0) :t≥0}的ω极限集. 先证明 2) 证明(0, 0)是一致的弱排斥子, 即存在δ1>0, 使得对任意的(u0,v0)∈P0, 都有 (14) 由比较原理得出对任意的t≥t0,x∈[0,L], 有 3) 证明(θq1, 0)是一致的弱排斥子, 即存在δ2>0, 使得对任意的(u0,v0)∈P0, 都有 (15) ‖u(x,t, (u0,v0))-θq1‖<δ, ‖v(x,t, (u0,v0))‖<δ 从比较原理得出对任意t≥t1,x∈[0,L], 有 4) 证明(0,θq2)是一致的弱排斥子, 它是P中的孤立不变集. 这个证明类似于第3步, 此处省略. 其中Ws({(0, 0)}),Ws({(θq1, 0)})和Ws({(0,θq2)})分别是(0, 0),(θq1, 0)和(0,θq2)的稳定集[15]. 因此{(0, 0)}∪{(θq1, 0)}∪{(0,θq2)}的子集在∂P0中没有形成一个圈. 从而由文献[15]的定理3可得: 存在η>0, 使得对任意的(u0,v0)∈P0, 有 本节通过数值模拟研究对流速率对系统(2)动力学行为及种群空间分布的影响. 由前面的理论分析已经知道两个共生种群的对流速率q1,q2对系统(2)的动力学行为有很大的影响. 取d1=0.01,d2=0.02,a1=2,a2=3,K1=0.4,K2=0.5,b1=0.3,b2=0.1,c1=0.1,c2=0.2和L=10, 并通过改变q1,q2的值来观察系统(2)的各种动力学性态的变化. 图1 对流速率q2对系统(2)动力学性态的影响 接下来, 我们关注对流速率对种群在河流[0,L]中密度分布的影响. 先固定对流速率q1, 然后取不同的q2来观察这两个共生物种在河流[0,L]中的分布情况. 通过数值模拟发现, 当对流速率q2很小时, 两个物种共存, 且在整条河流都有分布(图2(a)). 当对流速率q2逐渐增大时, 两个物种仍然可以共存, 但种群v已经被冲到河流下游, 生存区域变小, 导致平均密度降低, 同时使得互惠种群u的平均密度也降低(图2(b)). 当对流速率q2足够大时, 物种v将灭绝(图2(c)). 对流速率q1的变化对两个种群的密度分布影响是相似的, 在此不再赘述. 图2 对流速率q2对系统(2)的种群密度分布的影响2 种群的灭绝性

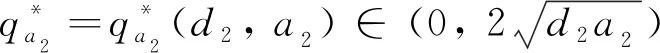










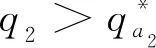


3 一致持续性
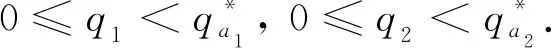



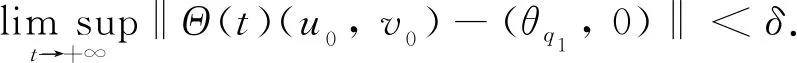






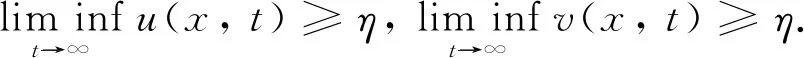
4 数值模拟

5 结论及讨论


