基于条件高斯分布的未知输入与状态估计算法

丁 博 ，杨月全，方华京

(1.扬州大学信息工程学院自动化专业部，江苏扬州 225127;2.华中科技大学人工智能与自动化学院，湖北武汉 430074)

1 引言

未知输入和状态估计算法在地球物理和环境应用[1]、故障估计[2]以及容错控制[3]等领域有着广泛的应用，受到了诸多研究者的关注.

对于未知输入仅出现在系统方程的线性随机系统，最小方差无偏(minimum-variance unbiased，MVU)算法是估计未知输入和状态的一种通用算法[1].随后，研究者们利用参数化方法推广了MVU算法[4-6].文献[7]和文献[8]分别给出了MVU算法的全局最优性和稳定性.文献[9]给出了一种基于多步信息的输入和状态同步估计方法，减少了噪声的敏感性.

针对直接馈通系统，即未知输入同时影响状态方程和测量方程的系统，文献[10]提出了递归3步滤波算法(recursive three-step filter，RTSF)来估计系统的未知输入和状态.对于直接馈通矩阵不满秩的情况，文献[11-13]利用奇异值分解的方法来改进相应的算法.但是，这种方法仅能得到系统的状态估计而忽略了未知输入估计，为此，文献[14]和文献[15]分别提出了5步递归滤波算法来得到未知输入估计.值得注意的是，上述文献中提到的算法都是在输入信息完全未知的情况下得到的.最近，文献[16]指出RTSF算法需要系统满足强可检测性(strong detectability)条件，如果系统不满足强可检测性条件，则RTSF算法将发散.这在一定程度上限制了该算法的应用.然而，文献[16]只讨论了如何构造出满足强可检测性的模型，但并没有给出相应的滤波算法.文献[17]将有限方差的高斯分布做为未知输入的模型，为未知输入估计算法的设计提出了一个新的思路.

受到文献[17]的启发，本文针对直接馈通线性随机系统，采用有限方差的高斯分布作为未知输入的模型[17]，根据条件高斯分布的性质，推导出一个新的算法来得到未知输入估计和状态估计.本算法的贡献主要由以下两点:1)利用矩阵极限的性质，从理论上严格证明了当未知输入模型的方差趋于无穷大时，本文给出的滤波公式等价于文献[10]提出的RTSF算法，也即，RTSF算法相当于是本文算法中当未知输入模型的方差趋于无穷大时的特例;2)给出了本文提出的滤波公式的稳定性条件.结果表明，与RTSF算法相比，本文给出的滤波算法不需要强可检测性条件，因而适用性更广.

2 问题描述和RTSF算法

本节，本文给出直接馈通随机系统的数学模型，并简要介绍文献[10]提出的RTSF算法.

2.1 问题描述

考虑如下直接馈通线性随机系统:

初始值分别与系统噪声wk和测量噪声vk互不相关.

注1为表述简明起见，本文只考虑时不变系统.应当指出的是，本文的算法对于时变系统仍然成立.

2.2 RTSF算法

在没有未知输入dk的先验信息的条件下，可以利用RTSF算法[10]来得到未知输入的估计和状态估计.接下来对该算法作一简要介绍，更多细节请参考文献[10].步骤1时间更新:

步骤2未知输入估计:

步骤3状态估计:

3 滤波推导

本节，本文采用有限方差的高斯分布来描述输入信号dk，以此作为辅助信息，利用条件高斯分布的性质，推导出模型(1)的滤波公式，进而得到系统的未知输入估计和状态估计.

假 设1[17]令dk～N(σ，Qd)，(k ＞0)，并且与初始值x0，d0以及噪声wk，vk互不相关.

根据上述假设，结合系统(1)的模型，利用高斯分布的条件概率密度，得到下述算法.

则k时刻的估计及协方差矩阵可由下列表达式得到

其中Pk|k-1和Γk分别由式(17)-(18)给定.再根据高斯分布的条件概率密度公式，可以得到条件期望为

整理即得式(19)-(22).同时由式(27)可知xk和dk的协方差为

注2RTSF算法(2)-(12)是在输入dk的信息完全未知的情况下直接由系统(1)推导得到的，其推导过程并没有用到任何未知输入的信息.而本节的算法(16)-(26)的推导则借助了dk的信息.应当指出的是，假设1中dk的信息蕴含在其方差Qd之中.而当(Qd)-1→0时，也就意味着dk的信息趋于未知.此时，算法(16)-(26)的结果应当趋近于RTSF算法.接下来，本文将利用矩阵极限的工具，严格证明上述结论，即，当(Qd)-1→0时，算法(16)-(26)等价于RTSF算法(2)-(12).

4 等价性证明

本节，本文将证明本文给出的滤波式(16)-(26)在极限情况下，即当(Qd)-1→0时，等价于RTSF算法(2)-(12).在给出主要结论之前，首先给出了如下引理.

引理1(矩阵逆引理[18]) 设A，B，C，D是具有适当维数的矩阵，其中A和D都是可逆的.如果(A+BD-1C)和(D+CA-1B)也可逆，那么以下式子成立:

引理2设矩阵Qd ∈Rq×q，R ∈Rm×m，H ∈Rm×q，其中Qd和R是正定的，rankHq，m≥q.当(Qd)-1→0时，则以下式子成立:

证由于rankHq，且R是正定的，显然可知((Qd)-1+HTR-1H)-1存在.利用式(28)可得

由此可知式(32)与式(30)成立.根据式(29)，可得于是式(31)成立. 证毕.

定理2如果定理1中的滤波式(16)-(26)与RTSF算法(2)-(12)在第(k-1)步时的协方差矩阵相等，也即

则当(Qd)-1→0时，有MkMk，LkLk，且两种滤波在第k步时的协方差矩阵也相等，即

证明过程参见附录.

注意到式(21)-(22)可以重新表示为

由式(13)-(14)和定理2可得，当(Qd)-1→0时，下面式子成立:

于是式(35)-(36)分别退化为式(10)和式(6).根据以上的讨论，可以马上得到下述定理.

定理3对于直接馈通线性随机系统(1)，如果初始协方差满足

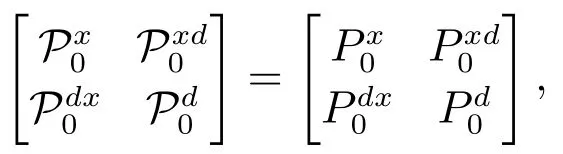
则当(Qd)-1→0时，滤波式(16)-(26)与RTSF算法(2)-(12)等价.

仿石器材光学性能测试主要测试表面光谱反射曲线，与真实光谱进行对比，计算其差值，看是否满足伪装要求。测量采用ISI921VF-512型野外光谱仪，其主要技术指标见表1。

注3本节严格证明了，当(Qd)-1→0时，算法(16)-(26)等价于RTSF算法(2)-(12).从这个意义上说，RTSF算法相当于是本文给出的算法在(Qd)-1→0时一个极限.同时由定理3可知，即使未知输入的信息完全未知，也可以通过选取一个适当的Qd，利用滤波公式(16)-(26)来近似代替RTSF算法.

5 渐近稳定性

本节，本文将讨论滤波式(16)-(26)的渐近稳定特性.考虑线性时不变随机系统(1)，令

则(18)式中的Γk可以改写为

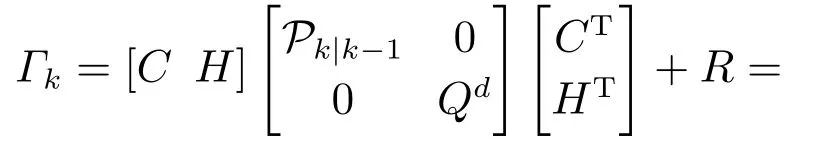
再由式(23)-(26)，可得

根据式(17)及式(39)可得到矩阵黎卡提方程如下:

下面将讨论式(40)的矩阵序列的收敛条件，首先给出两个预备引理.

引理3(A，C)是可检测的(detectable)，当且仅当(A，C)可检测.

证明过程参见附录.

同理可以得到下述引理.

由于强可检测性条件(41)不满足，RTSF算法将不能使用.但是(A，C)可检测，则由定理4可知，本文的算法依然适用，因此可以选取一个适当的Qd，利用本文提出的滤波算法来估计系统的状态.

注5由定理2和定理3可知，当(Qd)-1→0时，滤波式(16)-(26)等价于RTSF算法.但是，由定理4可知，两者的稳定性条件并不完全一致.由此可以间接地得知，当强可检测性条件不满足时，随着(Qd)-1→0，矩阵黎卡提方程(40)的解将不再收敛.

6 仿真结果

本节，本文将通过仿真，来说明滤波当(Qd)-1→0时，滤波式(16)-(26)与RTSF算法(2)-(12)的等价性.并讨论当强可检测性不满足时，两个算法的差别.

例1考虑如下一维模型:

其中系统噪声的方差为Q0.01，测量噪声的方差为R0.1.初始状态值为0.1，其初始方差为1.未知输入为周期30 s，幅值0.25的正弦波.利用RTSF算法，可以得到滤波的稳态值为M1，L0.状态估计和未知输入估计误差的方差分别为Px0.11，Pd0.21，其协方差误差为Pxd-0.11.

下面考虑本文的算法(16)-(26)，令σ0，针对不同的Qd，可以得到相应的滤波增益矩阵和滤波结果，如表1中所示.

表1 不同Qd值下本文算法的结果Table 1 The result of the proposed filter with different value of Qd

可以看出，当Qd越来越大时，本文算法的结果趋近于RTSF算法，从而验证了定理2和定理3的正确性.这也说明了，在应用时可以根据系统的实际情况，选取合适的Qd，利用本文提出的算法来近似替代RTSF算法.从理论上说，Qd越大，则本文算法结果越接近于RTSF算法，但Qd的值特别大时可能会导致数值计算溢出的风险.因此，在确定Qd的值时，还需考虑系统模型和硬件情况.

利用RTSF算法，可以得到系统的状态估计，其估计误差如图1所示，这里的估计误差为状态真实值与估计值之差的绝对值，即，ek|xk-|.可以发现，由于强可检测性条件(41)不满足，第1个状态的估计误差发散，此时RTSF算法失效.

图1 RTSF算法的状态估计误差Fig.1 State estimation error by RTSF algorithm

令σ0，Qd1，根据本文提出的滤波式(16)-(26)，可以得到系统的状态估计，估计误差如图2所示，可以看出此时系统的状态估计误差仍是有界的.

图2 本文算法的状态估计误差Fig.2 State estimation error by the proposed algorithm

显然，与RTSF算法相比，本文提出的算法的适用性更广.在强可检测性不满足时，RTSF算法失效，但仍然可以利用本文提出的算法来得到系统的状态估计，只需选择一个合适的Qd即可.应当注意的是，此时状态估计误差会随着Qd的增大而增大，在实际应用时，需要根据实际情况及滤波精度的要求予以选择.

7 结论

本文主要研究了直接馈通线性随机系统的未知输入估计和状态估计问题.通过采用方差有限的高斯分布作为未知输入信号的模型，以此推导出一个新的滤波算法.并利用矩阵极限的方法，从理论上证明了当输入信号的方差趋于无穷大时，本文给出的滤波算法等价于文献[10]中的RTSF算法.该结论说明了RTSF算法相当于是本文算法在输入信号的方差趋于无穷大时的极限.进一步地，本文详细研究了本文提出的滤波算法的渐进稳定性，在理论上说明了该算法有更广的适用范围.应当指出的是，本文给出的矩阵极限的方法亦可以应用于一般的带有未知输入的线性随机系统，如文献[17]的证明.对于非线性滤波[20]乃至更一般的贝叶斯滤波，如何利用未知输入模型建立相应的融合滤波算法，并探讨其极限性质，有待进一步研究.

附录

定理2的证明如果式(33)成立，则由式(3)和式(17)得Pk|k-1=Pk|k-1，于是Γk可以改写为

将式(A1)分别代入式(19)-(20)，由引理2可得

由此可知当(Qd)-1→0时，有Mk=Mk，Lk=Lk.

同理，当(Qd)-1→0 时，下列等式成立:

这就证明了式(34)成立. 证毕.

引理3的证明假设(A，C)不可检测，则存在z1∈C且|z1|≥1，使得

于是有(z1In-A)β1-Gβ2=0，Cβ1+Hβ2=0，z1Iqβ2=0.又因为|z1|≥1，因此必有β2=0.这样就得到(z1In -A)β1=0，Cβ1=0，也即

所以

这表明(A，C)也不可检测.同理可得，如果(A，C)不可检测，则(A，C)也不可检测. 证毕.