“硬”边界低阶导数型物理信息神经网络:一种流动求解器

流体的流动在自然界和工业过程中无处不在,精确模拟流体流动过程对航空航天

、建筑环境

、能源电力

和生物医学工程

等领域有重要意义。流体流动问题的传统数值模拟通常使用有限差分法、有限容积法或有限元法等方法以离散的形式求解Navier-Stokes(N-S)方程,此即计算流体动力学(computational fluid dynamics,CFD)方法。对于在复杂几何结构中的流动和湍流问题,CFD方法计算过程繁琐,并且在使用过程中对计算区域的网格划分也消耗巨大的计算资源。此外,对于病态问题和反演问题的求解,CFD方法也存在一定的困难。

近年来随着计算机技术和人工智能的发展,深度神经网络以其强大的复杂非线性系统建模能力在计算流体动力学领域引起广泛关注

。深度神经网络在求解流动问题时只需事先获取部分流场数据,然后就可以快速实现对整个计算区域内流场的精准预测。Jin等利用CFD数据集训练了一个可以精确预测不同雷诺数下圆柱绕流流场的卷积神经网络(convolutional neural network,CNN)模型

。谢晨月等基于高马赫数的可压缩湍流直接数值模拟数据训练了一个用于对强可压缩湍流进行大涡模拟的空间人工神经网络模型(space artificial neural network,SANN)

;模拟结果表明,SANN模型展现了优异的预测性能,突破了梯度模型、待定系数梯度模型和反卷积模型的局限性,此外,Kim等建立了一个通过输入壁面切应力等壁面信息就可以实现对湍流通道局部热通量进行精确预测的CNN模型

。以上研究表明,CNN、SANN等深度神经网络模型的优势在于非线性预测能力强、无需划分网格、训练速度快,但是深度神经网络在使用过程中需要事先获取大量的标签数据用于训练网络,而在实际应用过程中获取标签数据往往十分困难。

Raissi等于2017年首次提出了一种名为物理信息神经网络(physics informed neural network,PINN)的新型神经网络框架,该框架通过将控制方程嵌入到传统神经网络中,使其成为一种懂物理的神经网络。研究表明,PINN具有极强的求解/识别偏微分方程的能力

。PINN也可用于流体动力学问题的数值模拟,通过给定控制方程和相应的初始及边界条件即可获得方程的数值结果;且在求解过程中只需从区域内抽取一定数量的残差点,而无需对计算区域进行网格划分。Jin等基于N-S方程和涡量方程,建立了可用于预测流场的速度压力PINN模型和涡量速度PINN模型

。侯龙锋等发现利用

-epsilon雷诺平均N-S方程构建的PINN框架可实现对湍流流动的数值模拟

。Cai等应用PINN求解了一些CFD方法不易解决的病态流动和传热问题

,此外,Cai等利用PINN求解反演问题的能力提出了一种基于实验温度数据预测整个计算区域流场和温度场的PINN模型,这有望为实验流体动力学提供新的发展方向

。然而,与CNN、SANN等深度神经网络模型相比,PINN的劣势在于其训练过程通常需要花费大量时间。因此,如何加速PINN的训练过程成为PINN应用道路上亟待解决的问题。Sun等将边界条件以一种“硬”方式编码到PINN中,提出了“硬”边界物理信息神经网络(“hard”boundary PINN,HPINN)框架;结果表明,HPINN可以有效加速PINN的训练过程,并可在一定程度上提高计算精度

。Zhu等利用赫维赛德函数对PINN施加“硬”边界条件,也可实现对PINN训练过程的加速

。Rao等提出了一种用于模拟不可压缩层流流动的混合变量物理信息神经网络,通过将流函数作为神经网络的输出,该网络自动满足连续性方程,因此可在一定程度上加速网络的训练过程

。

常规双心钻头普遍存在扩孔钻进效率低、扩孔能力差、扩孔后井径不规则、扭矩波动幅度大、横向不平衡力幅值大等问题，难以适应深井定向随钻扩孔钻进[3-5]。其中，常规双心钻头的总体横向不平衡力常常超过钻头轴向力的20%[2,6-7]，在钻井过程中会导致钻头领眼段切削齿磨损严重不均匀，而个别切削齿的提前失效会影响钻头的径向布齿，降低钻头的切削效率，致使钻头领眼段切削齿的寿命提前终结。因此，需增强钻头的稳定性以提高钻头的钻进效率。本文将对定向随钻扩孔PDC钻头结构优化设计展开相关研究，以提高其稳定性。

上述研究主要是通过减少PINN损失函数的损失项数实现对PINN训练过程的加速,这种方式的加速效果有限。本研究另辟蹊径,从控制方程入手,将N-S方程转换成低阶导数形式,转换后N-S方程构建的PINN的损失函数形式简单,易于优化;在此基础上,进一步对PINN施加“硬”边界条件。因此,新的PINN结合了两种方式的优点,其训练过程被大幅加速。本文以求解变截面管道内的流动问题为例,讨论所提出的PINN相较于传统HPINN的训练加速性能以及模拟的精确性。

1 控制方程和神经网络框架构建

1.1 控制方程

二维稳态不可压缩层流流动由下列连续性方程和N-S方程控制

(1)

(2)

传统的通过径向振动信号诊断转轴裂纹的方法中，最有效的就是监测对比转子过1/2、1/3等临界转速时的1、2、3倍频信号幅值改变程度和观察对比转子临界转速的改变量，也就是轴裂纹的径向振动信号特征，只有在机组启停机转子升降速时才有明显的表现，但是石化等流程企业中运行的大型机组，通常运行周期多在一年以上，中途不会为了检查转子裂纹而做停机升降速试验，这样对企业来说少则是几百万元、多则是数千万元的损失，而转子轴的裂纹从生成到扩展断裂，时间就短得多，因此就需要有一个新的方法，在转速变化不大的正常运转中，监测诊断转子轴裂纹的生成与扩展。

1.3 统计学分析 本研究所有数据均采用统计学软件SPSS 21.0进行分析，计量资料采用进行描述，行t检验；计数资料借助率(%)来描述，行χ2检验。生存曲线评估采用Kaplan-Meier法，组间比较采用Log-rank法。P<0.05差异有统计学意义。

1.2 HPINN框架

PINN框架主要由一个全连接神经网络(fully connected neural network,FCNN)和一个残差网络构成。FCNN用于近似N-S方程的解,即FCNN的输入为空间变量(

,

),输出为(

,

,

)。残差网络用于计算控制方程残差。在构建残差网络时,需要计算FCNN的输出变量关于输入变量的偏导数,这可由自动微分技术实现

。FCNN的激活函数采用tanh函数,权重

和偏置

采用Xavier方式进行初始化

。优化策略为先采用自适应矩估计(adaptive moment estimation,Adam)算法进行一定步数的优化

,随后采用局部极小化(limited-memory BFGS-Bound,L-BFGS-B)算法进行更精细的优化

。在计算过程中,通过两种优化算法不断对PINN的损失函数进行优化,从而更新权重

和偏置

,以使PINN可以精准地预测N-S方程的解。当损失函数被优化到一个极小值时,此时的PINN便可以精准预测N-S方程的解。

(3)

其中

(4)

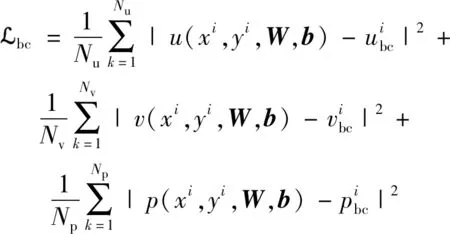
(5)

1)不同微物理参数化方案的选择对降水预报有一定的影响,通过对这12次个例的统计评估,发现在这些个例中对小雨和暴雨预报较好,而中雨和大雨预报较差。对于24 h累积降水,8种方案都可预报出雨带的大致位置以及强降水中心,但是预报的强降水中心强度偏大,并且普遍存在小雨空报的问题。综合RMSE、ACC和TS评分的结果发现,对于24 h累积降水,CAM5.1方案较优,Morrison 2-mom方案次之,NSSL 2-mom方案最差。对于3 h、6 h累积降水,同样可以发现CAM5.1方案较优,并且当预报时效为12 h和36 h时,模式预报的效果较好。

上述这种将边界条件以数据误差的形式添加到损失函数中,构建有约束优化损失函数的方式称之为“软”边界条件。以这种“软”方式构建的损失函数进行训练主要有两种弊端。一是该损失函数中

的大小会对PINN的预测性能产生严重影响。若

较小则会导致PINN预测结果可以很好地满足控制方程,但是却不能精确满足边界条件,致使计算结果不准确,反之亦然;而通常惩罚系数的选择只能依靠经验和反复尝试。二是在求解具有复杂几何结构的问题时,特别是边界发生突变的问题时,“软”方式不能精准施加边界条件,PINN在计算时难以预测边界的形状规律,导致最终的计算误差较大。

为规避以上两种弊端,本研究采用“硬”边界条件进行计算。“硬”边界条件是通过利用边界条件和距离函数强制使PINN满足相应的边界条件。“硬”边界PINN的输出变量可由下列公式表示

在罐区设置紧急切断阀、构建安全联锁保护系统对于维护罐区安全生产，保护人员生命及财产安全等具有十分重要的意义，设计人员应做好紧急切断阀的选型及安全联锁保护设计等工作，并在应用过程中通过不断地探讨与改进，使其应用更加合理化、规范化，充分发挥其在罐区安全保护方面的积极作用。

=

[1-

(

,

)]+

(

,

)

(6)

=

[1-

(

,

)]+

(

,

)

(7)

=

[1-

(

,

)]+

(

,

)

(8)

式中:

、

和

为“硬”边界PINN的输出变量;

、

和

为FCNN的直接输出变量;

、

和

为给定的第一类边界条件;

(

,

)为与点(

,

)到边界的距离有关的连续光滑函数,当点(

,

)在边界上时

(

,

)=0,当点(

,

)远离边界时

(

,

)≠0,且越远离边界其值也越大。

以这种“硬”方式施加边界条件可以实现PINN对边界上值的零误差预测,因此相较于“软”边界可以有效提升计算精度。与此同时,“硬”边界PINN的损失函数无需边界条件损失,因此可在一定程度上加速训练过程。用于求解二维稳态不可压缩层流流动问题的“硬”边界物理信息神经网络框架如图1所示,其损失函数如下式所示

首先，德育教师要变知识的灌输者为学习的引导者，增强学生的主体意识，通过讨论式教学、情景式教学、案例教学等方式构建新型课堂教学模式，加强与学生的互动和合作，鼓励学生独立思考、勇于创新，引导学生自我教育、自我管理，自觉将优秀传统文化蕴含的道德理念内化到自己的行动中。其次，德育教师要不断探索师生关系，尊重学生情感和人格，给予学生充分的信任、宽容、理解与支持，善于发掘学生的“闪光点”，因材施教，帮助学生树立自尊、自信、自强、自立、自律的主体观念，使学生更加积极主动地参与到传统文化教学中。

(9)

2.2.1 数值模拟的精确性研究

(10)

1.3 HLPINN框架

(11)

(12)

(13)

式中:

为柯西应力张量。

式中:

=1 m/s,可保证流动为层流。出口压力为0,壁面无滑移。用于施加速度和压力边界条件的距离函数可分别表示如下

以求解二维稳态不可压缩层流问题为例,HLPINN的输入变量仍是空间变量(

,

),输出变量则变为(

,

,

,

)。与HPINN相同,HLPINN的损失函数也只包含控制方程损失,只是控制方程变成了低阶导数的形式。HLPINN的激活函数、初始化方法和优化策略均与HPINN保持一致。用于求解二维稳态不可压缩层流问题的“硬”边界低阶导数型物理信息神经网络框架示意图如图2所示。本文虽只以二维稳态流动问题为例建立HLPINN框架,但是该框架也可非常方便地拓展用于解决更为复杂的问题。例如对于三维非稳态流动问题来说,FCNN输入变量为时空变量(

,

,

,

),输出变量需增加

方向的速度和相应的应力分量,然后将三维非稳态问题的控制方程嵌入残差网络。最后,将初始条件以数据误差的形式添加到损失函数中即可完成构建求解三维非稳态流动问题的HLPINN框架。

2 结果与讨论

变截面管道(截面扩张和收缩)在工业生产过程中应用广泛,例如工业输送管道及管道的阀门连接处;在生物医学工程领域也很普遍,例如狭窄的血管和患有动脉瘤的血管。基于深度学习框架TensorFlow,本文应用所提出的HLPINN和HPINN框架对变截面管道内的流动进行数值模拟,以探究两种框架求解流动问题的有效性,并比较HLPINN相对于HPINN对神经网络训练加速的能力。

为比较HLPINN和HPINN数值模拟的精确性,本研究采用HLPINN和HPINN求得的解与CFD方法求得解的相对误差

进行比较,其计算公式如下

(14)

本文变截面管道的截面半径可由下式表示

=

±

(2π

)

-12

e

-(-)2

(15)

式中:截面扩张时±取正号,反之取负号;

为管道入口半径,固定为0.1 m;

为与截面变化程度有关的参数,其值越大则截面越宽或越窄,固定为0.005 m

;

为截面变化峰值点的位置,固定为0.5 m;

为影响截面变化陡度的参数,固定为0.1 m。

2.1 截面扩张管道内的流动

2.1.1 数值模拟的精确性研究

本节应用HLPINN和HPINN对截面扩张管道的流动问题进行求解。管道长度为1 m,截面半径由式(15)表示。流体的密度

=1 kg/m

,运动黏度

=0.01 m

/s,管道入口处施加抛物线型速度边界条件,具体可由下式描述

(16)

变换形式后,控制方程导数项的最高阶数由二阶降为一阶。利用式(11)、(12)和(13)构建的PINN,由于其损失函数只包含一阶导数,训练过程中的反向传播过程被加速,因此可以大幅节省训练时间。同时,边界条件也采用“硬”方式施加。这种新型PINN框架称之为“硬”边界低阶导数型物理信息神经网络框架(“hard”boundary low-order derivative PINN,HLPINN)。

旅游业是一个综合性产业，涉及餐饮、住宿、交通、游览、购物和娱乐等诸多领域，需要相关行业的支持与配合，同时也离不开冰雪制造业、冰雪教育和科研等领域的支持。

=10

(

-

)

(17)

=-

+1

从PCK的提出到PCKg及TPCs的演变来看，关于PCK的研究体现出以下两个特点：一是研究者的知识观发生了转变，由静态的知识观转向动态建构的知识观；二是PCK不断丰富完善，其内涵更加强调了在PCK形成与发展中个人的意义，特别强调教师的教学建构及在这一过程中的反思.

(18)

由式(17)和(18)可见,

仅在入口和壁面处函数值为0,满足施加速度边界条件的要求。

仅在出口处函数值为0,满足施加压力边界条件的要求。

首先研究不同神经网络大小(隐藏层数×每层神经元数)对HLPINN和HPINN模拟精确性的影响,以期找到表现最佳的神经网络。计算过程中采用拉丁超立方抽样方法从计算区域内抽取

=5 904个残差点,并对壁面附近加密。优化策略为先采用学习率为0.001的Adam算法进行30 000步计算,紧接着采用L-BFGS-B算法进行5 000步计算。所有训练均在同一计算平台(NVIDIA GeForce GTX 1660 GPU,Windows 10 Pro)上完成,每个算例进行3次重复计算。截面扩张工况下不同大小的HLPINN和HPINN预测的

方向速度

的相对误差

如表1所示。

由表1可知,所选12种不同大小的HPINN均能精确模拟截面扩张管道内的

方向速度

,并且将相对误差

控制在0.29%左右。相比之下,HLPINN的误差比HPINN的略大,但是也保持在同一数量级。在所有算例中,HLPINN的最大误差仅为1.11%,表明其能精确模拟管道内的速度分布。HLPINN大小为8×100时的误差最小,下文选用8×100的HLPINN和HPINN的计算结果做进一步讨论。

图3(a)、3(b)和3(c)分别为CFD、HLPINN和HPINN模拟得到的流场情况。由图3可见,HLPINN和HPINN对流场的模拟结果与CFD结果高度一致。这说明两种框架均能精确模拟管道内流场情况。

图4(a)和4(b)分别给出了由HLPINN、HPINN和CFD预测的截面

=0.5 m处的

、

方向速度曲线和沿通道中心线(

=0 m)的压力分布。曲线表明两种框架均可精确模拟截面扩张处流体的

、

方向速度分布以及管道内的非线性压降。

2.1.2 HLPINN的加速性能研究

为深入研究HLPINN的训练加速效果,对比了不同大小HLPINN和HPINN完成训练所需的时间。物理模型及边界条件、残差点数,优化策略与2.1.1小节中的相同。截面扩张工况下不同大小HLPINN和HPINN的训练时间如图5所示。

由图5可见,随着神经网络增大,两种框架的训练时间均随之增加。这是由于当神经网络增大时,其训练所需计算的参数增多导致的。另外,对比曲线可以发现,HLPINN的训练时间比同等大小的HPINN明显大幅缩短,这说明HLPINN对训练过程的加速效果极佳。具体来看,当神经网络大小分别为6×50、6×60、6×70、6×80、6×90和6×100时,HLPINN的训练时间比HPINN分别减少了68.39%、68.24%、66.19%、65.63%、65.97%和63.72%,平均减少了66.36%。同样,当神经网络大小分别为8×50、8×60、8×70、8×80、8×90和8×100时,训练时间分别减少了67.23%、66.71%、65.00%、64.73%、63.89%和62.43%,平均减少了65.00%。

为进一步研究HLPINN加速效果对优化算法的依赖性,比较了Adam和L-BFGS-B两种优化算法的平均计算速度,如图6所示。由图6可见,基于先前同样的原因,两种算法的计算速度均随神经网络的增大而降低。对比曲线可以明显发现,两种算法对HLPINN的计算速度比同等大小的HPINN要快很多。这说明HLPINN对两种算法均有明显的加速效果。具体来看,当隐藏层数为6时,Adam算法对HLPINN的计算速度较其对HPINN的计算速度分别提高了232.14%、231.13%、209.45%、205.27%、210.61%和187.96%,平均提高了212.76%;L-BFGS-B算法对HLPINN的计算速度较其对HPINN的计算速度分别提高了110.55%、108.63%、104.37%、98.72%、91.85%和96.23%,平均提高了101.72%。类似地,当隐藏层数为8时,Adam算法对HLPINN的计算速度较其对HPINN的计算速度平均提高了200.89%;L-BFGS-B算法对HLPINN的计算速度较其对HPINN的计算速度平均提高了98.41%。可见,HLPINN的加速效果明显依赖于优化算法,即Adam算法的加速幅度明显高于L-BFGS-B算法。然而,对于相同大小的同种神经网络,L-BFGS-B算法的计算速度却比Adam算法快,因此在制定优化策略时可以适当减少Adam的迭代步数,并相应增加L-BFGS-B的迭代步数以减少训练时间。

表2测试了6个节点在以上3种情况下系统测得数据与实测数据比较，数据误差小于5%，表明系统能够较准确采集到环境数据，能够满足一般的检测需求。

2.2 截面收缩管道内的流动

其中

本节应用HLPINN和HPINN对截面收缩管道内的流动问题进行求解。管道长度为1 m,截面半径由式(15)表示。流体的物性和管道的边界条件与2.1.1节中相同。用于施加速度和压力边界条件的

、

与式(17)、(18)相同。

同样,首先研究不同神经网络大小对HLPINN和HPINN模拟精确性的影响。残差点数

=5 700,优化策略仍为二段式优化,只是L-BFGS-B算法的计算步数调整为8 000。截面收缩工况下不同大小HLPINN和HPINN预测的速度

的相对误差

如表2所示。

由表2可知,截面收缩工况下所选12种不同大小的HPINN均能将速度

的相对误差

控制在0.27%左右。HLPINN的计算精度虽然比HPINN的低,但是已经可以满足大部分实际需求。最佳的网络大小仍为8×100。

图7(a)、7(b)和7(c)分别为CFD、HLPINN和HPINN对管道内流场的模拟情况。速度、压力云图表明两种神经网络框架均能精确模拟截面收缩管道内的流场情况。

图8(a)和8(b)分别给出了由HLPINN、HPINN、CFD预测的截面

=0.5 m处的

、

方向速度曲线和沿通道中心线(

=0 m)的压力分布。可见,由于截面收缩处流动非线性增强,且

方向速度本身数值较小,HLPINN对截面收缩处

方向速度的预测结果与CFD和HPINN结果相比有些许偏差,但是其对截面收缩处

方向速度分布以及管道沿程非线性压降的预测结果极为准确。

表1为太极拳锻炼过程中老人下肢左右侧骨骼肌IEMG状况。描述方法采用均值±标准差的方式。分别进行组内左右侧骨骼肌IEMG对比，分析方法为配对样本T检验。结果表明，对照组左右侧胫骨前肌(P=0.045﹤0.05)、股外侧肌(P=0.016﹤0.05)差异显著，实验组股内侧肌(P=0.048﹤0.05)、股外侧肌(P=0.009﹤0.05)、臀大肌(P=0.049﹤0.05)差异显著。

在实验结束后,采取SPSS19.0统计学软件对相关实验资料进行分析和处理,计量资料使用标准差(±s)标示,实行t值检验,计数资料使用百分率(%)标示,实行卡方检验,在P<0.05时组间差异具有统计学意义。

截面收缩工况下,Adam和L-BFGS-B两种优化算法对HLPINN和HPINN的平均计算速度分别如图10(a)和10(b)所示。由图10可见,HLPINN加速效果仍显著依赖于算法的种类。当隐藏层数为6时,Adam算法对HLPINN的计算速度较其对HPINN的计算速度平均提高了204.09%;L-BFGS-B算法对HLPINN的计算速度较其对HPINN的计算速度平均提高了96.31%。当隐藏层数为8时,Adam算法的计算速度平均提高了195.29%;L-BFGS-B算法的计算速度平均提高了79.84%。

=1 000

(

-

)

由图9可见,HLPINN在截面收缩工况下同样可以加速训练过程。当隐藏层数为6时,HLPINN的训练时间比HPINN平均减少了64.29%。当隐藏层数为8时,训练时间平均减少了63.22%。

2.2.2 HLPINN的加速性能研究

2.3 距离函数对HLPINN的影响

为探究施加“硬”边界条件时,距离函数特性对HLPINN求解流动问题的影响,本节对比了几种不同速度边界条件距离函数得到的速度

的相对误差

、训练时间及计算速度。选取的距离函数如下

=10

(

-

)

(19)

截面收缩工况下不同神经网络大小HLPINN和HPINN的训练时间对比如图9所示。物理模型及边界条件、残差点数、优化策略与2.2.1节中的相同。

(20)

=0.1

(

-

)

(21)

=10 000

(

-

)

我的文学作品中不乏苦难，因为这些东西在我的记忆里太深刻了，我不可能忘掉，它们就是我的生活，甚至是我的生活的全部。但是，在给孩子看的作品里面，我始终要给他们亮光，而不是让他们看到一望无际的黑暗。即使写黑暗，我一定要让他们看到亮光，而且还要让他们预感到前面还有更大的亮光。我写苦难没让一个孩子悲观失望、心灰意冷，他们只会在感动中变得昂扬，从今天来看，我的这种尝试是成功的。

(22)

=0.01

(

-

)

在此情境中，教师以学生现实生活中的熟悉的小动物为原型展开图形对称的学习研究，这样的学习对学生来说是有意义的，学生是乐于接受的。

(23)

=min(

,

-|

|)

(24)

(25)

上述距离函数中,函数

～

形式与

相似,只是函数值域被扩大或缩小。

的值域与

相近,但是不如

平滑。

则为一种极端情况,函数在边界上时值为0,反之则为1。利用上述距离函数施加速度边界条件求得的截面扩张和收缩管道内的流体速度

的相对误差

以及相应的训练时间和计算速度如表3所示。在训练过程中,物理模型及边界条件、残差点数、优化策略分别与2.1.1和2.2.1小节中的保持一致,选用的HLPINN大小均为8×100。

分析表3可知,对于截面扩张和收缩两种工况,用

和

施加边界条件求得的误差比

的略大;用

和

施加边界条件求得的误差比

和

的更大,这说明当函数形式相似时,函数的值域对计算误差有很大的影响。

的误差比

的略大,这主要是因为函数

不如

平缓。若用

施加边界条件则无法顺利求解,这主要是因为

不连续。另外,对比

～

的训练时间和计算速度可以发现,距离函数对训练时间和计算速度影响甚微。截面扩张工况下

和截面收缩工况下

、

的训练时间短是由于训练发生病态,损失函数无法继续下降,L-BFGS-B算法自动停止计算导致的。

3 结 论

本文基于HPINN提出了用于求解稳态不可压缩层流流动问题的HLPINN。利用HLPINN和HPINN对截面变化管道内的流动进行了数值模拟,并系统比较了两者的训练时间、计算速度和计算精度,得到如下结论。

(1)HLPINN和HPINN均能精确模拟截面扩张和收缩管道内的流场分布,但是HLPINN的整体计算精度略低于HPINN。对于截面扩张工况,HPINN和HLPINN预测速度

的相对误差

分别低至0.29%和0.53%;对于截面收缩工况,HPINN和HLPINN预测速度

的相对误差

分别低至0.27%和0.41%。

(2)HLPINN相较于HPINN可以加速训练过程,减少训练时间。对于截面扩张和收缩两种工况,HLPINN的训练时间相较于同等大小的HPINN减少超60%。HLPINN可对两种优化算法实现不同程度的加速,对于Adam算法可以提速超过200%,对于L-BFGS-B算法则可提速90%左右。

(3)施加“硬”边界条件的距离函数的形式和值域对计算误差影响很大。研究发现,距离函数必须是连续光滑函数且值域需在合理范围内,但是距离函数对训练时间及计算速度的影响甚微。

除了流体力学(动量传递)问题,HLPINN还有望用于求解热量及质量传递问题。

:

[1] 吴立明,王雷,刘小民,等.仿海鸥翼型动静态气动特性的数值模拟 [J].西安交通大学学报,2020,54(12):88-97.

WU Liming,WANG Lei,LIU Xiaomin,et al.Numerical simulation on the static and dynamic aerodynamic characteristics of bionic seagull airfoil [J].Journal of Xi’an Jiaotong University,2020,54(12):88-97.

[2] 韩馨仪,赵松松,刘斌,等.分体式空调室内气流组织CFD仿真优化 [J].制冷与空调,2021,21(11):41-45.

HAN Xinyi,ZHAO Songsong,LIU Bin,et al.CFD simulation optimization of indoor air distribution in split air conditioner [J].Refrigeration and Air-Conditioning,2021,21(11):41-45.

[3] 樊桦,吴东垠.烟气挡板流动特性的数值模拟 [J].西安交通大学学报,2021,55(2):93-99.

FAN Hua,WU Dongyin.Numerical simulation of the flow characteristics of a flue gas damper [J].Journal of Xi’an Jiaotong University,2021,55(2):93-99.

[4] 胡其会,张鸣远,李景银,等.轴流式血泵水动力特性和生物相容性的数值模拟 [J].西安交通大学学报,2011,45(8):118-122.

HU Qihui,ZHANG Mingyuan,LI Jingyin,et al.Numerical simulation for hydrodynamics and biocompatibility in an axial blood pump [J].Journal of Xi’an Jiaotong University,2011,45(8):118-122.

[5] TRIPATHY R K,BILIONIS I.Deep UQ:learning deep neural network surrogate models for high dimensional uncertainty quantification [J].Journal of Computational Physics,2018,375:565-588.

[6] ZHU Yinhao,ZABARAS N.Bayesian deep convolutional encoder-decoder networks for surrogate modeling and uncertainty quantification [J].Journal of Computational Physics,2018,366:415-447.

[7] JIN Xiaowei,CHENG Peng,CHEN Wenli,et al.Prediction model of velocity field around circular cylinder over various Reynolds numbers by fusion convolutional neural networks based on pressure on the cylinder [J].Physics of Fluids,2018,30(4):047105.

[8] 谢晨月,王建春,万敏平,等.基于人工神经网络的可压缩湍流大涡模拟模型 [J].航空学报,2021,42(9):145-160.

XIE Chenyue,WANG Jianchun,WAN Minping,et al.Artificial neural network model for large-eddy simulation of compressible turbulence [J].Acta Aeronautica et Astronautica Sinica,2021,42(9):145-160.

[9] KIM J,LEE C.Prediction of turbulent heat transfer using convolutional neural networks [J].Journal of Fluid Mechanics,2020,882:A18.

[10] RAISSI M,PERDIKARIS P,KARNIADAKIS G E.Physics informed deep learning:part I data-driven solutions of nonlinear partial differential equations [EB/OL].[2022-03-13].https:∥doi.org/10.48550/arXiv.1711.10561.

[11] RAISSI M,PERDIKARIS P,KARNIADAKIS G E.Physics-informed neural networks:a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations [J].Journal of Computational Physics,2019,378:686-707.

[12] JIN Xiaowei,CAI Shengze,LI Hui,et al.NSFnets (Navier-Stokes flow nets):physics-informed neural networks for the incompressible Navier-Stokes equations [J].Journal of Computational Physics,2021,426:109951.

[13] 侯龙锋,朱兵,张伟.基于PINN神经网络算法的低雷诺数下槽道流模拟方法 [C]∥第三十一届全国水动力学研讨会论文集:上册.北京:法律出版社,2020:1037-1044.

[14] CAI Shengze,WANG Zhicheng,WANG Sifan,et al.Physics-informed neural networks for heat transfer problems [J].Journal of Heat Transfer,2021,143(6):060801.

[15] CAI Shengze,WANG Zhicheng,FUEST F,et al.Flow over an espresso cup:inferring 3-D velocity and pressure fields from tomographic background oriented Schlieren via physics-informed neural networks [J].Journal of Fluid Mechanics,2021,915:A102.

[16] SUN Luning,GAO Han,PAN Shaowu,et al.Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data [J].Computer Methods in Applied Mechanics and Engineering,2020,361:112732.

[17] BERG J,NYSTRÖM K.A unified deep artificial neural network approach to partial differential equations in complex geometries [J].Neurocomputing,2018,317:28-41.

[18] 陆至彬,瞿景辉,刘桦,等.基于物理信息神经网络的传热过程物理场代理模型的构建 [J].化工学报,2021,72(3):1496-1503.

LU Zhibin,QU Jinghui,LIU Hua,et al.Surrogate modeling for physical fields of heat transfer processes based on physics-informed neural network [J].CIESC Journal,2021,72(3):1496-1503.

[19] ZHU Qiming,LIU Zeliang,YAN Jinhui.Machine learning for metal additive manufacturing:predicting temperature and melt pool fluid dynamics using physics-informed neural networks [J].Computational Mechanics,2021,67(2):619-635.

[20] RAO Chengping,SUN Hao,LIU Yang.Physics-informed deep learning for incompressible laminar flows [J].Theoretical and Applied Mechanics Letters,2020,10(3):207-212.

[21] LAUBSCHER R,ROUSSEAU P.Application of a mixed variable physics-informed neural network to solve the incompressible steady-state and transient mass,momentum,and energy conservation equations for flow over in-line heated tubes [J].Applied Soft Computing,2022,114:108050.

[22] BAYDIN A G,PEARLMUTTER B A,RADUL A A,et al.Automatic differentiation in machine learning:a survey [J].Journal of Machine Learning Research,2018,18(153):1-43.

[23] GLOROT X,BENGIO Y.Understanding the difficulty of training deep feedforward neural networks [C]∥Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics.Chia Laguna Resort,Sardinia,Italy:PMLR,2010:249-256.

[24] KINGMA D P,BA J.Adam:a method for stochastic optimization [EB/OL].[2022-03-13].https:∥doi.org/10.48550/arXiv.1412.6980.