圆锥角对功能梯度壳非线性振动响应的影响*

张宇航， 刘文光， 刘 超， 吕志鹏

（南昌航空大学 航空制造工程学院，南昌 330063）

引 言

功能梯度材料(functionally graded materials，FGMs)是一种新型复合材料，通常由金属和陶瓷组成，并按不同的体积分布函数沿厚度方向呈梯度变化.这种材料同时具有金属和陶瓷的优点，能够有效降低结构的应力集中，在航空航天领域有着广泛的应用前景.而在飞行器飞行过程中，振动载荷是不可避免的，对飞行器结构的安全可靠性影响巨大.因此，为了推动FGMs在飞行器结构设计上的应用，深入了解FGMs结构的振动特性具有重要意义.

近年来，研究者们围绕FGMs结构的动力学分析做了大量的工作.基于Love薄壳理论，Loy等求解了采用幂律分布函数的FGMs圆柱壳的模态频率，分析了不同分布函数指数、轴向波数、环向波数对结构模态频率的影响[1].基于小振幅和谐振假设条件，李世荣等推导了表面粘贴压电层FGMs弹性梁的热-力-电耦合动力学方程，分析了不同载荷下弹性梁的屈曲与自由振动响应[2].通过一阶剪切变形理论，徐坤等建立了四边简支FGMs板的运动微分方程，探究了体积分布函数对板自由振动和受迫振动的影响[3].除了经典边界条件，研究者对弹簧模拟FGMs结构的任意边界条件开展了研究.采用改进的Fourier级数构造位移容许函数，李文达等分析了旋转FGMs圆柱壳的行波特性，研究了圆柱壳几何参数、旋转速度对行波频率的影响[4].采用Rayleigh-Ritz法，田宏业等求解了FGMs圆锥板的模态频率[5].结合反拉氏变换与微分求积法，Liang等研究了不同边界、热环境、弹性支撑和几何参数对FGMs圆柱壳振动的影响[6].

由于大变形条件下，FGMs结构不可避免地产生非线性振动，使得结构的分岔、非线性模态得到了研究者们的广泛关注.杜长城等围绕FGMs圆柱壳的分岔行为，讨论了调谐参数对分岔的影响[7].考虑到FGMs结构服役过程中，不可避免地受到外部载荷激励作用，许多研究者讨论了外载荷对结构非线性行为的影响.基于Donnell壳理论，Liu等研究了弹性支撑下含孔隙FGMs层合圆柱壳受点载荷作用下的非线性振动特性，揭示了壳的多重内共振行为[8].针对不同的FGMs幂律分布函数，Hamid等分析了横向激励下FGMs圆锥壳的非线性主共振行为[9].利用sigmoid材料分布函数，Singh等研究了几何尺寸、材料组分对横向载荷下陶瓷金属FGMs板非线性振动的影响，分析了FGMs板进入混沌运动的路径[10].考虑气动载荷和面内载荷的耦合作用，Yang等推导了FGMs圆锥壳的非线性运动方程，求解了圆锥壳的主共振响应和次谐波响应，讨论了圆锥壳振动的混沌行为[11].随着压电结构在工程中的广泛应用，陆续有研究者采用压电结构作为控制器对FGMs结构进行主动控制.以外层压电层为作动层，Nguyen分析了压电功能梯度层合圆柱壳外加电场致非线性振动时域响应[12].Moghaddam等分析了在谐波激励下施加电压对不同材料分布函数压电功能梯度壳非线性响应的影响[13].

工程实践中，航空航天领域的很多板壳结构在一定条件下可以简化为圆锥壳模型，而且这些锥壳结构通常要承受振动冲击和高温高压等载荷的作用，致使圆锥壳结构产生非线性振动.为了推进FGMs在航空航天结构设计中的应用，本文以FGMs圆锥壳为对象，考虑von Kármán几何非线性推导了FGMs圆锥壳的非线性动力学方程，讨论了不同材料分布以及陶瓷体积分数指数对FGMs圆锥壳非线性振动的影响，研究了在不同激励幅值下锥角对FGMs圆锥壳运动形式的影响.

1 FGMs圆锥壳模型

以图1所示的圆锥壳模型为对象，假设锥角为2α0，壳厚为h，母线长为L，圆锥小端的中面半径为R1，大端的中面半径为R2.α0=0°时，圆锥壳模型可以转化为圆柱壳；α0=90°时，圆锥壳模型则转化为圆环板.以圆锥壳的中面为基准，建立图1所示的柱坐标系Oxθz.坐标系中，x表示圆锥壳的母线方向，θ表示圆锥壳的圆周方向，z表示圆锥壳的厚度方向.因此，沿x轴上任一点的半径R可由x表示：

假设FGMs圆锥壳受外部横向载荷F作用：

式中，F'表示振幅，Ω表示载荷激励频率.

假设FGMs圆锥壳的外表面为纯陶瓷、内表面为纯金属，而且材料沿厚度方向的分布用Voigt模型来描述，则其物理属性表达式为

式中，Pc，Pm分别表示陶瓷和金属的材料属性(如弹性模量E、密度ρ、Poisson比ν)，Vc，Vm分别表示陶瓷和金属的体积分数.

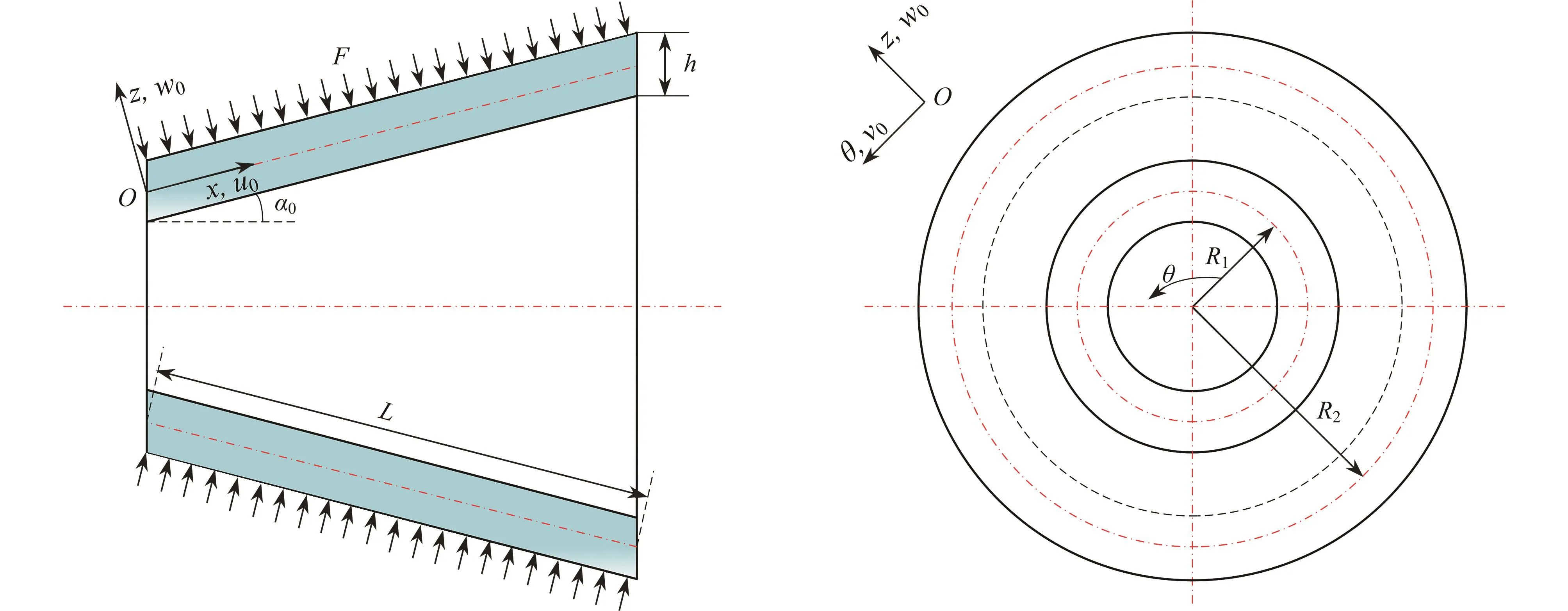
图 1 几何模型Fig. 1 The geometric model

2 非线性运动方程

由一阶剪切变形理论，圆锥壳上任意一点的位移沿x，θ，z方向的位移分量可由中面位移表示：

式中，t表示时间；u，v，w分别表示圆锥壳上沿x，θ，z轴任意一点的位移；u0，v0，w0表示圆锥壳中面上的位移；φx，φθ分别表示圆锥壳沿轴x，θ方向的转角.

考虑von Kármán非线性，圆锥壳的应变与位移的关系表示为

其中

式中，εx，εθ表示任意一点沿x，θ方向的正应变，γxθ表示xOθ平面内的切应变，γxz表示xOz平面内的切应变，γθz表示θOz平面内的切应变；表示中面曲面应变分量，κx，κθ，κxθ表示中面曲面曲率.

FGMs圆锥壳的本构关系可表示为

式中，σx，σθ是任意一点沿x，θ方向的正应力，τxθ是xOθ平面内的切应力，τxz是xOz平面内的切应力，τθz是θOz平面内的切应力；刚度元素Qij(i,j=1, 2, ···，6)可以表示为

FGMs圆锥壳的应变能可以表示为

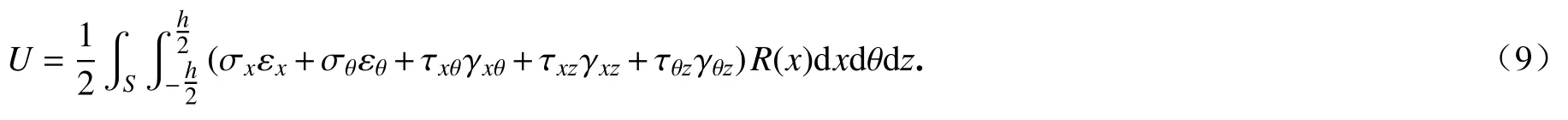
FGMs圆锥壳的动能可以表示为

横向外载荷所做的功可以表示为

根据Hamilton原理，FGMs圆锥壳的运动方程可以表示为

式中，Nx，Nθ，Nxθ表示内力，Mx，Mθ表示弯矩，Mxθ表示扭矩，I1，I2，I3为惯性矩，具体表达式为

式中，ε0表示应变向量，N表示内力矩阵，M表示弯矩矩阵，A，B，D表示刚度矩阵，表达式分别为

刚度元素Aij，Bij，Dij(i,j=1, 2, ···，6)的具体表达式为

式中，Qxz,Qθz表示剪切刚度，κc表示剪切修正系数[14]，取5/6.

3 简支FGMs圆锥壳的非线性振动分析

假设FGMs圆锥壳两端简支，满足边界条件的圆锥壳位移函数可以假设为

式中，umn(t),vmn(t),wmn(t),pmn(t),qmn(t)表示关于时间t的变量，n，m分别为环向波数和轴向波数.

假设外部横向载荷可以定义为三角函数形式：

式中，f表示外部横向载荷幅值.

为简化分析，本文只讨论FGMs圆锥壳的横向振动[15].将式(20)和(21)代入方程(12)，采用Galerkin法可将FGMs圆锥壳振动模型简化为非线性单自由度振动系统：

式中，M为广义质量，C为比例阻尼，K1为线性刚度系数，K2为非线性刚度系数.

定义以下无量纲量：

将式(23)代入方程(22)可得到

其中

式中，ω0为FGMs圆锥壳的线性频率，表达式为

假设方程(24)解的Fourier形式为

取一阶截断，可得

将式(27)和(28)代入方程(24)，通过忽略高阶谐波项，同时考虑圆锥壳的稳态响应，比较cos(ωrτ)和sin(ωrτ)项的系数，可得

令

式中，χ表示无量纲振动幅值.

方程(29)可进一步简化为

4 结果分析与讨论

4.1 模型验证

为验证FGMs圆锥壳动力学模型的可靠性，分别将模型退化为FGMs圆柱壳和纯金属圆锥壳.表1所示是不锈钢和Ni的材料参数.通过式(26)计算线性模态频率，并与文献[1]结果进行对比，结果如表2所示，其中f=ω0/(2π).表3反映了纯金属圆锥壳模态频率随环向波数的变化情况.结果表明，本文模型得到的计算结果和文献[16-17]结果比较吻合.

表 1 FGMs圆柱壳的材料参数Table 1 Material parameters of FGMs cylindrical shells

表 2 FGMs圆柱壳频率对比(R1=1, R1/h=500, L/R=20, m=1)Table 2 Comparison of frequencies of FGMs cylindrical shells (R1=1, R1/h=500, L/R=20, m=1)

表 3 纯金属圆锥壳频率对比(R2=1, R2/h=100, Lsin(γ0)/R2=0.25, α0=30°, m=1)Table 3 Comparison of frequencies of pure metal conical shells (R2=1, R2/h=100, Lsin(γ0)/R2=0.25, α0=30°, m=1)

4.2 幅频响应分析

假设FGMs圆锥壳的材料组分为Si3N4以及SUS304.数值分析时，两种材料的性能分别取：弹性模量Ec=322.27 GPa，Em=207.787 7 GPa，密度ρc=2 470 kg/m3，ρm=8 166 kg/m3，Poisson比νc=0.3，νm=0.317 7.圆锥壳的几何参数分别为：L/R1=4，R1/h=20，h=0.01 m，α0=15°.圆锥壳施加的外部载荷幅值取= 10，频率比ωr=1，阻

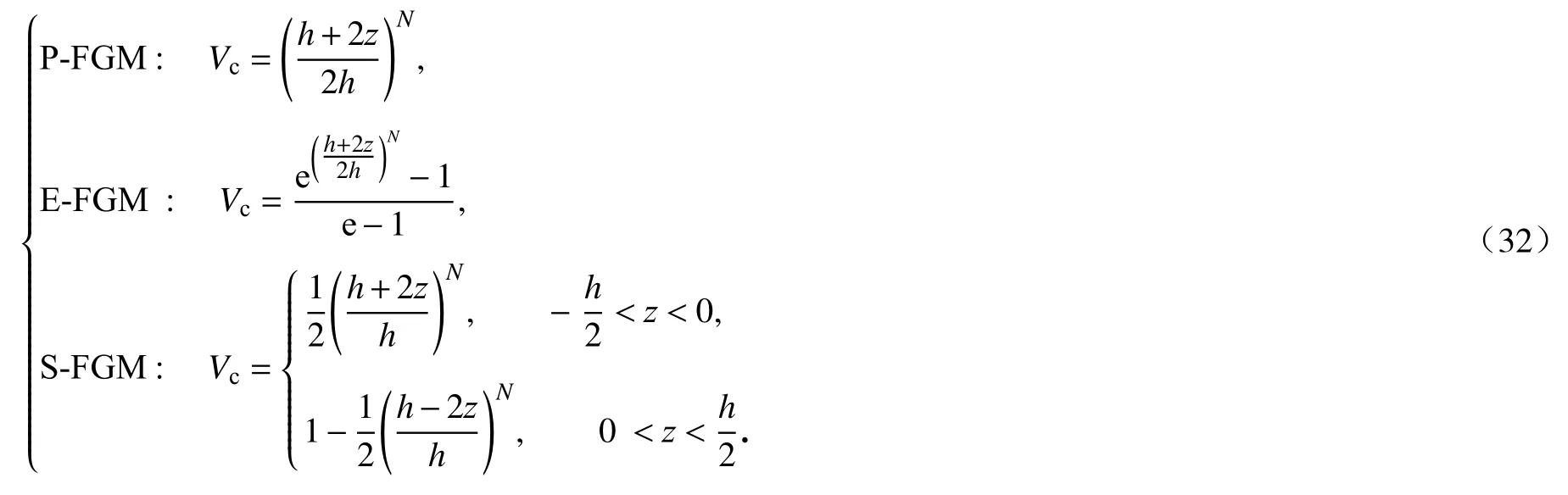
图2所示是不同陶瓷体积分数随陶瓷体积分数指数N的变化规律.图3探究了不同材料分布函数对FGMs圆锥壳非线性振动的影响.结果表明，FGMs圆锥壳的材料分布沿厚度方向服从幂律分布和指数分布模型时，随着陶瓷体积分数指数的增大，FGMs圆锥壳的幅值增大，这是因为陶瓷含量减少，圆锥壳的刚度下降，FGMs圆锥壳的渐硬弹簧特性减弱.反之，采用sigmoid分布模型，随着陶瓷体积分数指数的增大，渐硬弹簧特性增强.

图 2 陶瓷体积分数指数沿厚度方向的变化Fig. 2 Variations of ceramic volume fraction exponents along the thickness direction

4.3 分岔混沌分析

图3结果表明，陶瓷材料分数指数对FGMs圆锥壳的非线性振动影响不明显.考虑到幂律分布在FGMs结构加工过程中更易实现，下面基于幂律分布函数进一步揭示FGMs圆锥壳丰富复杂的非线性现象.计算时，取分数指数N=1.图4、图5讨论了圆锥锥度以及载荷幅值对结构非线性特性的影响.

图 3 陶瓷体积分数指数对FGMs圆锥壳幅频响应特性曲线的影响Fig. 3 Effects of ceramic volume fraction exponents on nonlinear amplitude frequency responses of FGMs conical shells

图 4 不同锥度下FGMs圆锥壳随激励幅值变化的分岔图Fig. 4 The bifurcation diagrams of FGMs conical shells for different excitation amplitudes under different cone angles

图4表明，当α0=15°时，圆锥壳存在多个混沌运动区域，从周期运动到多周期运动再到混沌运动；当激励载荷达到52 ~ 54，60 ~ 68，74 ~ 80以及84 ~ 88时，非线性进入混沌运动.当α0增大到30°时，圆锥壳的混沌运动只存在一个载荷幅值区间，混沌产生所需要的激励幅值需要达到95 ~ 98.在载荷小于该值范围时，圆锥壳只表现为周期以及多周期运动.当α0继续增加到60°时，圆锥壳在30 ~ 100的激励幅值区间内不再出现混沌现象.换句话说，增大圆锥壳的锥度，结构的混沌现象将会被延后，甚至消失.

考虑α0=15°时，FGMs圆锥壳的分岔现象更为丰富.以α0=15°为例，图5给出了激励幅值取45，65，72时，FGMs圆锥壳相应的时间历程、相图曲线和Poincaré截面图，观察到圆锥壳分别表示为周期、混沌以及多周期运动.通过增大圆锥壳的锥度可以有效地延缓运动不稳定性的发生.

图 5 不同激励幅值下FGMs圆锥壳时间历程曲线、速度位移相图以及Poincaré截面图(α0=15°)Fig. 5 The time history diagrams, phase plots and Poincaré maps of FGMs conical shells under different excitation amplitudes (α0=15°)

5 结 论

本文采用Hamilton原理以及Galerkin法推导了FGMs圆锥壳的运动方程，利用谐波平衡法求解了FGMs圆锥壳的非线性振动幅频响应，讨论了不同材料分布函数下陶瓷体积分数指数对FGMs圆锥壳非线性特性的影响，分析了FGMs圆锥壳的分岔现象，讨论了圆锥角和外部载荷幅值对FGMs圆锥壳运动状态的影响.主要结论如下：

1) 材料分布函数对FGMs圆锥壳的非线性特性影响不明显，FGMs圆锥壳的振动特性都呈现渐硬弹簧非线性特性.

2) 外部激励幅值的变化导致FGMs圆锥壳产生丰富的非线性现象，结构出现周期、多周期、混沌运动.

3) 锥角较小时，FGMs圆锥壳会出现多个混沌区域，圆锥壳的运动具有不可预测性；锥角增大，混沌区域集中发生在大载荷幅值95 ~ 100的范围内，圆锥壳的混沌运动产生条件更为困难.