Boussinesq方程温和解的全局适定性*

周艳平， 王 珣， 别群益

（三峡大学 理学院，湖北 宜昌 443002）

引 言

Boussinesq方程是Navier-Stokes方程与热力学方程之间耦合的零阶近似，是描述在重力作用下的流体动力学方程，并且已广泛地应用于大气科学与海洋环流的研究中，如气旋、飓风和海啸等突发的自然灾害[1-5].在过去几十年中，数学家已经对大气、海洋以及大气和海洋耦合的原始方程进行了广泛的研究，尤其是原始方程组的适定性和自身的稳定性等问题[6-7]. Boussinesq方程具体的数学表达式如下[5]：

这里θ和 u = (u1,u2,···,uN)分别表示温度和流体的速度，p 表示压力，常向量 β∈RN与流体的热展开系数成正比，函数 u0及 θ0表示给定的初始值.系统(1)具有尺度不变性，即对任意 λ＞0， (uλ,θλ) 仍然是系统的解，其中

系统(1)在各种不同空间中解的存在唯一性结果可参考文献[8-14].文献[15]研究了其解的大时间行为.在尺度不变意义下，文献[16]证明了系统(1)在拟测度空间上温和解的自相似性.对于Keller-Segel方程与Navier-Stokes方程的耦合系统，文献[17]在关于时间加权的Lebesgue空间上，利用隐函数定理证明了其温和解的全局存在唯一性.另外，文献[18-19]分别得到了磁流体方程及向列型液晶方程在尺度不变空间下温和解的全局适定性.

受上述文献的启发，本文的主要目的是研究当初始值 (u0,θ0)在尺度不变的弱Lebesgue空间中具有小性时，系统(1)的温和解在 (t,x)∈R+×RN(N≥3)上的全局适定性.

下面引入弱-Lp空间，其范数定义为

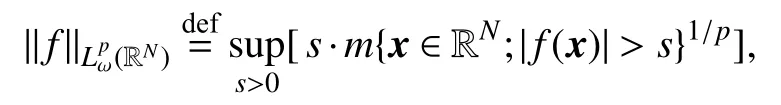
其中m表 示 Lebesgue测 度.在后文中，有时会将 Lp(RN)和分别缩写为Lp和.

定义1 设空间维数 N≥3，初始值 (u0,θ0)满足

对 t∈(0,∞)成立，则称可测函数 (u,θ)在 (t,x)∈(0,∞)×RN上是系统(1) 的一个温和解.这里 etΔ表示如下定义的热半群：

这里 Rj≡∂/∂xj(-Δ)-1/2表示 Riesz算 子.

本文的主要结论如下.

定理1(存在唯一性) 假设空间维数 N≥3.设指标 p,q 满足如下三个关系式之一：

那么存在一个常数 δ=δ(N,p,q)，当初始值 (u0,θ0)满足

其中记号Cω([0,∞);X)表示在 [0,∞)上取值于Banach空间X 上的有界弱-∗连续函数的集合(详见文献[20]).

若式(7)、(8)中对应空间范数充分小，则温和解 (u,θ)是唯一的.另外，当 t→∞时， (u,θ)具有如下的渐近性：

1 关 键 引 理

首先引入如下定义的两个函数空间X和Y：

其范数定义为

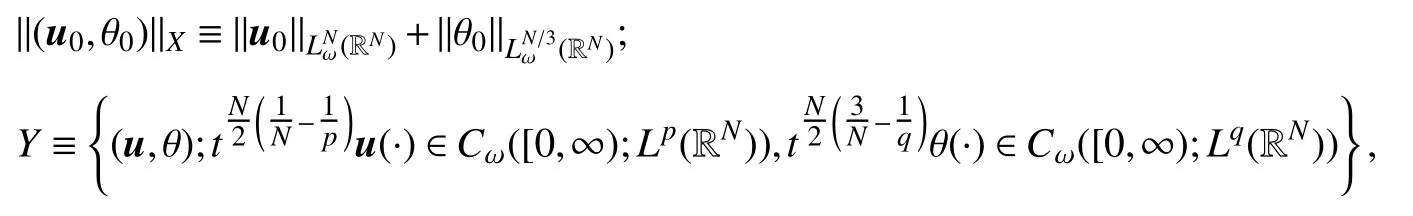
其范数定义为

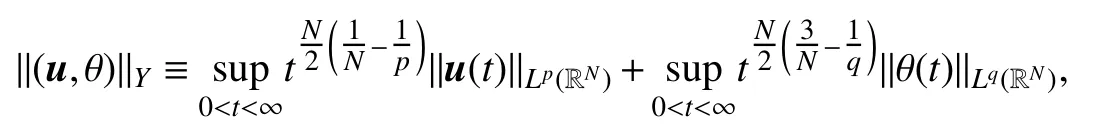
其中当 N = 3时，在X中用 θ0∈L1(R3)代替赋予上述范数后X和Y均是 Banach 空间.

对(u0,θ0)∈X 以及 (u,θ)∈Y ，定义映射

这里

那么有下面的关键引理.

引理1假定空间维数N≥3.设指标p,q满足如下三个关系之一：

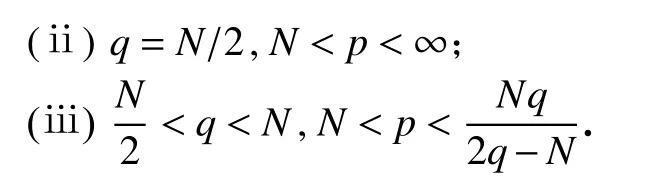
则① 由式(14)定义的映射F是一个从X×Y到Y的连续映射； ② 对每一个初值 (u0,θ0)∈X ，映射 F(u0,θ0,·,·)是从Y到Y的C1类映射.

证明首先证明

这里C =C(N,p,q)，记号h(s,t)(s＞0,t＞0)表示beta 函数：

需要说明的是，在式(17)的第一个不等式中, 利用了投影算子P在Lp(1＜p＜∞)上的有界性.

由于1/2-N/(2p)＞0，类似地，对所有 t＞0，有

上式中当 N = 3时，用 L1(R3)代替由于以及，则

对所有 t＞0成立.

基于式(19)和(22)，得

且存在C =C(N,p,q)，使得

这就意味着F是从X×Y到Y的连续映射.

下面证明映射F属于C1类.对任一 (u,θ)∈Y，在Y上定义线性映射

其中

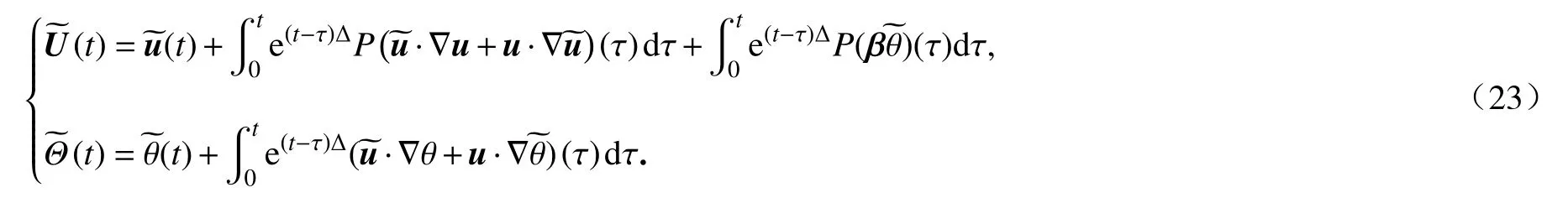
下面将证明对每个 {u0,θ0}∈X，线性算子 L{u,θ}是 F(u0,θ0,u,θ)在 (u,θ)∈Y 处的 Fre´chet导数.

定义{U,f}为

则有

由式(18)可知，对所有t＞0，满足

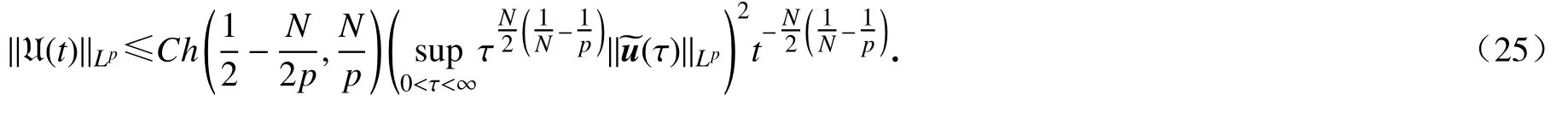
同样由式(21)可知

对所有 t＞0成立.结合式(25)、(26)，对任意 (u0,θ0)∈X 及任意 (u,θ)∈Y ，有

这蕴含F在点(u0,θ0,u,θ)∈X×Y 处，沿着方向 (u,θ)的 Frchet 导数是引理1证毕.

2 主要结果的证明

定理1的证明 首先证明线性算子 L{u,θ}在 (u,θ) = (0,0)点处是双射.由式(23) 可知，对，线性算子可表示为

利用隐函数定理可知，存在常数δ(N,p,q)＞0及如下定义的C1类映射g：

使得对所有(u0,θ0)∈Xδ，有

因此，由条件(5)、(6)，泛函 g(u0,θ0)给出了系统(2)满足式(7)、(8)的唯一解.

若系统(2) 满足式(7)、(8)的解 (u,θ)在Y上的范数很小时，根据映射h是 从 Xδ到 Yδ的C1类映射, 可以得出解(u,θ)的唯一性.另外式(9)、(10)的渐近性可分别从估计式(17)、(18)及(21)得到.至此定理1证毕.

定理2的证明 由于映射 h : Xδ→Yδ是连续的，所以当初始值满足式(12)时，可以得到式(13)的稳定性估计.至此我们完成了定理2的证明.

3 结 论

Boussinesq方程作为描述许多地球物理现象的模型，是Navier-Stokes方程与热力学方程之间耦合的零阶近似.本文利用隐函数定理，得到了高维具黏性的Boussinesq系统温和解的全局适定性，即解的存在唯一性及稳定性，其中，系统的初值位于尺度不变意义下的弱Lebesgue空间且具有小性.