非线性弹性杆波动方程的显式精确解*
郭 鹏, 唐荣安, 孙小伟, 洪学仁, 石玉仁
(1. 兰州交通大学 材料科学与工程学院,兰州 730070;2. 兰州交通大学 数理学院,兰州 730070;3. 兰州交通大学 铁道车辆热工教育部重点实验室,兰州 730070;4. 西北师范大学 物理与电子工程学院,兰州 730070)
引 言
杆是重要的工程应用元件,杆件中的波动特别是非线性波的研究日益引起科研人员的关注,现已成为工程领域的一个研究热点[1-6].在文献[1]中,张善元和庄蔚建立了计入横向惯性效应任意形状截面的非线性弹性杆波动方程,其形式为

其中,s 为杆截面积,Jρ为杆截面的极惯性矩,= E/ρ为线弹性纵波波速平方,E为弹性模量,ρ为杆的密度,ν为Poisson比,an和n均 为材料常数.取材料常数 n = 2,通过变换将方程变换为KdV方程并用逆散射方法获得了KdV方程的孤波解,证明了在材料常数 n = 2时,非线性弹性杆中存在孤波.很多学者对非线性弹性杆中的孤波问题进行了研究.在文献[7]中,胡伟鹏等取材料常数 n = 2,用多辛方法对方程(1)进行了数值模拟,讨论了非线性效应和几何弥散效应对孤波传播的影响.在文献[8]中,Duan和Zhao取材料常数 n = 3,用约化摄动方法将方程(1)变换为非线性Schrödinger方程,得到了方程的包络孤波解.在文献[9]中,郭鹏等取材料常数n≥2,用约化摄动方法将方程(1)变换为变形KdV方程.在文献[10]中,吕克璞等取材料常数 n≥2,用约化摄动方法将方程(1)变换为非线性Schrödinger方程.以上研究证明了在材料常数 n≥2时,非线性弹性杆中存在孤波和包络孤波.但是需要注意的是,用约化摄动方法获得的解还是方程的近似解.在文献[11]中,Kabir取材料常数 n = 2,用修正的Kudryashov方法、(G′/G)展开法和exp函数法获得了方程(1)的精确解.在文献[12]中,Çelik等取材料常数 n = 2,用Lie群分析方法和F-展开法获得了方程(1)的精确解.在文献[13-14]中,Li等用平面动力系统方法研究了材料常数 n = 2, 3, 5以及大于5的奇数情况下的精确解.
非线性弹性杆波动方程的求解尽管已经有了上述研究工作,但是对于方程(1)中材料常数n取不同数值时(包括分数),求解(特别是精确解)仍然是很困难的.值得注意的是,对于非线性方程的求解,经过相关学者近几十年来的努力,目前已经发展出了很多精确求解的方法[15-36].在这些求解方法中,sine-cosine方法是一种较为简便的方法.这种方法的思路是将方程的解拟设为正弦或余弦函数形式,然后将正弦或余弦函数形式的解代入原方程,用待定系数法确定相应的常数,从而获得方程的精确解.本文应用sine-cosine方法[29-33]对非线性弹性杆波动方程进行了求解,得到了该方程的一些新的周期波解和孤波解.对材料常数n不等于1(包括材料常数n为不等于1的分数)的非线性弹性杆中孤波的存在性给出了理论证明.
1 非线性弹性杆波动方程的求解
对方程(1)引入如下变换:

其中k ,c 为待定常数.将方程(2)代入方程(1)可得

将方程(3)对ξ积分一次,并取积分常数为零可得

令

则方程(4)的形式可简化为
其中

假设方程(6)的解为

将方程(8)代入方程(6)可得

为使方程(9)有非零解,需要平衡其中第二和第三项正弦函数的指数,使得


令方程(11)中正弦函数前的系数为零,可得

由方程(12)解得

将方程(13)及α,β代入方程(8),可得

同理,若假设方程(6)的解为

将方程(16)代入方程(6),得到的解为


可将方程(14)、(15)、(17)、(18)化为
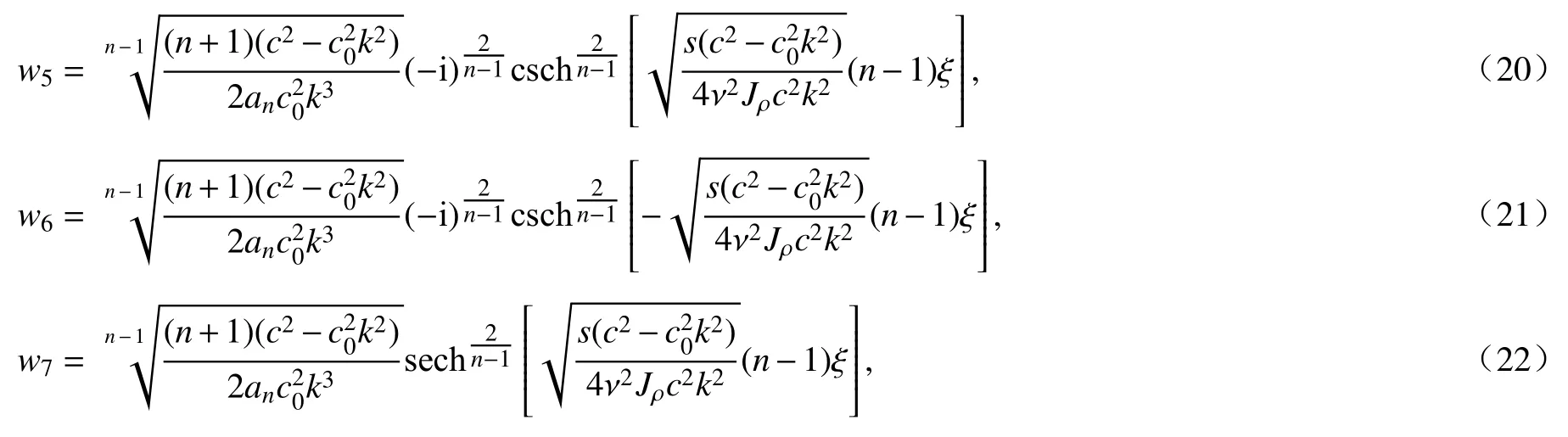

根据方程(5),将方程(14)、(15)、(17)、(18)对ξ积分一次,可得

方程(24)~(27)即为非线性弹性杆波动方程的三角函数周期波解.
同理,将方程(20)~(23)对ξ积分一次,可得

方程(28)~(31)即为非线性弹性杆波动方程的孤波解.
有了以上精确解的表达式,只要确定了材料常数n,即可通过积分获得非线性弹性杆波动方程的精确解.例如,当材料常数时,由方程(24)~(31)可得


其中,C为 积分常数.
当材料常数 n = 3时,由方程(24)~(31)可得


由材料常数n取 其他不同的数值,我们还可以获得更多新的精确解,此处不再一一列出.
2 结果与讨论
应用sine-cosine方法对非线性弹性杆波动方程进行了求解,得到了一些新的周期波解和孤波解.根据获得的精确解,还可以很方便地绘制精确解的图像.例如图1绘制了当 c = 1.5, k = 1, an= 0.7, c0= 100, ν= 0.4,Jρ= 0.3, s = 3.5,C = 0时,方程(34)的三角函数周期波解;图2绘制了当 c = 100, k = 0.5, an= 0.7, c0= 30, ν= 0.2,Jρ= 0.1, s = 10, C = 0时,方程(38)的孤波解.所获得的非线性弹性杆波动方程的新精确解(特别是孤波解)对助于该问题的进一步研究.从求解非线性弹性杆波动方程的过程可以看出,sine-cosine方法是一种简便、有效的方法.在文献[32-33]中,采用sine-cosine方法同样简便地获得了KdV方程、修正KdV方程、广义KdV方程、Boussinesq方程、RLW方程、BBM方程、Phi-4方程、修正Degasperis-Procesi方程、修正Camassa-Holm方程的精确解.这种方法还可用于其他非线性方程或方程组的求解.
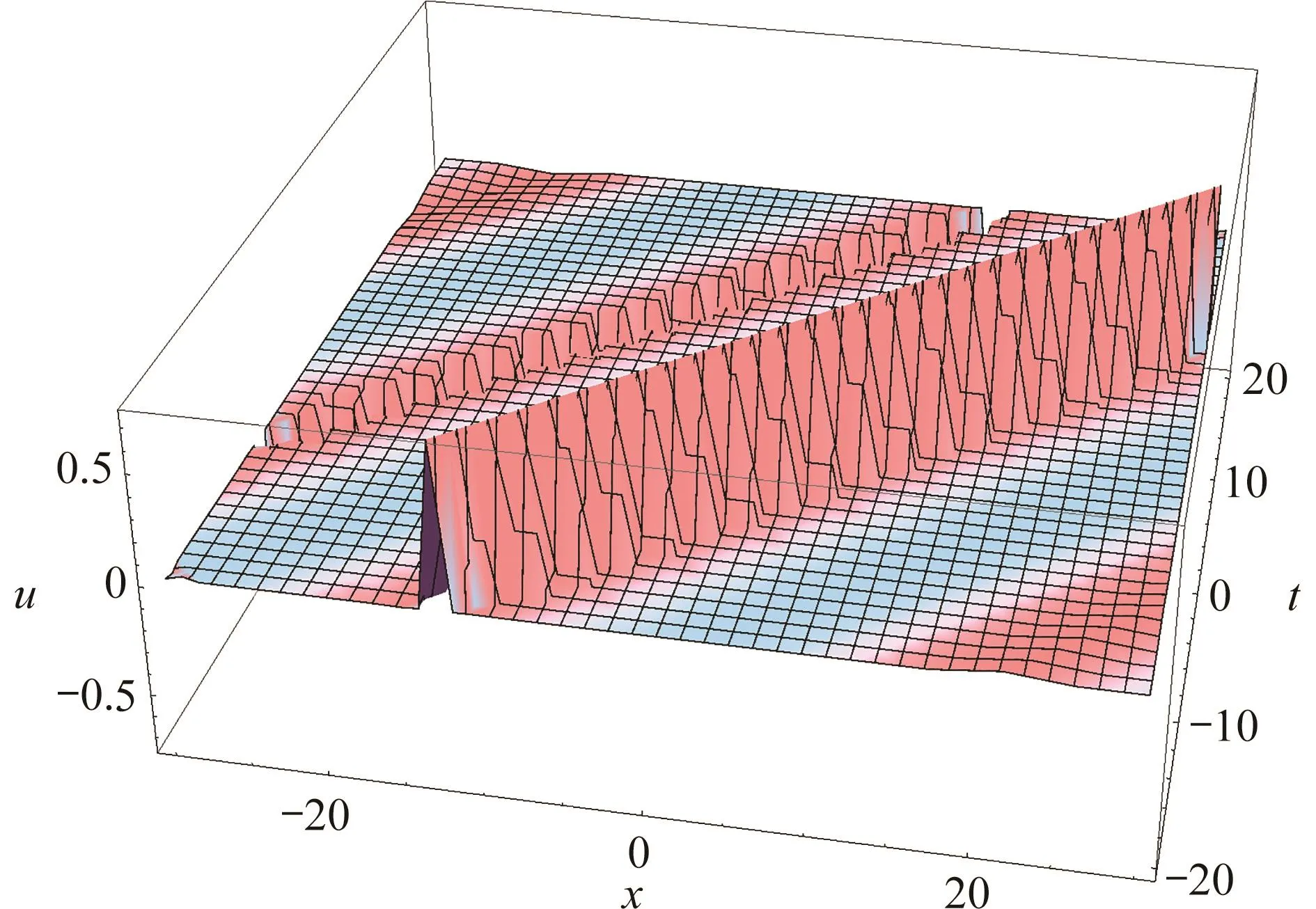
图 1 方程(34)解的图像Fig. 1 Graphical representation of solution (34)

图 2 方程(38)解的图像Fig. 2 Graphical representation of solution (38)
3 结 束 语
非线性弹性杆波动方程的求解尽管已经有了相关参考文献及本文所开展的上述研究工作,但是对于方程(1)中材料常数取不同数值时(包括分数)的求解仍然是很困难的.继续研究新的求解方法与获得同类型方程更丰富的解,值得研究工作者们进行更深入的钻研与探索.

