A theoretical investigation of glide dislocations in BN/AlN heterojunctions
Shujun Zhang(张淑君)
Department of Physics,Chongqing Three Gorges University,Wanzhou 404100,China
Glide dislocations with periodic pentagon-heptagon pairs are investigated within the theory of one-dimensional misfit dislocations in the framework of an improved Peierls–Nabarro (P–N) equation in which the lattice discreteness is fully considered. We find an approximate solution to handle misfit dislocations,where the second-order derivative appears in the improved P–N equation. This result is practical for periodic glide dislocations with narrow width,and those in the BN/AlN heterojunction are studied. The structure of the misfit dislocations and adhesion work are obtained explicitly and verified by first-principles calculations. Compared with shuffle dislocations, the compression force in the tangential direction of glide dislocations has a greater impact on the normal direction, and the contributions of the normal displacement to the interfacial energy cannot simply be ignored.
Keywords: interfacial misfit dislocation,misfit dislocation energy
1. Introduction
It is well known that a large number of dislocations are often induced under mismatch strain field in crystal composites due to inevitable mismatch between interfaces of two different types of crystals. Frank and van der Merwe[1]proposed the concept of misfit dislocations when studying monolayers on crystalline substrates, which is referred to as the Frenkel–Kontorova model. Historically, the well-known Peierls–Nabarro(P–N)model[2,3]was the first to describe dislocation cores at the atomic scale. Later, van der Merwe[4,5]extended the P–N theory to investigate the interface between two semi-infinite crystals and introduced various elastic parameters and lattice constants. Dundurs and Hetenyi[6]produced an explicit expression for the stress function in the limiting case of concentrated forces acting perpendicular to the interface of two semi-infinite crystals based on the Airy stress function in problems from the theory of elasticity,which may be found in the review by Muskhelishvili.[7]Dundurs then obtained the Airy stress function with dislocations at the interface of two different lattices through an analogy between concentrated forces and edge dislocations.[8]Based on Dundur’s results and within the framework of linear elastostatics, the periodic interfacial misfit dislocation equation was discovered by Yaoet al.[9,10]Since then,the appearance of second-order derivative terms has further developed the P–N theory for misfit dislocations,[11]which has been applied to reveal the associated core structure.[11,12]
Currently, as interface structures and the resultant properties of interfaces play a vital role in determining the material strength, many investigations focused on the influences of misfit dislocations toward the resulting mechanical properties. Although the atomic configuration of interfaces can be determined from the relationship between the mass center displacement and the relative displacement,which has been verified in a two-dimensional(2D)AlN/BN heterojunctions,there are some discrepancies between the theoretical and numerical results for the displacement of shuffle dislocations along interfacial spacings. There are two kinds of interfacial misfit dislocations in 2D honeycomb structures: Glide dislocations with a periodic array of pentagon-heptagon rings,and shuffle dislocations with a periodic array of hexagon-octagon rings. Many studies on the structural stability of two kinds of dislocation,e.g.,reviewed by Zhanget al.[13]and Yaoet al.,[14]have been studied for graphene. This indicates that a similar situation also exists at the interface of BN/AlN heterojunctions, which involves the structural stability of 1D direction misfits. The adhesion work is generally used to determine the most likely form of dislocations. However,to the author’s knowledge,the structure of glide dislocations for honeycomb structures in 2D heterojunctions has not been addressed theoretically.
Recently, we extended the original P–N model by considering interface effects and applied it to the investigation of misfit dislocations where the lattice parameters differed in one direction only. In the present work, we focus on glide dislocations with periodic pentagon-heptagon pairs in AlN/BN heterojunction interfaces.The narrow interfacial spacing at interfaces where glide dislocations are located indicates that the influence of the interfacial spacing variations caused by misfit dislocations at normal interfaces needs to be considered.
2. The γ-surface of glide dislocations
Dislocation core structures and mobilities are usually studied using the classic P–N model.[15–20]However,as arrays of atoms at the interface have varying lattice parameters, van der Merwe[5]proposed a reference lattice to represent the effective interactions between two dissimilar semi-infinite crystals. As illustrated in Fig.1(a),we consider a 2D honeycomb bi-crystal consisting of boron nitride (BN) and aluminum nitride (AlN) with periodic dislocation arrays placed at the interface. Throughout this paper,the convention is to useaandbto denote the properties of crystals above and below the interface,respectively. Thus,aandb,μaandμb,andνaandνbdesignate the lattice parameters, shear moduli, and Poisson’s ratios,respectively. According to the periodicity of misfit dislocations,the parametercof a reference lattice is defined as[5]
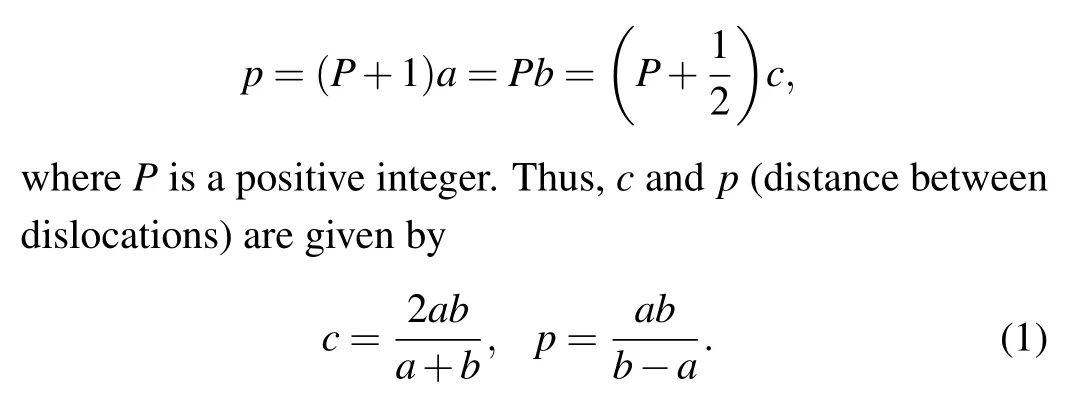
However, there is no geometric relationship similar to Eq. (1) in the direction of the interfacial distance. The distancedis between the two atomic planes on either side of the interface and depends on the bond strength between atoms at the upper and lower planes. A Cartesian coordinate system is chosen with the positivey-axis extending along the normal direction of the interface in the upper half-crystal, and thexaxis along the direction of the slip plane,as shown in Fig.1(a).Variations in energy with the interface distance can be approximated as


Fig.1. (a)Glide dislocations in the adhesive interface between semi-infinite crystals of BN and AlN with different lattice constants. (b)A reference lattice with the parameter c,generated from the lattice parameters a and b with uniform stretching and compression in the two semi-crystals.
whered0is the equilibrium distance, ande0is the formation energy wheny=d0. The parametersVs,Vl, andξare determined from the results of numerical fitting. As illustrated in Fig. 1(b), the reference lattice with parameterscanddcare obtained using Eqs.(1)and(2),and the generalized stackingfault energy that considers the effective interaction between the two dissimilar semi-infinite crystals is calculated.
The proposed method is applied to investigate misfit dislocations under the assumption that the interfacial spacing of the reference latticedcdoes not change compared to that of the heterojunction.[11,12]This assumption works well for shuffle dislocations where the distance between mismatch planes is large. However, the bonds will be greatly distorted in the core for glide dislocations at mismatch interfaces with narrow width. To release the energy generated by bond distortions,especially for small interfacial distances,it is necessary to consider changes in the interaction energy as the interfacial spacing varies. The conventional method is used to calculate the generalized stacking-fault energy for the reference lattice
where the rigid translation can be horizontal or vertical slip displacements,which are relative to the cut plane. Therefore,theγ-surface (interaction energy per unit area) is defined as a 2D function of the relative displacements=(srx,sry). According to the relationship between the interfacial distance and energy and considering the interfacial atomic arrangement of two semi-crystals,theγ-surface can be expressed as


The periodicity of theγ-surface can be expanded into a Fourier series,and the third-order approximation is based on the convergence characteristics of theγ-surface of glide dislocation,which can be described by

whereδ1andδ2are dimensionless parameters to correct the energy along the slip plane. Here the relative displacement of the slip plane (srx=0) corresponds to the unstable equilibrium state, andγmis the height of the barrier. Thus, theγ-surface provides useful information about the core structure of the misfit dislocation and energy.
To verify the theoretical results, the glide dislocations in a BN/AlN heterojunction are numerically simulated using the Viennaab initiosimulation package(VASP).The ion–electron interactions are handled using the projector augmented wave(PAW) method[21]in the generalized gradient approximation(GGA)of the Perdew–Burke–Ernzerhof(PBE)exchangecorrelation functions.[22–24]The plane-wave kinetic-energy cutoff is 600 eV, and the relaxation of the electronic degree of freedom is halted when the total energy change is smaller than 10-6eV. To prevent interactions between inter-layers, a 20 ˚A vacuum spacing is used to simulate the single-layer case.Thekpoints are chosen as 17×1×1 for the reference lattice. For the BN/AlN heterojunction, thekpoints are chosen as 3×1×1 Monkhorst–Pack meshes due to the large size of the supercell. For the reference lattice and the BN/AlN heterojunction, we add a hydrogen bond saturation treatment to eliminate edge influences.
The lattice parameters of BN and AlN are 2.513 ˚A and 3.127 ˚A,respectively. Based on Merwe’s definition of the lattice parameter for the reference lattice, we selectc=1.11a.From Eq.(2),dc=0.675 ˚A represents the interfacial distance from the reference lattice shown in Fig. 2(a). As an approximation to the effective interactions of the BN/AlN heterojunction, Fig. 2(b) shows the results for theγ-surface using the numerical calculations based on density functional theory,and the corresponding parameters obtained from the fitting of Eq.(3)are shown in Table 1.
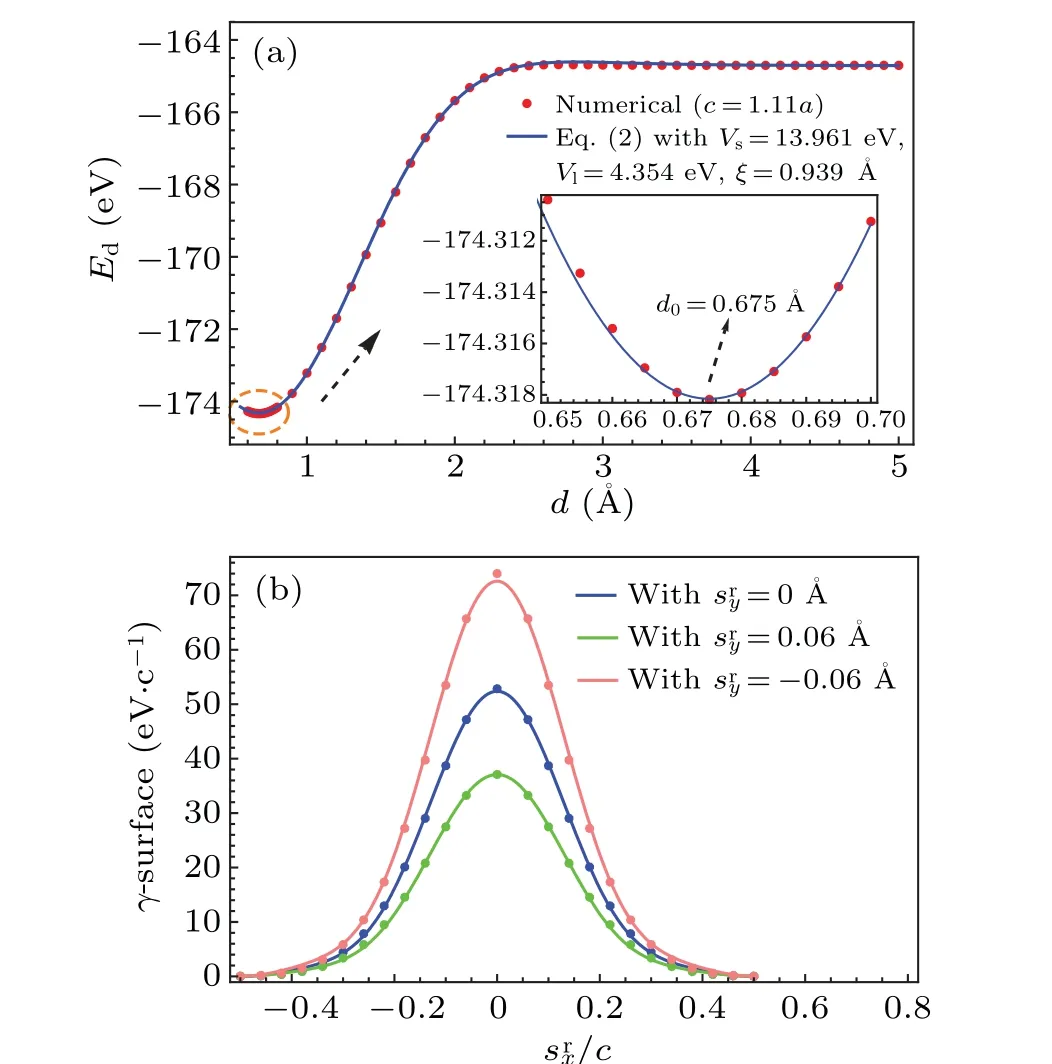
Fig. 2. (a) Energy variation as a function of the interfacial distance d for c=1.11a. The solid line is given by Eq.(2),and the discrete dots are given by first-principles calculations. (b)Characteristic γ-surface in units of eV/c plotted as a function of the relative displacement(srx,sry)between two semiinfinite crystals given by cutting the reference lattice along the slip surface.The vertical displacement sry is measured in the bond length dc =0.675 ˚A,c=2.789 ˚A is the lattice parameter. The solid curves are given by Eq.(3),and the discrete dots are obtained from first-principles calculations.

Table 1. Parameters for Eqs.(1)–(3)and Eq.(5).
3. Structure and energy of misfit dislocations
Following the original P–N theory, dislocations occur at the interface where two semi-infinite lattices are glued together. The boundary displacements for the upper and lower semi-infinite materials are denoted asuajandubj(j=x,y),respectively. To describe the interfacial atomic configuration,we introduce the relative and mass center displacements as


Considering two dissimilar materials with different lattice constants,the dislocations are arranged periodically at the latticemismatched heterointerface in Fig.1(a).Thus,the relative displacement of interfacial atomsurj(j=x,y) as periodic functions satisfies

The relative displacement of the reference latticesrxis often referred to as the plastic displacement, which is parallel to the Burgers vectorb. The dislocation is a topological defect characterized by the Burgers vector whose densityρis defined as dsrx/dx,and the distribution of infinitesimal dislocations is satisfied by

The integral terms in the misfit dislocation equations describe the long-range interactions,which include the elastic effect inside semi-infinite lattices. Compared with Yaoet al.[9]and Zhanget al.,[12]Eq.(10) contains the second derivative modification of the results for the continuum elasticity theory.The appearance of the second derivative term reflects the discrete nature of the crystal lattice,which is generated by shortrange interactions between atoms at the heterointerface. The upper and lower semi-infinite crystals are BN and AlN glued together along the interface between narrowly(widely)spaced atom chains,which results in glide(shuffle)dislocations. For glide and shuffle dislocations, surface chains are different,which causes the second-order expansion coefficients to differ significantly. With reference to the results of the elastic constant (Poisson’s ratiosνa=0.229 andνb=0.461, and shear moduliμa=111.44 N/m andμb=38.92 N/m),we list the relevant parameters in Table 2 from the equations.This improved P–N equation is a nonlinear integro-differential equation and is difficult to solve analytically like the equations in Refs.[4,9].Considering thatsryis sufficiently small so that it can be ignored in Eq.(10),and the boundary conditionssrx(-p/2)=c/2 andsrx(p/2)=-c/2 are satisfied,this dislocation solution can be expressed as

where the dimensional parametersk,δm, andδnare small modifications to the solution of the improved P–N equation.These parameters can be determined by fitting to this equation,as shown in Fig.3(a). When the parameters arek=1,δm=0,andδn=0, this is the exact solution to the misfit dislocation equation constructed by Yaoet al.[9]To present the contributions of the second derivative term,the parametert(t >0)is generated from the solution of the improved misfit dislocation equation,which is defined by

From the solution of Yao’s equation,[9]the characteristic scale isζ=0.126 ˚A whent=1.00, whereas for the solution of Eq. (10) has a characteristic scale ofζ= 0.287 ˚A whent= 0.13. The characteristic scale of the misfit dislocation under the second-order correction is more than double from before the correction. This illustrates that when discreteness corrections are included,the solution of the misfit dislocation is corrected near the dislocation core. The dislocation density illustrates the difference between the solutions of the two equations,as shown in Fig.3(b).

Table 2. The parameters(N/m)for Eqs.(10)and(11).

Fig.3. (a)For glide dislocations,the left-hand side(red dashed curve)and right-hand side (blue solid curve) from Eq. (10) are compared for the fitting parameters of k=0.81, δm =-0.90, and δn =-0.02. The green solid curve represents the expression from Yao et al.[9] without discreteness correction. (b)Application of the dislocation solution(srx)and the dislocation density(ρ)to compare the differences between Yao et al.[9] and Eq. (10). The red dashed curve represents srx and ρ of Eq.(10)for Ω(2)xx /=0,and the green solid curve is for Ω(2)xx =0.
Compared with shuffle dislocations,[11,12]two bonds break during the slip processes for the glide dislocation, and theγ-surface is much higher. This causes great compressive stress in the tangential direction of the interface and concentrates on the dislocation core,and the effect on the normal direction cannot be simply neglected. Equation(11)represents the influence of periodic interface mismatches on changes in the interface spacing. According to periodic misfit dislocation in relation to spatial variations, we assume that the changed form of the interfacial spacing is

The dimensional parameterscy1,cy2,g1,...can be determined by fitting to Eq. (11), as shown in Fig. 4(a). In Fig. 4(b), the relative displacement along the normal direction of the interface can be obtained by using these parameters. Merwe applied the generalized stacking-fault energy of the reference lattice to replace the interface interaction energy for two semiinfinite crystals.[4]This assumption ignores the differences in the equilibrium of the interface distance between the crystals.Considering the relationship between the displacement of the mass center and the relative displacement,these terms can be expressed as



Table 3. The parameters for Eqs.(15)and(16).


Fig. 4. (a) The component of the normal stress to the adhesive interface,which is much larger at the dislocation core and falls off rapidly as the distance increases. The associated normal stress is drawn, and the fitting parameters(cy1=0.001,cy2=0.091,g1=5.2,cy3=0.056 and g2 =35.0) are obtained by comparing the left-hand side (red dashed curve)and right-hand side(blue solid curve)of Eq.(11). (b)Change in interfacial spacing induced by misfit dislocation.

Fig.5. (a)The BN/AlN heterojunction consisting of an upper semi-crystal of BN and a lower semi-crystal of AlN glued together along a given surface and adding hydrogen-bond saturation treatment at the boundary. The small solid circles represent the atomic positions given after relaxation. (b) The theoretical and numerical results for the interface displacement of the a-plane(above misfit interface) and b-plane (below misfit interface) in comparison.(c)The red and blue solid curves represent the theoretical predictions for the displacements of the interface atoms uaj and ubj (j=x,y), respectively, and the gray and green dots represent the numerical results along the x and y directions,respectively.
Here,scyrepresents the plastic deformation along the interfacial spacing direction when dislocations are in the periodic arrangement of the heterointerface. As the interfacial distance of the heterojunction(d)is different from that of the reference lattice(dc), the mass-center displacement along they-axis is

As is shown in Fig. 5(a), the interfacial atomic configuration is evaluated from first-principles calculations after full relaxation. The definition of the dislocation width indicates that narrow dislocations will cause large compressive stresses at the coordinates of the dislocation core, which induces bending deformation at the interface. To verify the accuracy of the theoretical predictions for interfacial displacements based on the relationship between the mass-center and relative displacements, we compare the results with the first-principles calculations in Figs.5(b)and 5(c). The theoretical results are close to the numerical results for the interface atomic displacement,which indicates that the theory can be widely used to investigate misfit dislocations.
The energy of misfit dislocations contains contributions from both the elastic strain energy and misfit energy, and the characteristic width of the dislocations depends on the results of the competition between them. These contributions are expressed in terms of the energy per unit length due to the periodic arrangement of misfit dislocations. Following the classical P–N theory,the boundary equilibrium equation at the interface provides the elastic strain energy through the variational formulation,which is written as
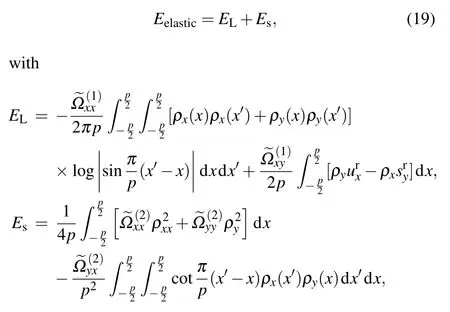
whereρx= durx/dxandρy= dury/dx. The first term ofELprovides the elastic energy from long-range interaction based on the dislocation distribution from the elastic continuum theory and the superposition principle because the stress out of the dislocation core is slowly varying. The second term ofEscomes from discrete corrections at the interface. By substituting the solutions to Eqs. (10) and (11), the two terms of the elastic energy are

Here,the parametersm=(1+δm)gandn=(1+δn)g. If the dislocation is regarded as a superposition of each infinitesimal dislocation,then the misfit energy is attractive and causes the dislocations to condense into nucleation. The misfit energy can be written as

However, it is difficult to calculate the energy of misfit dislocations from first-principles calculations and to verify the accuracy of the theoretical results. As heterointerfaces greatly influence the properties of composites, theoretical studies have focused on understanding the microscopic mechanism that controls the strength and fracture of composite materials.Here,we introduce the theoretical adhesion work written as



Table 4. Energy of shuffle and glide dislocation(eV/˚A).
4. Summary
Periodic pentagon-heptagon defects are glide dislocations located between narrowly spaced atom chains at mismatched interfaces,which gives a discrepancy between glide and shuffle dislocations for interfacial interactions. Based on the definition of the restoring stress in the original P–N theory, a generalized stacking fault energy for the reference lattice is introduced as an effective interaction for the heterointerface.The approximate solution of the nonlinear integro-differential equation(improved P–N equation considering lattice discrete correction) is obtained based on Merwe’s solution. This approximate solution clarifies the characteristic width of the dislocation and estimates the effect of the compression force on the normal direction. When approximating the interface interaction energy,Merwe ignored the differences between the interfacial spacing of the heterojunction and reference lattice.To predict the interfacial atomic coordinates with a high accuracy,the relationship between the mass center displacement and relative displacement is slightly modified. The core structure of the misfit dislocations and the interfacial atomic configuration in BN/AlN heterostructures are detailedly expressed through the improved P–N equation, which is reliable compared with the results from first-principles calculations. The energy of misfit dislocation has two components: the energy of the elastic strain and the misfit energy. For larger misfits, interface atoms with a single-bond connection have a second-order correction along the tangential direction that greatly influences the elastic energy,while the normal displacement has no influence.Thus,the misfit energy provides the primary component.With a considerable impact on changes in the interfaces spacing when glide dislocations exist at the interface, the associated effect on the dislocation energy is compared with shuffle dislocations in Table 4. The elastic strain energy becomes an important term due to the interactions between the tangential and normal directions at the glide dislocation with a narrow interfacial spacing. Here, we verify the accuracy of the theoretical value by applying the correlation of the adhesion work with the energy of misfit dislocations and show that the structure for glide dislocations is more stable than that of shuffle dislocation based on the magnitude of the adhesion work.
Appendix A: Coefficients for the improved Peierls–Nabarro equation
According to previous studies on misfit dislocations, the lattice discreteness effect is considered to be caused by surface effects in the improved Peierls–Nabarro (P–N) equation.[11]The parameters are expressed with the properties of materials(Poisson’s ratioνand the shear modulusμ)as

It is noted that the subscriptsaandbdistinguish the elastic constant of the upper and lower semi-infinite crystals,respectively. The discrete parametersβaandβbare related to the atomic arrangement of the interface where the dislocations are.For the surface chain of glide dislocations, these can be expressed as[13]

Appendix B: Transformation of the integrand function
Since the relative displacement and dislocation density are periodic functions, they describe the periodic dislocation array at the misfit interface. To facilitate the description of the transformation process of the integrand of the misfit equations,we usef(x)and df(x)/dxto represent periodic functions for Eqs.(8)and(9),respectively. The details of the derivation are given as follows:
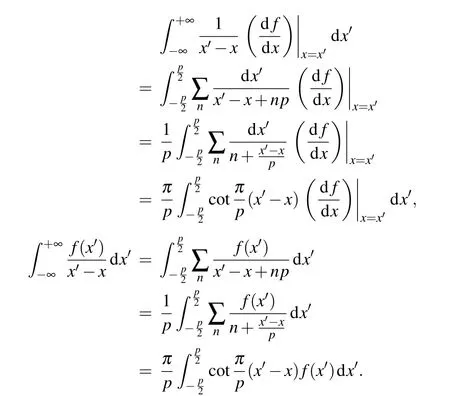
- Chinese Physics B的其它文章
- A design of resonant cavity with an improved coupling-adjusting mechanism for the W-band EPR spectrometer
- Photoreflectance system based on vacuum ultraviolet laser at 177.3 nm
- Topological photonic states in gyromagnetic photonic crystals:Physics,properties,and applications
- Structure of continuous matrix product operator for transverse field Ising model: An analytic and numerical study
- Riemann–Hilbert approach and N double-pole solutions for a nonlinear Schr¨odinger-type equation
- Diffusion dynamics in branched spherical structure

