全概率公式与贝叶斯公式应用探析
冯广庆,韩春阳
(河南理工大学 数学与信息科学学院,河南 焦作 454000)
1引言
随着社会的高速发展,概率论与数理统计在诸多领域展示了独特的魅力.目前,人工智能、大数据分析等领域已渗透概率统计的思想.深入透彻研究这些实际问题,要借助概率统计知识,建立数学模型,处理和分析数据,对问题做出推断和预测.全概率公式和贝叶斯公式是概率统计课程的两个十分重要的公式,是基于条件概率发展而来的求概率的工具[1].在生产生活中,可以归类于条件概率的情况很多,但大多数较复杂,基于条件概率的全概率公式和贝叶斯公式相继应运而生,它们利用已知信息使问题化繁为简,提供了解决复杂事件概率问题的有效途径[2].
2公式解释
全概率公式和贝叶斯公式一般用于求几个事件同时发生的概率,从公式的形式来看,实质上是乘法公式的求和,它们的存在是条件概率思想的进一步反映,这两个公式既相互联系又有所区别[3-4].
全概率公式提供计算复杂事件概率的行之有效的途径,体现了结果的发生与每个原因的关系,是一个根据原因寻找结果的过程.全概率公式对复杂事件中的每个方面分类讨论,逐个击破求出总概率,解决的是多种情况下造成同一种结果的概率.实际问题中的“结果”的概率不易求得,但导致该“结果”发生时的每个“原因”的概率容易找到,依次逻辑可将计算一个复杂事件的概率问题化繁为简.贝叶斯公式表示的是在特定条件下一个事件的概率,通过已经发生的结果寻找导致这个结果发生的原因,探究最可能导致某个复杂事件发生的可能性最大的原因.贝叶斯公式也可用于计算后验概率,通过事件的发生这个新信息,对事件的概率做出修正,重新认识之前的概率,做出新的判断.在实际应用中,利用贝叶斯公式重复估计某个事件的概率从而计算出新的后验概率,可以达到提高所求概率的准确性的目的.
3案例分析
全概率公式与贝叶斯公式是概率统计的重要内容,与实际生活联系紧密[5-6],本文列举7个案例阐述它们的应用.
3.1寻找物品案例
某同学银行卡丢失,他把丢失银行卡的地点锁定为宿舍、宿舍到银行的路上、银行.假设银行卡掉在宿舍、路上、银行的概率分别是10%、30%、60%,而掉在上述三个地方被找到的概率分别是0.4、0.3和0.5.试求该同学找到丢失的银行卡的概率是多大.
解析:根据题设找到银行卡有三种情况,而每种情况的丢失概率和被找到的概率都已知.所以找到银行卡的概率是这三种情况的累计和,符合全概率公式“多个因素作用于某个事件”的情况.将事件A1,A2,A3分别设为“掉在宿舍、掉在路上、掉在银行”,将B记为“银行卡被找到”,根据全概率公式即可求出P(B):
P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)+P(A3)P(B|A3)
=0.1×0.4+0.3×0.3+0.6×0.5=0.43
即该同学找到银行卡的概率是0.43.
这是全概率公式的一个简单应用,通过上述计算除了知道该同学最终能找到银行卡的可能性有多大,另外也不难看出,与其他两种情况相比,该同学在银行找到银行卡的可能性最大.受寻物问题的启发,我们在实际的搜救和追踪问题上,也可以运用全概率公式的这种思想梳理问题中的有效信息,估计问题发生的可能性,为设计问题的解决方案提供参考.
3.2产品质检案例
一批新生产的手机优等品率为85%,由于电子产品对质量要求较高,需要检验员质检,但人工质检难免会存在一定的误差.为了把质检过程中的误差最小化,分派三名质检员组成质检小组对这批手机的质量进行质检,规定这三个质检员中至少有两个检验员认为是优等品,最终才能被确定为优等品.假设检验员之间的判断相互独立,每个检验员能够把真正的优等品认定为优等品的概率为96%,而将非优等品认定为优等品的概率为3%,那么该质检小组最终能够认定出真正的优等品的概率是多少?
解析:要计算被认定为优等品的产品确实为优等品的概率,即求的是条件概率,需要利用贝叶斯公式求解.设A表示“产品为优等品”,B表示“质检时产品为优等品”,那么所求概率为P(A|B).
首先计算P(B),分析可知事件B的发生是有前提条件的,即在对优等品或非优等品进行检查时,三个人中至少有两个人认为是优等品.因此计算P(B)用全概率公式:

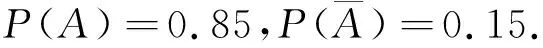
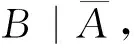
X~B(3,0.96),Y~B(3,0.03)
那么
所以

=0.85×0.995328+0.15×0.002646
=0.8464257
故所求概率为
结果表明,质检小组最终能够认定出真正的优等品的概率为99.95%.
在这个问题中,全概率公式只发挥了部分作用,需要结合条件概率以及概率分布才能得到有价值的信息.这说明在实际问题中,要灵活利用其它概率论知识才能更好地解决问题.全概率公式广泛应用于实际生产中,把复杂事件的概率分解为简单事件概率的和,有助于计算出不易直接求解的概率.全概率公式在不讲求次序的随机情况下能够计算具有多种情况的复杂事件.根据生产产品的数据统计,利用全概率公式预测产品的合格情况、在数据层面上检测产品的品质情况等,是全概率公式应用于实际生产比较多的一个方面.
3.3调查敏感问题案例
调查敏感问题,不易得到调查者的配合,需要设计一种调查方案,使被调查者确信参加调查不会泄露个人秘密,可以没有顾虑地做出真实回答.以考试作弊为例,方案设计如下:为被调查者提供一个密闭环境,在被调查期间不会有其他人进入,被调查者只需要按照操作回答问题即可.第一步:被调查者从只装有黑球和白球的盒子中随机摸出一个球,盒子里有u个黑球,v个白球,看过颜色后立即放回.第二步:如果被调查者摸到白球,则要回答问题1,即“你是否喜欢红色?”;若被调查者摸到黑球,则回答问题2,即“你是否在考试中有过作弊行为?”.被调查者无论是回答问题1还是问题2,都只需在空白纸条上是写下“是”或者“否”,然后再把纸条放入密封的投票箱.
解析:设收到的纸条总数为n,其中k张纸条上写了“是”.任意选择一个被调查者,他喜欢红色的概率为0.5,盒子里黑球数和白球数是已知的.
现在根据调查数据估计受调查学生考试作弊的比率p.记事件A为“摸到黑球”,B为“摸到白球”,C为“回答“是”的纸条”,则
由全概率公式得
即
在一次实际调查中,结束后总共收到了1583张有效答卷,其中有389张答卷回答“是”.罐子里黑球的个数为60、白球的个数为40.由以上方案和调查数据计算得到
综上所述:大约有7.62%的学生在考试中有作弊行为.
方案完美体现了全概率公式的巧妙之处,在调查敏感性问题时,直接调查的结果可信度比较低,需要设计一个能够让被调查者给出真实想法的方案.在调查方案中,会出现与所调查的问题无关的其他问题,但这个无关问题的情况是我们已经掌握的,也就是已知条件.全概率公式的特点就是能够通过事件的已知条件计算一些不能直接计算的概率.设计调查方案时,从可以计算出概率的问题出发,把它作为目标问题的条件,然后再把方案向目标问题延伸,最终巧妙地得到想要的调查数据.
3.4保险投保案例
保险公司将新险种的投保人划分为两类,一类为容易出事故者,另一类为安全者.根据统计研究可知:一个易出事故者在一年内发生事故的概率为0.45,而一个安全者发生事故的概率为0.1.如果投保人在投保期间发生了事故,能向保险公司申请理赔.假设第一类人投保此险种人数所占的比例为18%.现有一个投保人来投保此险种,那么该投保人在购买保单后一年内将申请理赔的概率有多大?


=0.18×0.45+0.82×0.1=0.163
结果表明:该投保人在购买保单后一年内将会申请理赔的概率为0.163.
概率论在保险领域应用广泛,保险公司可以依据概率论知识合理制定险种,降低理赔风险从而获得盈利,被保者可以依据概率论知识购买保险最大化降低知识造成的损失.全概率公式可以在保险精算的模型中发挥一部分预测作用,为保险公司设计不同的保险方案提供参考,也可以在被保者投保过程中确定险种对自己是否合理,以及预测保险的回报问题,决策出购买合理的保险种类.
3.5普查疾病案例
据调查,某种疾病在某地区的发病率为0.0003,现在对该地区自然人群进行普查.已知该疾病可通过抽血化验筛查,医学研究表明,该化验结果会有存在错误的可能.根据以往的临床记录,患有该疾病的人其化验结果99%呈阳性(患病),而没患病的人其化验结果99.9%呈阴性(不患病).现有一个人的检查结果呈阳性,那么他真正患病的概率是多少?
解析:记A为事件“化验结果呈阳性”,B为事件“被检查者患病”,则

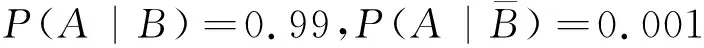
在该问题中的所求概率为P(B|A),由贝叶斯公式得
=0.229
结果表明,在化验结果呈阳性的人中,真正患病的人不到30%.
已知该疾病的发病率为0.0003,即10 000人中大约有3人患病,大约有9 997人不患病.其中3个患病者的化验结果呈阳性的约是3×0.99=2.97.另外9 997个不患病者的化验结果呈阳性的人数约是9997×0.001=9.997.因此12.967个化验报告呈阳性的人中有2.97个人是真正患病,其比例约为22.9%.显然,这个数据存在令人质疑的地方,利用这个数据将会出现错误的判断.
该处检验数据出现了不能准确反映实际的情况,说明该调查的检验精度远远不够.为了减小错误率,患病普查工作经常采用复查的方法.如果对首次化验结果呈阳性的人群再进行一次复查,此时该群体的发病率已经提高为P(B)=0.229,利用调整后的发病率再次使用贝叶斯公式计算患病概率得
=0.997
经过连续两次利用贝叶斯公式求患病概率后,普查的患病概率准确度明显提高了很多.
该案例表明:仅依靠疾病在人群中表现出的已有信息对疾病做出诊断并不能得到准确的结果,这个结果只是患病的先验概率.把得到的先验概率加入贝叶斯公式的计算中继而得到后验概率,即通过贝叶斯公式对先验概率做出修正后,准确率会大大提高.该案例阐述了如何利用概率论知识对现代医学的调查结果做出精准有效的解读.
3.6根源案例
某种奶制品由三家制造厂加工(表1),假设这三家制造厂的产品在仓库中是均匀混合的,没有明显的区别标志.在仓库中随机取出一件,若取到的是一件次品,那么这件次品最有可能来自哪个制造厂?
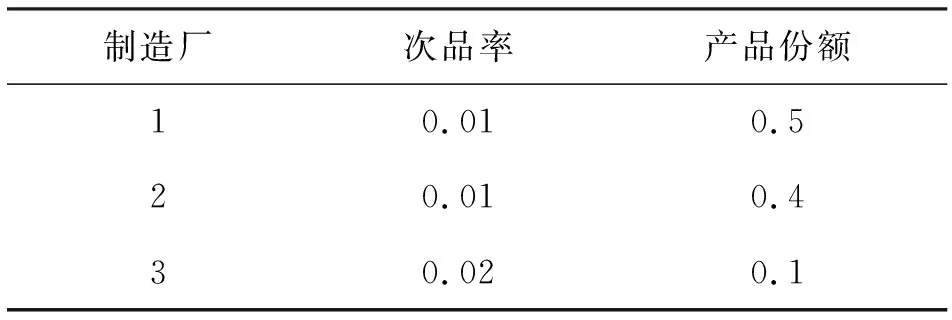
表1 不同制造厂奶制品次品率及产品份额
解析:设A表示“随机取一件,取到的是一件次品”,Bi表示“所取到的奶制品是来自第i制造厂”(i=1,2,3).为了分析取出的这件次品最有可能来自哪个制造厂,需要根据次品率求出这件次品由三家制造厂生产的概率分别是多少,这显然是一个贝叶斯问题.
首先利用全概率公式求解P(A)
P(A)=P(A|B1)P(B1)+P(A|B2)P(B2)+P(A|B3)P(B3)
=0.01×0.5+0.01×0.4+0.02×0.1
=0.011
然后,根据贝叶斯公式
以上结果表明,这件次品来自第1家制造厂的可能性最大.
这是贝叶斯公式通过事件的已知结果探究最可能导致事件发生原因的一个实际应用,根据题目中的数据来看,制造厂3的次品利率最高,但因为供货份额最低,所以在随机抽查的情况下抽到次品的概率反而最低.而制造厂1的次品率低,但是供货所占的份额最多,导致在随机抽查的情况下抽到次品的概率最高.经销商可以根据这些数据做进一步分析,适当调整代工方案或者更换工厂.
4结语
全概率公式和贝叶斯公式作为概率论中的两个极具代表性的理论,能够解决许多实际问题,预测某些事情的趋势或前景,对生产生活有很大的指导意义.全概率公式体现了“面面俱到”“化整为零”的思想,把一个复杂事件拆分成简单事件的和,在用贝叶斯定理解决问题时,要通过先验概率才能求出最后的后验概率,其实也是一个对某事件发生的概率做出修正的过程.在实际问题中只需要根据事件已知的部分信息再加以计算,就能够把更多关于该事件的数据和具体分析呈现出来.无论是这两个公式还是课程中其他的理论,它们不仅仅是抽象的数学符号,还是简洁的规律揭示,了解它们只是一个开始,熟练地应用它们才是最终的目的.

