离散型随机支付未定权益的套期保值策略研究
郭建华
(邵阳学院 经济与管理学院,湖南 邵阳,422000)
任何风险投资都是在随机环境中进行,因而,如何降低随机环境中未定权益风险是金融界的研究热点。风险的度量准则众多,其中,HANS等[1]提出将投资组合成本的条件均方误差过程E[(CT-Ct)2|Ft]作为一种风险度量方法;BOUKEAU等[2]提出均方准则,即把终期财富与未定权益之差的平方的期望,即E(VT-H)2作为风险,后来,均方风险准则被广泛应用于金融领域[3],但这种风险定义方法与实际风险含义有所违背,为克服上述准则的不足,FÖLLMER等[4]在自融资约束下提出用期望亏损E(H-VT)+作为衡量风险的标准;此外,还有诸如成功概率标准[5]、VaR标准[6-9]等。然而,这些文献研究的都是标准欧式未定权益的套期保值问题,很少涉及非标准欧式未定权益。而实际情况是,在金融市场上非标准欧式未定权益很常见,譬如投资者出售某种金融合约(如不同期限的期权、保险合约等)而且在某一时间段内可能面临着随机的支付义务(期权到期的随机损失、保险赔付),目前很多研究者对这种随机支付型未定权益[10-11]套期保值问题展开了深入的研究,THOMAS[12]研究了资产价格是连续鞅情况下随机支付型未定权益的风险最小套期保值;杨建奇等[13]研究了对完全信息和不完全信息下随机支付型未定权益的风险最小套期保值;文献[14]利用G-K-W分解定理研究了随机支付未定权益的风险最小套期保值。
本文以成本的条件均方误差过程作为风险度量,建立风险最小套期保值模型,研究了离散型随机支付未定权益风险最小动态套期保值。对一个离散型随机支付未定权益,首先利用G-K-W分解定理证明其存在唯一最小风险策略;然后根据最优性原理,利用动态规划方法求得套期保值期内每一策略调整时刻的最优策略的显式解。
1 套期保值模型
设(Ω,F,P)是概率空间,F=(Ft)t=0,1,…,T表示市场信息流,S=(St)t=0,1,…,T为非负的F适应过程,表示风险资产(股票)价格,B=(Bt)t=0,1,…,T表示无风险资产(债券)价格。为了计算方便,本文假定价格均为折现值,即Bt≡1,St为股票的折现价格。H={Ht,t=0,…,T}是一个平方可积随机支付流,表示投资者出售某种金融合约(如不同期限的期权、保险合约等)而在[0,T]时间段内不同时刻可能面临的现金支付(期权到期的随机损失、保险赔付),即投资者可能面临一个随时发生的随机损失,这里假设(t-1,t]内发生的随机支付都累积到t时刻完成并记Ht=H(t,St)。为了避免或减少这种损失的发生,套期保值者通常利用现有的金融资产构建一个投资策略来降低这种损失。
假设对任意随机过程Y=(Yt)t=0,1,…,T,Θ(Y)表示所有满足ϑtΔYt∈L2(P),t=0,1,…,T的可料过程(ϑt)t=0,1,…,T构成的空间,其中,ΔYt:=Yt-Yt-1。
定义1:一个投资策略φ就是一对随机过程(ϑ,δ),其中,ϑ∈Θ(S),δ是适应过程,且:
Vt(φ):=ϑtSt+δt∈L2(P),t=0,1,…,T
(1)
式中:V(φ)称为是投资策略φ对应的价值过程。其中,(ϑt,δt)表示在时刻t做出策略调整后投资者持有的股票份数和债券金额,相应地,Vt(φ)表示t时刻策略调整后的资产组合的理论价值。
定义2:对于随机支付流H={Ht,t=0,…,T},和给定的初始组合(ϑ0,δ0),称一个策略φ=(ϑ,δ)是自筹资策略并完全复制H,如果ϑtSt+δt=ϑt-1St+δt-1-Ht,其中,Ht表示在(t-1,t]发生的随机支付。
注:1)由于实际市场的不完备性和金融资产交易费用的存在,因而通过自筹资策略对未定权益进行完全复制是难以实现的,也就是要达到完全复制未定权益就必须突破自筹资约束而追加成本;
2)根据定义1和定义2,在任意时刻t做出策略调整时,随机支付Ht已经发生,所以,在期末T时刻,认为未定权益已经支付完成,有理由认为H的完全复制策略φ对应有VT(φ)=0,并称φ为0-取得策略。
根据定义2的注(1),要复制H则需要追加成本,这样,在每两次策略调整时间段(t-1,t]内,有如下费用发生和组合的变化:
组合由t-1时刻的Vt-1(φ)=ϑt-1St-1+δt-1调整为t时刻的Vt(φ)=ϑtSt+δt;
时间段(t-1,t]内发生的随机支付Ht;
时间段(t-1,t]内由于资产价格的变化引起的组合价值增量ϑt-1ΔSt:=ϑt-1(St-St-1);
时间段(t-1,t]内追加的成本ΔCt(φ):=Ct(φ)-Ct-1(φ);
而且上述费用满足关系:Vt(φ)=Vt-1(φ)+ϑt-1ΔSt+ΔCt(φ)-Ht,即
Ct(φ)=Vt(φ)-Vt-1(φ)-ϑt-1ΔSt+Ct-1(φ)+Ht
(2)
把式(2)关于时间0,1,…,t做累加,有:
定义3:交易策略φ=(ϑ,δ)对应的成本过程为
C0(φ)=V0(φ)+H0=ϑ0S0+δ0+H0
(3)
ΔSj=Sj-Sj-1,分别是股票的价格增量。因为投资者是在0时刻售出未定权益并建立对冲头寸,故通常认为H0=0。
定义4:交易策略φ=(ϑ,δ)对应的风险过程定义为
Rt(φ):=E[(CT(φ)-Ct(φ))2|Ft],t=0,1,…,T
(4)
定义5:设φ={(ϑt,δt)},t={0,1,…,T}是一个策略,如果对任意可容许策略φ′={(ϑt′,δt′)}:①VT(φ)=VT(φ')P-a.s;②对s≤t,ϑs=ϑs′;③对s 在风险最小标准下,寻找一个0-取得策略对未定权益(随机支付流H={Ht,t=0,…,T})进行套期保值,则套保模型可表示为 (5) 定理1:任意风险最小策略φ=(ϑ,δ)对应的成本过程Ct(φ)是鞅[15]。 定理2:对于任一给定的离散型随机支付未定权益H={Ht,t=0,…,T},存在唯一的0-取得风险最小策略φ=(ϑ,δ)。 证明:存在性: (6) 设φ=(ϑ,δ)是一个0-取得策略,即VT(φ)=0,则由定义3及式(6)得: (7) (8) 唯一性: 定理3(最优性原理[16]):对任何(t,x)∈[0,T]×R以及s∈[t,T],下述等式恒成立: (9) 式中:yt,x(.)=yt,x(.,u(.))是过程的状态,u(.)∈U[t,T]是控制过程,U[t,T]是时间集[t,T]内的可选控制集。 定理4:公式(5)对应的套期保值问题有如下形式的最优策略: (10) 证明:在0-取得策略约束VT(φ)=0下,由定义3,可得 (11) 用归纳方法证明定理4。 当t=T-1时: (12) 当t=T-2时: (13) 可以解得: (14) 假设在t+1时刻,有: 则在t时刻,有: (15) (16) 证毕 保险公司为了减小可能面临的保险支付则会购买相应股票或债券进行风险对冲,根据定理4,各时刻的对冲头寸为 (17) (18) 对一个离散型随机支付未定权益,首先证明其风险最小套期保值策略是一个鞅过程,然后利用G-K-W分解定理证明其存在唯一风险最小套期保值策略;再根据动态规划原理,利用倒向递推方法推导得出各离散时刻随机支付未定权益的风险最小套期保值策略显式解,该策略可以用风险资产价格和随机支付的条件矩表示。2 模型求解


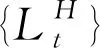

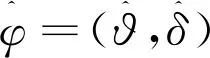




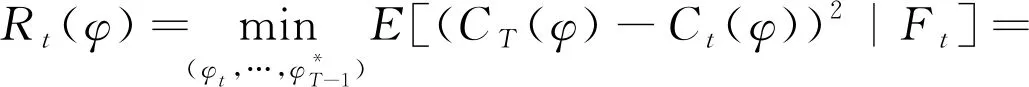

3 一个算例

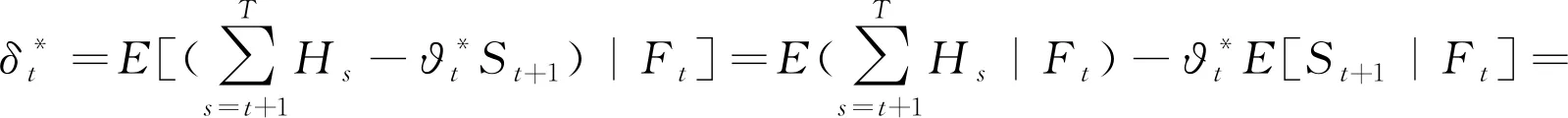
4 结论

