对Keenan 推理模式中量词分类的再研究

郑裕颖

（中国人民大学哲学院，北京 100872）

在日常推理当中，往往存在一些较为常用的推理套路，例如最常见的三段论推理模式：所有希腊人都是勇士，没有勇士会畏惧，所以没有希腊人会畏惧。为了简化我们的判断进程，逻辑学家对这样的推理套路加以抽象，得到相应推理模式：所有(A,B)，没有(B,C)，所以，没有(A,C)。在这个推理模式当中，量词起到了至关重要的作用，如果我们将其中的量词替换掉，将会得到无效的推理。例如：有些(A,B)，没有(B,C)，所以没有(A,C)。针对这个判断，可以举出具体的例子：有些生物是哺乳动物，没有哺乳动物不是胎生，所以所有生物都是胎生。因此，量词可以对推理模式的有效性起到决定性作用，在对任何日常推理做抽象时，都必须对量词做好区分和限定。

如果只凭借直观印象去判断，下面这个推式并非难题：

Keenan 认为[1]，在这个推理模式的条件当中出现的量词就是比例量词。而Westerståhl 则认为，这样的量词应当归类为驻留的右单调递增的量词[2]，而并不限于比例量词。

对于Westerståhl 的分类方式，Keenan（2008）[3]认为Westerståhl 的分类方式尽管看起来更一般，但其实是多余的，因为后者分类方式所包含的量词全部都是比例量词，此外，存在更多的自然语言的推理模式，其中参与的量词是比例量词。但Keenan 并未对后者和原有的比例量词分类之间为何会有范围一致的情况做出解释，因此直接否认单调性的分类方式的理由不够充分。因为我们不免产生疑问：假如二者范围一致，为何不采用后者呢？此外，这两种分类方式是否是等价的？

Westerståhl 虽然证明了其分类方式有效，但并未给出相应的直观依据，因此很难直接看到它和比例量词的分类方式之间的联系，尽管两种分类方式针对的是同一类量词。也就是说，我们已经知道上述有效推理模式当中可使用何种量词，并且已经通过简单的证明确认这些类型的量词当中的确有一部分可保证推理的有效性；但是我们并不知道这种推理模式何以适用于这样的量词，为什么这些类型下的量词可以确保推理的有效性。

本文将比照两种分类方式的优劣，确定二者的关联以及各自的适用场合，并在此基础上给出一个对自然语言推理模式当中的量词归类的一般路径。下文将解释涉及此话题的主要概念，指出Keenan比例量词分类的关键不足，为Westerståhl 的结论给出另一种证明方法：直观的逆推证明法，从而让这个分类方法更有说服力。在从直观角度比照两种归类方式之后，我们发现这二者的联系：它们都建立在数量的基础上。这也从侧面说明了量词与谓词的不同。

一、概念简介

我们这里的量词，指的是广义量词（Generalized Quantifiers），也就是一阶逻辑的全称量词和存在量词的推广，也即不仅限于这二者的量词。我们这里对量词的定义采用了模型论视角下的定义，这一定义由Mostowski 在1957 年首次提出[4]。

定义1 （公式在模型中的扩展）

定义2（量词的类型）

量词的类型指的是一个每个成员都不小于1 的自然数序列τ=〈n1,… ,nk〉。[5]65

比如类型〈1,1〉就是一个有序二元组，它的每一个成员都是1，因此满足“不小于1”的要求。量词的类型主要用于说明在这个量词的数量关系下的论元的类型，是个体集，还是多关系（这里的关系包括映射等复杂的关系）。比如〈1,1〉类型的量词表示的是两个个体集论元之间的数量关系。例如“3 个人吃了苹果”，其中的量词是“3 个……是……”，论元分别是“人”和“吃了苹果的人”这两个个体集。而〈1,1,2〉类型的量词则包含两个论元，且第二个论元是二元关系，例如：“3 个人一共吃了5个苹果”，我们无法说3 个人是“一共吃了5 个苹果的人”，因为这里的意思是“3 个人吃的苹果加起来有5 个”，而不是每个人都吃了5 个苹果。因此这里的数量关系不是单纯的个体集之间的关系，而是个体集“人”、二元关系“……吃……”以及个体集“苹果”三个论元之间的关系。

定义3（任意类型的量词）

一个类型为τ的量词Q给每个域M指派一个M上的k元二阶关系QM，其中QM的第i个论元是M上的ni元关系。则（其中的定义由如下公式给出：

对a1,…,al∈ M ,

结合定义1 和定义2，可以看出，这里的量词也就是对不同的公式给出相应的“解”的集合的有序多元组。也就是说，量词的每一个论元可能出现的情况是一个公式的“解”，由这个公式所定义，而这些论元之间的组合关系就是量词。例如上述例子当中，“吃了5 个苹果的3 个人”、“被3 个人吃掉的5 个苹果”和“……吃……”三者能令句子“3 个人一共吃了5 个苹果”为真的组合情况的合集就是对该句子当中量词的刻画。简言之，量词就是用于限定、刻画这些论元的组合关系的二阶关系。

根据上述定义，类型是一种用于划定量词所涉及的对象的范畴。其中，类型的论元数确定了量词涉及多少个不同类型的对象，每个论元的具体数目确定了每个类型的对象类型是几元组（是单一的个体集，还是更为复杂的关系集或映射集①）。而本文背景介绍当中的推理模式所涉及到的量词是〈1,1〉类型的量词，我们在自然语言中遇到的量词主要是类型〈1〉和〈1,1〉。而根据研究，类型〈1〉的量词可以找到等价的类型〈1,1〉的量词，因此本文只探讨类型〈1,1〉的量词及其表现。为行文方便，下文的量词均指类型〈1,1〉的量词。

须要注意的是，本文所指的〈1,1〉类型的量词不同于谓词表达的二元关系。首先量词主要面对的不是具体个体，而是个体数量，往往可以忽略具体的个体；其次，量词是逻辑常量，而谓词则作为参数出现②。

定义4（比例量词）

一个量词Q 是比例量词（Proportional quantifier），当且仅当对所有的集合A,B,X,Y，如果那么Q(A,B)=Q(X,Y)[5]88。

也就是说，比例量词的两个个体集论元的交集和第一个论元之间的基数数量比例直接决定了比例量词自身的全部意义。通俗和不严格地说，表示两个个体集大小之间的固定数量比例的量词就是比例量词。

抽象地看，单调性（Monotonicity）指的是函数F 的性质，与两个序关系≤1和≤2之间存在如下关联之一：

如果x1≤1x2那么F(x1)≤2F(x2)（单调递增）；

如果x1≤1x2那么F(x2)≤2F(x1)（单调递减）。

具体到量词，上述单调性中的函数对应量词，两个序关系分别对应集合之间的包含关系和量词表达式之间的蕴涵关系。由此，类型〈1,1〉的量词的单调性定义如下：

定义5

类型〈1,1〉的量词QM在第1 个论元上是单调递增的，当且仅当：如果QM(R1,R2)且R1⊆ R1′，则QM(R1′,R2);

类型〈1,1〉的量词QM在第2 个论元上是单调递增的，当且仅当：如果QM(R1,R2)且R2⊆ R2′，则QM(R1′,R2)。单调递减的定义类似。

例如，量词“每一个”就是在第二个论元上单调递增的，因为当我们说“每一个学生都吃水果”时，“苹果”作为第二个论元，它是“东西”的子集，因此我们可以直接得到“每一个学生都吃东西”。因此满足单调性的定义。

量词的单调性不仅限于单纯的递增和递减。对于类型〈1,1〉的量词，就上述定义而言可以直接得到四种单调性，分别是左递增（左边论元上单调递增，记作↑MON，右递增（右边论元单调递增，记作MON ↑），左递减和右递减（定义和记法可类推）。此外，单调性对于拥有同构性（Isomorphic,简写为ISOM）和驻留性的量词而言还有更复杂的种类。

定义6 （驻留性）

类型〈1,1〉的量词Q称为驻留的[6][7]③Conservativity，缩写为CONSERV），当且仅当，对所有的M和所有的A,B ⊆ M，QM(A,B)⇔ QM(A,A ∩B)。

驻留性说的是两个论元的数量关系等价于第一个论元和二者交集之间的关系，颇有一种量词意义全赖A以为生的意味，因为对任何集合B而言，我们不需要考虑B的全体在量词中的表现，而只需要考虑B中属于A的部分，就可确定B与A的关系是否符合该量词。这样的量词是非常普遍的，几乎我们见到的所有自然语言的〈1,1〉类型的量词都具备这样的性质。例如“多数猫是橘色的”,这里的两个论元是否符合量词“多数”的要求，实际上依赖于“猫”这个个体集，我们不关心其他橘色的事物，而只在乎“橘色的猫”。

文中主要涉及到的几个量词相关的运算包括外否定（Outer negation），内否定（Inner Negation）和对偶（Dual）。三者定义如下：

对类型〈1,1〉的量词Q，(¬ Q)M(A,B)⇔并非QM(A,B)(外否定)

(Q¬)M(A,B)⇔ QM(A,M-B)（内否定）

Qd=¬(Q¬)=(¬ Q)¬ （对偶）

例如，“所有人都是老师”，其中的量词是“所有(A,B)”，A是“人”，B是“老师”。那么把它换成它的内否定得到的句子意义应当是：所有人都不是老师。也就是说，内否定的量词等价于“所有(A,)”，也就是“没有(A,B)”。而“所有(A,B)”的对偶就是在内否定上加上外否定，即“并非没有(A,B)”，也就是“有(A,B)”。下一节我们将论证，在上述推理模式中出现的量词“超过(A,B)”的对偶正是“至少”。

二、比例量词分类方式

对于上文的推理模式，我们假设Keenan 的比例量词归类法是合理的，并进一步举例如下：

结论1

对于0≤ p≤ 1的分数p而言，量词“超过p”与“至少1-p”互为对偶。

证明：

令Q代表量词“超过p”，Q′代表量词“至少1-p”。QM(A,B) iffQMd(A,B) iff并非QM(A,M-B) iff 并非p （由A ⊆ M） iff

根据上述分析，我们可以抽象得到更为一般的推理模式(1)如下：

其中的sоmе(A,B)意为有些A是B，即：sоmе(A,B)iff A ∩ B ≠Ø; M是量词作用的域。

那么，是否所有的比例量词都可以有上述对偶关系呢？从比例量词的定义可以看出，的值直接决定了比例量词Q(A,B)的意义，我们用a表示的值，比例量词中的分数的值记作p，则一个比例量词可能出现的a,p关系代表了比例量词的意义，列举在下表的左列。而这些值所对应的对偶量词中可推出的a，p关系相应地列在右边，如下表所示：

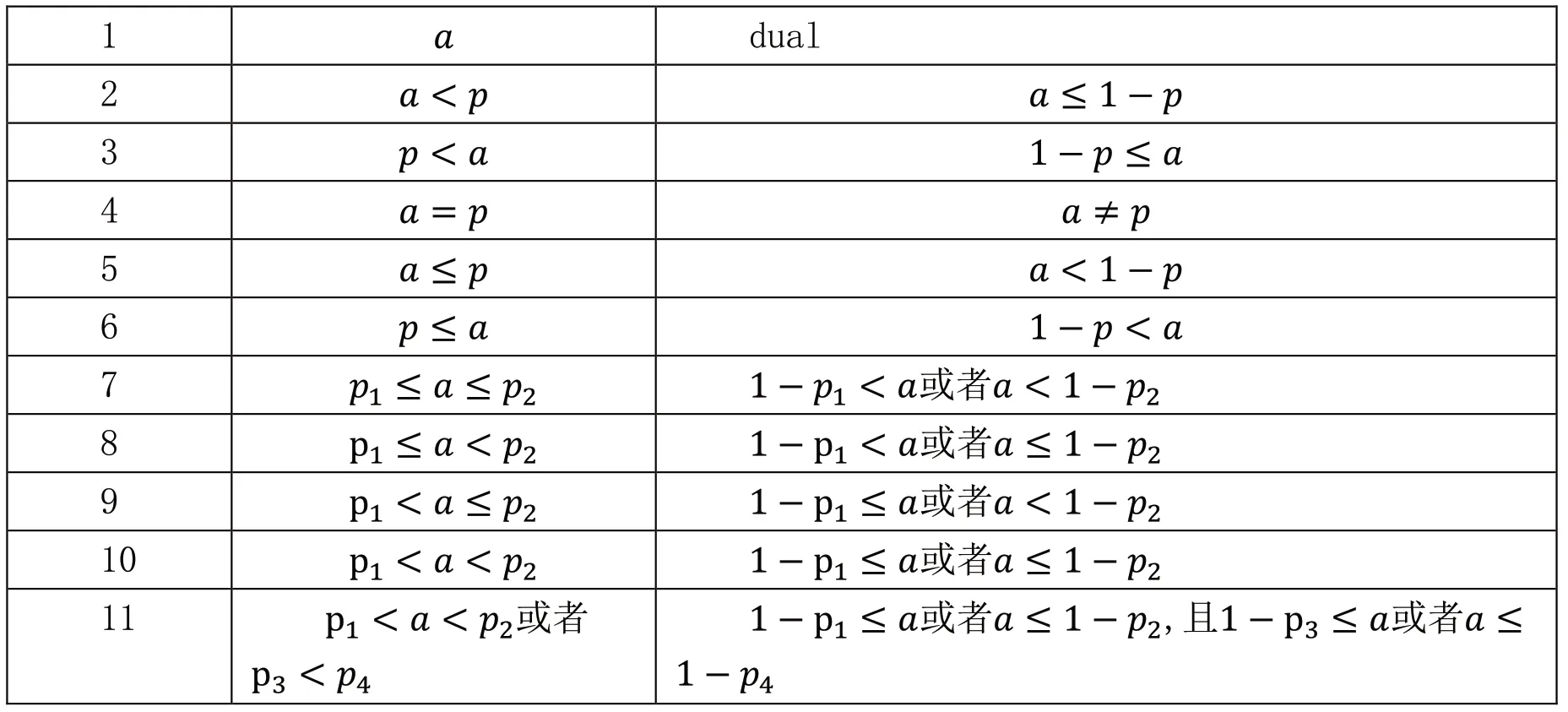
表1 a，p关系表

由此，可以得出关于比例量词对偶运算的一个结论如下：

结论2

设X是有理数区间[0,1]的子集。

对任意比例量词Q，Q满足QM(A,B)⇔∈X等价于QMd(A,B)⇔1-∈Y

（Y是X在[0,1]中的补）。

其中，当X是连续区间时，对应的例子为1-10；X是非连续区间时，对应的例子是11。

证明：

设Q为比例量词，QM(A,B)iff∈X。

则QMd(A,B) iff 并非QM(A,M-B) iff 并非∈Y其中Y=（由A ⊆ M）

在考查比例量词的对偶运算后，我们进一步检测，是否所有的比例量词及其对偶都满足这样的推理模式，即当Q 为比例量词时，推理模式(1)是否有效。

根据我们举例表格，推理模式（1）并非对所有比例量词都有效。例如，第一组量词就不符合该推理模式。

容易得出，要想必然得出存在两种费用都未缴纳的人，必须保证二者在比例上的和超过1，那么二者一定有相交。而根据上述推理模式，我们可知并且从而，因此这两个条件无法必然地得出上述结论。

用同样的思路可以对表格当中的量词一一验证，可知，2 和5 同1 一样，代入这样的推理模式也是不有效的。而4，7，8，9，10，11 由于无法必然地得出二者的和大于1，因此也无法得到有效的推理。可以看出，单说参与推理模式(1)的量词是比例量词则显得过于笼统，因为多数类型的比例量词都是不能有效实现该推理的。

将这种推理模式中的量词归类到比例量词之后，还应该以量词之间的数量关系为保障。这也是我们日常推理当中判断这类推理正确与否时最自然直观的依据。从比例的角度看，两类集合所占比例之和在数量上超过1，就相当于二者的数量和超过了总量，那么必然是存在相交的。那么这种推理模式实际上可用的量词不应当局限于比例量词，只要两个条件当中的量词可以让两个类型的成员数超越总数，就可以得到类似的有效推理。当然，这个推理模式中不仅有数量的要求，还需要保证两个条件当中的量词互为对偶。

要想确保两个条件当中的量词彼此之间的对偶关系，脱离了比例量词这个限制是否可行呢？换句话说，是否存在不是比例量词却适用推理模式（1）的量词呢？根据Keenan（2008），这样的量词不存在。假设在两个条件中，量词表达的不是比例，那就只能是具体的基数n(n ≠0)，即Q(A,B)表达的就是|A ∩ B|=n，那么Qd(A,C)的语义是，|A ∩|≠ n。但是从这两个前提|A ∩ B|=n和|A ∩|≠ n我们无法得知|A ∩ B|+|A ∩ C|与|A|的数量关系。也即，我们通过这两个条件无法看出是B 和是C 的A 的数量是否超过A 的总量，从而无法必然地得出A 中存在同时是B 和C 的成员。由此，我们可以确定，只有比例量词可以满足推理模式(1)。因此，推理模式(1)所需要的数量关系与比例量词的某种性质相关。此外，从以上的例子中我们可以看出，驻留性不能保证量词满足推理模式(1)。

综上，只有比例量词可以满足推理模式(1)，但大多数类型（按数量范围分）的比例量词都不满足该模式。因此，单用比例量词来涵盖整个推理模式当中出现的量词类型是不够的，但比例量词所具备的某些性质在归类当中是必要的。

除了将推理模式(1)中的量词归类为比例量词，Keenan 还在其他推理模式当中使用了比例量词的归类，如Keenan（2008）中提出的中点定理：

定理1（中点定理）

令p,q为分数，使得0≤ p≤ q≤ 1，p+q=1。那么 (BETWEEN p AND q)和(MORE THAN p AND LESS THAN q) 都由¬所固定。

定义7

对分数p 和q 使得0≤p≤q≤1，

(BETWEEN p AND q)(A,B) 当且仅当 A ≠ 0 且

(MORE THAN p AND LESS THAN q)(A,B)当且仅当A ≠0 且p＜＜q。

定义8 量词F由¬所固定，当且仅当F=F¬。

这个定理当中涉及到的量词，对应于上文比例量词表当中的7 和10 类型，除了数值还有进一步的限定：p1+p2=1。对应到表中，可以得到如下关系：

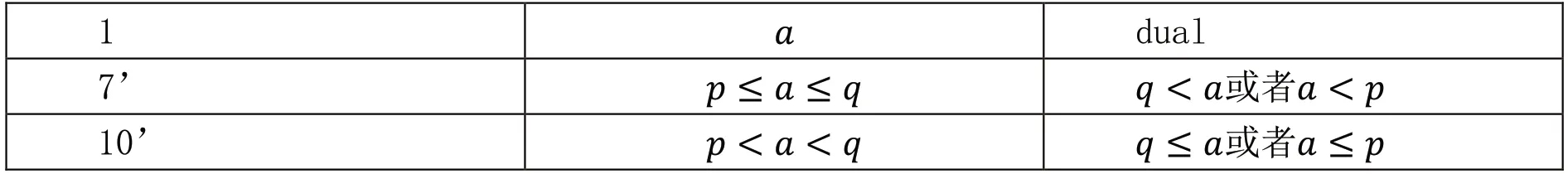
表2 a，p，q关系表

其中，р+q=1。容易看出，这里的量词7’和10’都是它们自身的对偶的否定。即：¬ Q=Qd=¬ Q¬。那么Q=¬¬ Q=¬ Qd=¬¬ Q¬=Q¬，因此Q 被固定，中点定理得证。但同样，Keenan（2008）的这种归类并不能涵盖所有的比例量词类型。但可以确定的是，比例量词特有的表示比例的性质在对偶运算当中可以表示集合间的相交关系，从而确保相应的推理模式有效。

三、单调性的分类方式

如果仅仅给出推理模式(1)，我们可否通过逆推找到其中量词的性质或者满足的条件，从而给出更为精确的归类呢？下面我们尝试逆推满足推理模式(1)的量词具备怎样的性质。

首先，Q不可能是“没有(A,B)”即，若Q(A,B)的语义为“没A是B”那么推理不成立。验证如下：

已知：没有A是B；且并非没有A不是C，则必然没有A同时是B且C。推理显然不成立。

我们对剩下的可能分情况讨论如下：

综上，Q 要使得推理模式(1)有效，须具备如下性质：

性质1

然而，这个性质不容易直接化简。因为我们需要从条件当中出现的作为论元的集合与Q及其对偶量词的关系得出三个集合之间的交集非空的结论，而我们并不知道交集和量词Q之间的具体关系。为了方便化简，我们缩小Q的范围：这样的Q须满足驻留性。这样就可以让Q与交集之间有一定的联系。选择驻留性对锁定Q的范围影响不大，因为自然语言当中不具备驻留性的〈1,1〉类型的量词本身就比较少见，且有争议④。

因此，我们设Q具有驻留性。则性质1 可改写为：

假设Sоmе(A,B ∩ C)不成立，即A ∩B ∩C=Ø。则有A ∩B ⊆。则要想使性质2 成立，我们希望在推理模式(1)的两个条件以及A ∩B ∩C=Ø之间产生矛盾。这个矛盾可以是Q(A,A ∩B)且¬ Q(A,A ∩B)；也可以是Q(A,A ∩)且¬ Q(A,A ∩)。若矛盾是Q(A,A ∩B)且¬ Q(A,A ∩B)，则由Q(A,A ∩)和A ∩B ∩C=Ø可得¬ Q(A,A ∩)，则只需Q 是右单调递增的。同理，若矛盾是¬ Q(A,A ∩)也只需是右单调递增的。因此，Q是右单调递增的可以确保(1)有效。

Barwise 和Cooper 曾经证明了具备右单调性的任何量词都可以满足推理模式（1）。

Westerståhl（2006）认为，满足推理模式(1)的量词就是右单调且驻留的量词。并且给出了证明，这里省略。

而类似于上一节的分析，我们可以从数量的角度归纳Q所必须具备的性质。要保证Sоmе(A,B ∩C)，只需要|A ∩B|+|A ∩C|＞|A|。即只需要。设则Q只需使得x+у＞1即可。但x和у之间理应存在数量关系，因为二者都与Q有关。为了方便测算x与у之间的数量关系，我们设Q(A,B)等价于U=其中，X是有理数区间(0,1]的某个子集，Y是令集合U等价于Q(A,B)成立所需的其他条件的类。Qd(A,C)等价于，其中的是X在区间(0,1]中的补集，Y′是令集合Ud等价于Qd(A,C)成立所需的其他条件的类。也就是说，x的取值范围一定是X，而у的取值范围是{1-b:b ∈}。综上，x和у需要满足的数量关为：x+у＞1，且x ∈X，且у ∈{1-b:b ∈}。其中，条件x ∈X和у ∈{1-b:b ∈}是从推理模式的两个前提得出的，是所有量词都需要满足的条件，而不限于能让推理模式有效的量词。

也就是说，只要量词Q 允许我们从x ∈X和у ∈{1-b:b ∈}得出x+у＞1，那么这个量词就可以令推理模式(1)有效。即只要量词Q允许我们从x ∈X和1-у ∈得出1-у＜x，这个量词就可以令推理模式(1)有效。Q只能令X在数轴上的位置永远在之后。因此Q只能令x的取值范围形如р＜x≤1，р≤ x≤ 1。

若已知Q(A,B)，B ⊆D，设(р,1]为x的取值范围，则有Q(A,B)={x ∈(р,1],Y}，且р＜，若保持条件Y也适用于A,D，则有Q(A,D)。因此，Q是右单调递增的。若条件Y无法适用于A,D，则Y会随着B扩展为D而出现变化。由于Q是驻留的，因此B变为A ∩B不会影响Y的适用性，但二者变为A ∩ D会影响Y的适用性。由于р＜且р＜可知|A ∩ B|=|A ∩ D|，由于B ⊆ D，$A ∩ B ⊆A ∩D。又因为二者基数相同，因此A ∩B=A ∩D。所以Y必然适用于A,D，因此有Q(A,D)。从而Q一定是右单调递增的。

反过来，若Q右单调递增，则在|A ∩B|不断增大的同时，Q(A,B)依然要成立，则对于一个临界点的|A ∩W|值及比它更大的值而言，Q(A,W)都成立。从而我们可知，的取值范围为形如р＜x（如前所述，这里）或р≤x的范围，р为该临界值。这刚好是满足推理模式(1)所需要的Q中x的取值范围。

因此，通过逆推的方法可以发现，满足推理模式(1)的量词刚好是右单调递增的量词。而利用寻找符合推理模式(1)的比例量词时所使用的数量规律逆推量词的性质时，也可以验证量词需具备右单调递增的性质。在数量规律的视角下，单调性可以确保条件x ∈X和у ∈{1-b:b ∈}成立，因此得以实现数量规律。无论如何，单调性的分类方式直观上还是依赖于比例关系。

综合上述分析，可以看出两种分类方式既有区别也有联系，二者作为分类方式也各有利弊。

比例量词的分类方式直观上更符合我们日常判断这个推理模式有效性的思维过程，即通过数量关系得出存在性的判断：两个前提条件只要保证A是B的数量和A是C的数量之和大于A的总量，即可得出存在A同时是B和C。而比例量词可以直观地表示出A分别和B、C之间在数量上的比例关系，因此这种分类方式是最直接也最贴近我们直观推理思路的。但是比例量词按照其范围大小可以分出11 类，而其中大多数类型都不能使该推理模式成立。因此比例量词的分类过于宽泛。但我们可以将其改进为：可以使该模式有效的量词刚好是3 和6 类型的比例量词。

单调性的分类方式更具概括性，且不会夹带大量不符合推理模式的量词：可以使推理模式有效的量词刚好是具备驻留性的右单调的量词。Westerståhl 和Mostowski 虽然给出了证明，但是这种分类方式的直观依据并未得到分析。我们给出了逆推确认量词性质的方法，从数量关系的角度解释了这种分类方式的直观依据、论证了其合理性。首先我们根据推理模式的要求确认了量词需要具备的诸多性质，其次根据量词实际的分布添加了驻留性来缩小量词的范围，接着得出相应于这些性质的数量关系，并化简之。从化简了的数量关系中，我们逆推Q的性质，最终得出量词是右单调递增且驻留的。这里单调性的分类之所以可行的更一般的原因是，单调性的量词本身也是在说明数量范围的关系。比例量词的意义直接地就是一定的数量范围，而右单调递增量词的意义实际上也等价于一定的数量关系，前后两者的数量关系都是论元数量的比例的范围，因此两种分类方式都可以视作在指称一定的数量范围。

但是，如果我们要将自然语言的推理模式(1)迁移到非自然语言的层面，就必须考虑驻留性这个性质对于单纯单调性的干扰。Keenan（2008）反驳单调性分类方式的理由是，自然语言当中满足这个推理模式的具备单调性的量词本身都是比例量词。但是，正是在非自然语言的层面，我们才可能摒弃简单的单调性而选择比例量词的分类方式：我们可以结合两种分类方式的要求，得出：能让推理模式(1)成立的量词，恰好是右单调递增的比例量词，或如前所述，处于特定的数量范围的比例量词。比例量词让我们无需强调驻留性性质，因为比例量词一定是驻留性的。

因此，针对推理模式(1)中量词的分类，比例量词的分类方式可以通过增补比例量词的取值范围来严格化，而单调性的分类方式本质上立足于直观上的数量关系即比例关系。在自然语言的层面，严格化了的比例量词分类方式与右单调递增的分类方式之间是等价的。右单调性的分类方法在自然语言层面看来是更简明的，但在非自然语言的层面则必须增添驻留性的条件。

根据本文中推理模式(1)的量词分类经验，兼考虑量词本身的特性——表示数量关系，遇到自然语言当中量词参与的推理模式，我们可以通过以下途径找出该量词的一般类别或性质：

1.从推理模式出发，确认要使该推理模式成立，量词需要满足哪些条件，这些条件即量词需要满足的性质。

2.从数量角度归纳和化简这些性质，如果遇到障碍，可以寻找新的限制性条件来去掉障碍。例如，在本文的逆推中，化简中的障碍是我们不知道交集和Q之间的关系，采取的办法是增加驻留性这一限定条件。

3.将数量关系之外的其他性质打包成特定的集合。如在本文的逆推中，我们将数量关系之外的性质用集合Y和Y′表示。

4.比照常见的量词性质如同构性，对称性、传递性、单调性等，利用已有的数量关系验证$Q$的性质是否符合这些常见性质或是它们的组合。

利用上述归类思路，我们可以对其他自然语言当中量词参与的推理模式当中的量词做出归类。而反过来，我们也可以从两种类型出发，观察不同类型的比例量词或不同的单调性类型有无专门对应的自然语言推理模式。更进一步我们也可以探索不同的单调性与不同的比例范围之间如何通过量词参与的推理产生关联，从它们之间的关联可否得出一般性的结论。

注释：

①详见类型论（Type Theory）的相关表述。

②例如：这里所有人都是司机。这里的“所有”如果作为谓词，则相当于{人}是{司机}的子集，也就是说，这个谓词表示为：{A×B∈M^2:A⊆B}其中，M指的是人和司机的全体。也就是说，谓词仅限于本论域讨论的对象。而将“所有”视为量词，则该量词可以适用于其他的论域，如“这里所有的苹果都是烂的。这样的用法也更加符合量词的使用情况：不限于具体论域或个体。

③此处的译法参考了张世宁（2010）第34 页。其中阐述了该词的渊源：“根据现有的材料，Barwise 和Cooper是根据所谓驻留（live on）的概念来描述驻留语义性质的。”

④如only_M (A,B)=B⊂A，这里的only不具备驻留性，但是它的量词身份是有争议的，详见Dag Westerståhl等（2006）第139页。