基于切比雪夫距离的支撑点选择算法的并行优化研究
陶顺安 李强 尚小敏 周全 张璁


摘要:
求解切比雪夫距离的支撑点选择算法中,由于计算量较大,如何快速判断支撑点的优劣是一个难以解决的问题,为此,提出一套以切比雪夫距离为目标函数的快速支撑点优选策略。通过并行化分析找出相对独立的计算任务,使用OpenMP对支撑点的选择并行化处理;为降低算法层面的时间复杂度,将切比雪夫距离转化为曼哈顿距离,减少了总体计算量;采用多线程的方法对目标函数值的排序环节进行总体重构,避免了无意义的访存开销。实验结果表明,相比传统方法,支撑点优选算法具有较为明显的加速效果,加速比达到了174.62,并解决了算法的数据依赖问题。
关键词:
切比雪夫距离;支撑点选择;并行计算
中图分类号:
TP338.6
文献标志码:A
度量空间的最大优势在于其高度的普遍适用性,用户只需提供距离函数就可以进行相似性搜索。然而,度量空间的优势也是其劣势,数据被抽象成度量空间中的点,虽然提高了通用性,但同时损失了坐标信息,唯一可用的信息就是距离。由于没有坐标,许多数学方法不能直接使用。为此,通常先找出一些参考点(也称支撑点,Pivot),然后将数据到此参考点的距离作为坐标。支撑点的好坏对于度量空间数据管理分析的性能发挥着关键性的影响[1],支撑点的选取可以从目标函数和选择算法两个方面进行研究。常用的目标函数是均值目标函数[2-4],Bustos[5]研究了k维支撑点空间中的距离对的均值和方差,以均值作为目标函数值,选出均值最大时所对应的数据作为支撑点,但没有考虑查询半径对排除效果的影响。常用的支撑点选择算法[6-7]包括最远优先遍历(Farthest First Traversal,FFT)[8]和Incremental[9-10]。FFT可以在线性时间内选出数据拐角的点,并且性能有一定的保证,但是,实验表明最好的支撑点往往不是拐角的点,因而FFT很难选出最优点。Incremental是一种增量式选择支撑点的算法,也能够快速地选出支撑点,但存在着局部最优的问题,即以最优目标函数值依次选出的两个支撑点组合在一起,不一定是性能最优的支撑点组合。采用暴力枚举法和快速支撑点选择穷举算法选取支撑点时,通过MPI通信在节点间传输数据,在节点内采用多进程并行的计算方式,以得到最优和最劣支撑点的分布情况,但并没有解决算法本身的数据依赖问题[11-12]。本文改进了支撑点选择的穷举算法,提出一套支撑点优选策略,以任意两点的重建坐标间的切比雪夫距离为目标函数,选出最优和最差的支撑点组合,并对此算法进行线程级并行优化[13],在保证准确性的前提下解决了数据依赖问题,使算法得到了显著的加速。
1 基于切比雪夫距离的支撑点选择算法分析
1.1 算法设计
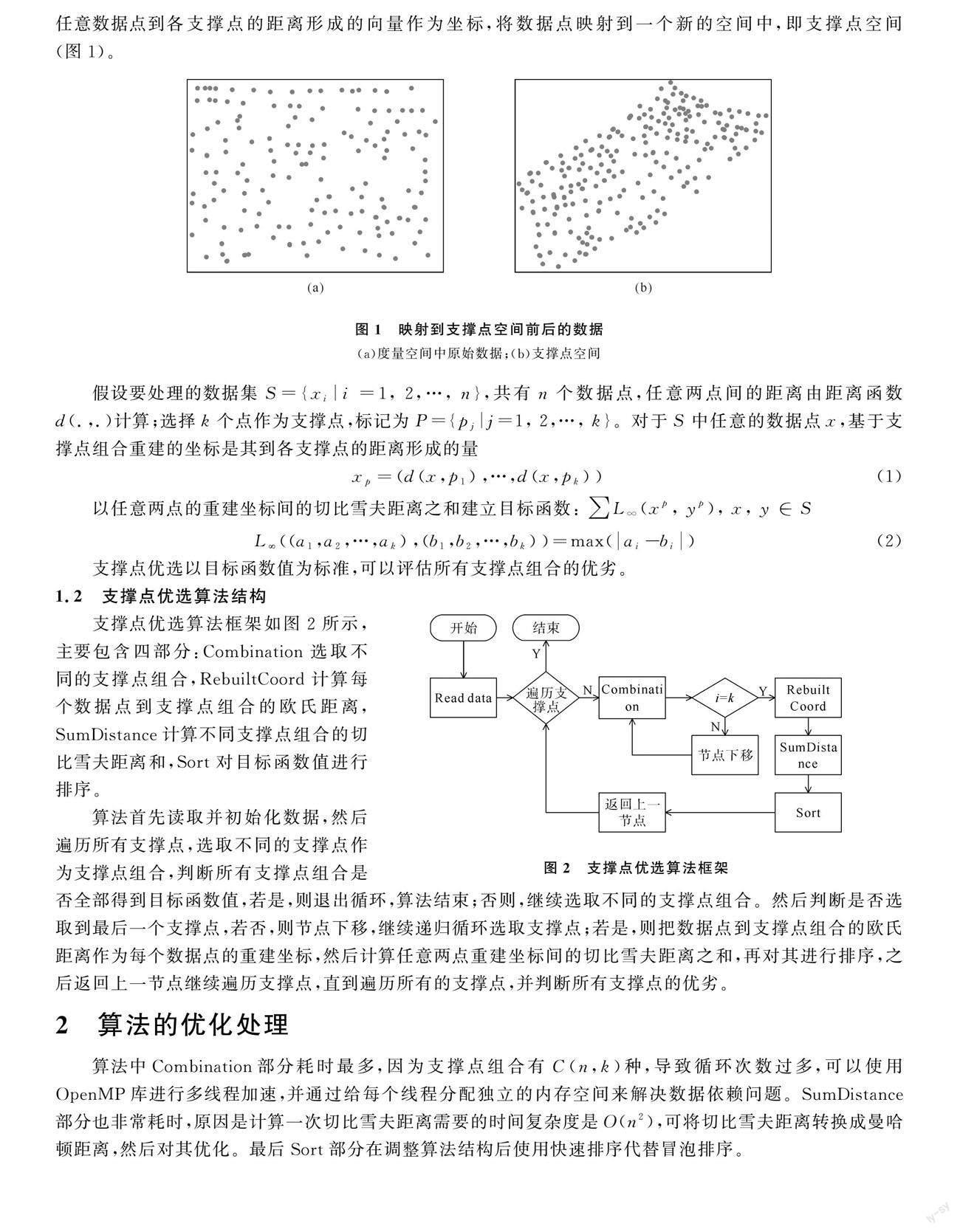
在度量空间中,数据点没有坐标值,距离是唯一可用的信息,但一些基于数学工具的数据处理方式难以直接利用。为便于处理和分析数据点,提出了支撑点空间的概念[14],从数据集中选取一些点作为支撑点,将任意数据点到各支撑点的距离形成的向量作为坐标,将数据点映射到一个新的空间中,即支撑点空间(图1)。
假设要处理的数据集S={xi|i =1, 2,…, n},共有n个数据点,任意两点间的距离由距离函数d(.,.)计算;选择k个点作为支撑点,标记为P={pj|j=1, 2,…, k}。对于S中任意的数据点x,基于支撑点组合重建的坐标是其到各支撑点的距离形成的量
支撑点优选以目标函数值为标准,可以评估所有支撑点组合的优劣。
1.2 支撑点优选算法结构
支撑点优选算法框架如图2所示,主要包含四部分:Combination选取不同的支撑点组合,RebuiltCoord计算每个数据点到支撑点组合的欧氏距离,SumDistance计算不同支撑点组合的切比雪夫距离和,Sort对目标函数值进行排序。
算法首先读取并初始化数据,然后遍历所有支撑点,选取不同的支撑点作为支撑点组合,判断所有支撑点组合是否全部得到目标函数值,若是,则退出循环,算法结束;否则,继续选取不同的支撑点组合。然后判断是否选取到最后一个支撑点,若否,则节点下移,继续递归循环选取支撑点;若是,则把数据点到支撑点组合的欧氏距离作为每个数据点的重建坐标,然后计算任意两点重建坐标间的切比雪夫距离之和,再对其进行排序,之后返回上一节点继续遍历支撑点,直到遍历所有的支撑点,并判断所有支撐点的优劣。
2 算法的优化处理
算法中Combination部分耗时最多,因为支撑点组合有C(n,k)种,导致循环次数过多,可以使用OpenMP库进行多线程加速,并通过给每个线程分配独立的内存空间来解决数据依赖问题。SumDistance部分也非常耗时,原因是计算一次切比雪夫距离需要的时间复杂度是O(n2),可将切比雪夫距离转换成曼哈顿距离,然后对其优化。最后Sort部分在调整算法结构后使用快速排序代替冒泡排序。
2.1 OpenMP并行优化
OpenMP(Open Multi-Processing)是一种用于共享内存多处理器计算机的应用程序编程接口(API),可提供一系列的指令集、库例程和环境变量等,能为程序员提供方便灵活的编程方式,实现多线程、共享内存计算中的并行运算。在支撑点优选算法中,Combination选取最后一个支撑点时,剩下的数据点之间是相互独立的,因此计算结果不会受到其他数据点的影响。这种独立性能够更高效地处理大量数据,并可将计算任务分配给多个处理器以加快处理速度。在Combination部分,使用OpenMP指令#pragma omp parallel for可以让不同的线程同时处理不同的支撑点组合,从而加快计算速度。同时,由于每个线程都独立工作,可以避免数据竞争的情况。使用多线程计算时,为了解决数据依赖问题并保证计算结果的正确性和稳定性,将不同线程的计算结果存储到不同的内存空间中。这样,不同线程之间不会出现数据互相干扰或覆盖的情况,而且每个线程计算完成后,结果也能够得以正确保存,供其他线程继续使用。
2.2 SumDistance优化
本文采用了将切比雪夫距离转换为曼哈顿距离的优化方法。设平面内存在两点,坐标为(x1,y1),(x2,y2),则切比雪夫距离为max{|x1-x2|, |y1-y2|},即两点横纵坐标差的最大值,曼哈顿距离为|x1-x2|+|y1-y2|,即两点横、纵坐标差的绝对值之和。切比雪夫距离和曼哈顿距离可以互相转化,在笛卡尔坐标系中,用边长为2的正方形表示切比雪夫距离(图3(a)),用边长为 2的正方形表示曼哈顿距离(图3(b))。
对比图3(a)和(b),将点(x,y)的坐标变为(x+y,x-y)后,原坐标系的曼哈顿距离等于新坐标系的切比雪夫距离。将点(x,y)的坐标变为(0.5(x+y),0.5(x-y))后,原坐标系的切比雪夫距离等于新坐标系的曼哈顿距离。由于切比雪夫距离在计算时需要取最大值,所以不能直接优化,对于一个点,计算其他点到该点距离的复杂度为O(n),计算任意两点的切比雪夫距离和时,复杂度为O(n2)。而曼哈顿距离只有求和以及取绝对值两种运算,把坐标排序后可以去掉绝对值的影响,进而用前缀和优化,可以把复杂度降为O(1),计算任意两点的曼哈顿距离和时,复杂度为O(n)。
使用一个数组存n个点对第一个支撑点的距离,然后对数组从小到大快速排序,以此去掉绝对值的影响。xi代表第i个数据点(1≤i≤n),前缀和res表示第i个数据点到其他数据点距离之和,简化为
res=res+xi-x0+xi-x1+xi-x2+xi-x3+…+xi-xi-1(3)
res=res+xi*i-x0+x1+x2+…+xi-1(4)
res=res+xi*i-Si-1(5)
同理,任意两个点y坐标的曼哈顿距离一样处理。|x1-x2|+|y1-y2|即为曼哈顿距离,对所有点的曼哈顿距离优化求和即为原坐标系的切比雪夫距离之和。由于对所有点进行快速排序的时间复杂度为O(nlog n),故求切比雪夫距离和的时间复杂度由O(n2)优化到O(nlog n)。
2.3 Sort优化
对于串行算法,每得到一个目标函数值,就对其进行冒泡排序,以得到对应支撑点组合的排序位置。由于总共有C(n,k)种支撑点组合,获得C(n,k)个目标函数值,因此需要C(n,k)次冒泡排序,时间复杂度为O(n2)。因为每次冒泡排序并不能确定目标函数值的最终位置,所以出现反复冒泡交换产生的无意义访存开销,效率太低。
对于Sort部分,本文使用一个数组把每种支撑点组合所得到的目标函数值存储起来,待所有支撑点组合遍历结束,数组中将存储所有的目标函数值,然后对这些目标函数值快速排序。
修改后的并行算法使用多线程计算所有支撑点组合的目标函数值,并将其存储在一个数组中。不同的线程需要将不同的目标函数值存储在不同的位置,因此需要给每个线程开辟一个私有空间存储数据,避免产生数据冲突、数据覆盖等问题。经过推理,以k=2为例,当数组以C(n,k)-C(n-i,k)+C(n-i-1,k-1)-C(n-j,k-1)(i,j为选取的两个支撑点)为索引下标时,每个线程都可以得到数组的一段空间来存储各自的目标函数值。最后对这个数组快速排序,仅需排序一次,时间复杂度为O(nlog n)。当使用64个线程存储数据时,各线程的存储位置如图4所示。
3 实验环境与结果
3.1 实验环境设置
硬件环境,CPU:AMD EPYC 7452 32-Core Processor,双节点,每节点双socket,每socket 32核心;软件环境,OS:CentOS Linux release 7.9.2009;GCC compiler:GCC-8.1.0;实验规模,数据点n=500,支撑点k=2。
3.2 消融研究
3.2.1 加入OpenMP的多线程优化对比 经过实验测试,OpenMP对Combination的加速效果较为明显。算法的总运行时间随着线程数的增加而逐步减少,在线程数为64时总运行时间最小,为1 191 ms,如图5(a)所示。随着线程数的增加,加速比最高达到了37.53,并行效率为58.6%(图5(b))。
3.2.2 Sort部分优化对比 经过测试,在优化前,Sort时间为272 ms,而優化后仅需要14 ms,加速比高达19.43,如图6(a)所示。在使用64线程并行计算的基础上,算法总运行时间从最初的1 191 ms缩短至571 ms,加速比从37.53提升至78.29(图6(b))。
3.2.3 SumDistance部分优化对比 在64个线程的并行环境下,对SumDistance部分从根本上进行优化,算法具体良好的加速趋向,SumDistance时间由416 ms变为了117 ms,加速比达到了3.56(图7(a));算法总的运行时间最低达到了256 ms,加速比从78.29增大到了174.62,如图7(b)所示。
4 结论
本文主要调整了支撑点优选算法的SumDistance和Sort部分结构,使时间复杂度从O(n2)降低到O(nlog n)。针对算法中的主要瓶颈Combination等进行了线程级并行优化,使算法得到了较大的加速。接下来将在超级计算机上进行上百节点的测试,并使用cpu与gpu(或加速器)的异构众核架构进行并行加速。
参考文献
[1]李兴亮,毛睿.基于近期最远遍历的支撑点选择[J].南京大学学报(自然科学),2017,53(3):483-496.
[2]NAVARRO G. Analyzing metric space indexes: What for?[C]// 2nd International Workshop on Similarity Search and Applications. Prague, 2009: 3-10.
[3]VENKATESWARAN J, KAHVECI T, JERMAINE C, et al. Reference-based indexing for metric spaces with costly distance measures[J]. The VLDB Journal, 2008, 17(5): 1231-1251.
[4]CHEN L, GAO Y J, LI X H, et al. Efficient metric indexing for similarity search[C]// 31st International Conference on Data Engineering. Seoul, 2015: 591-602.
[5]BUSTOS B, NAVARRO G, CHAVEZ E. Pivot selection techniques for proximity searching in metric spaces[J]. Pattern Recognition Letters, 2003, 24(14): 2357-2366.
[6]ZHU Y F, CHEN L, GAO Y J, et al. Pivot selection algorithms in metric spaces: a survey and experimental study[J]. The VLDB Journal, 2022, 31(1): 1-25.
[7]JETPJPATTANAPONG D, SRIJUNTONGSIRI G. A new pivot selection algorithm for symmetric indefinite factorization arising in quadratic programming with block constraint matrices[J]. Chiang Mai Journal of Science, 2018, 45(2): 1181-1193.
[8]BERMAN A, SHAPIRO L G. Selecting good keys for triangle-inequality-based pruning algorithms[C]// IEEE International Workshop on Content-Based Access of Image and Video Database.Bombay, 1998: 12-19.
[9]YANG K Y, DING X, ZHANG Y L, et al. Distributed similarity queries in metric spaces[J]. Data Science and Engineering, 2019, 4(2): 93-108.
[10] MAO R, ZHANG P H, LI X L, et al. Pivot selection for metric-space indexing[J]. International Journal of Machine Learning and Cybernetics, 2016, 7(2): 311-323.
[11] 李兴亮. 度量空间索引支撑点选择问题研究[D].合肥:中国科学技术大学,2017.
[12] 胡梓良. 度量空间支撑点选择穷举算法优化及并行化研究[D]. 深圳:深圳大学, 2019.
[13] 尚小敏,李强,齐永孟,等.SLIC算法的线程级并行优化研究与实现[J].青岛大学学报(自然科学版),2022,35(4):20-25+32.
[14] MAO R, MIRANKER W L, MIRANKER D P. Pivot selection: Dimension reduction for distance-based indexing[J]. Journal of Discrete Algorithms, 2012, 13: 32-46.
Research of Parallel Optimization of Pivot Selection Algorithm
Based on Chebyshev Distance
TAO Shun-an,LI Qiang,SHANG Xiao-min,ZHOU Quan,ZHANG Cong
(College of Computer Science and Technology, Qingdao University, Qingdao 266071, China)
Abstract:
In the pivot selection algorithm for solving Chebyshev distance, how to quickly determine the strength and weakness of pivot has always been a difficult problem to solve due to the large amount of calculation. Therefore, a set of fast pivot optimization strategy with Chebyshev distance as the objective function was proposed. Through parallelized analysis, relatively independent computing tasks were found, and OpenMP was used to parallelize the selection of pivot. In order to reduce the time complexity at the algorithm level, the Chebyshev distance was converted into the Manhattan distance, which reduces the overall calculation amount. The multi-threaded method was used to reconstruct the ordering link of the objective function value as a whole, which avoids the meaningless memory fetching overhead. The experimental results show that the pivot optimization algorithm is a more obvious acceleration effect than the traditional method, and the speedup reaches 174.62, and the data dependence problem of the algorithm is solved.
Keywords:
Chebyshev distance; pivot selection; parallel computing
收稿日期:2023-03-07
基金項目:
山东省自然科学基金面上项目(批准号:ZR201910310143)资助。
通信作者:
李强,男,博士,讲师,主要研究方向高性能计算。E-mail: lq.sxt@163.com

