河流生态系统中两个相互作用种群的空间模式的形成①

喻凤斯， 尹甜， 黄启华

西南大学 数学与统计学院，重庆 400715

大量水生生物(如浮游生物、藻类、溪流昆虫等)生活在河流、溪流等具有单向水流的生态系统中.为何生物种群在受到从上游向下游单向水流不断冲刷的情形下能够生存?这是河流生态理论中一个重要的被称为“漂移悖论”(driftparadox)的科学问题.为了解释该科学问题,多位科学工作者建立并研究了一系列包括对流和扩散过程的反应-扩散-对流方程模型和积分-微分方程模型[1-7].这些模型描述了河流种群的时空演变过程,其长期动力学行为(持久性或灭绝)通过多种数学理论和工具被深入研究,例如一致持久性、零解的稳定(不稳定)性、正稳态解的存在性和稳定性、临界区域长度、行波解和渐进传播速度等.基于上诉文献中的单个种群模型,许多研究者建立了两个相互作用的河流种群模型,着重研究了水流的速度、种群的扩散系数等因素如何影响种群的共存(排斥),例如: 文献[8-10]研究了两个竞争种群的模型; 文献[11]研究了河流生态系统中的捕食-食饵种群的模型.这些模型具有以下一般的形式:

(1)

其中:u(x,t),v(x,t)表示位置在x处、时间在t处两物种的密度;di(i=1,2)是扩散常数,qi(i=1,2)是对流系数(即水流速度),f(u,v)与g(u,v)为反应函数．

当q1=q2=0时,系统(1)变成经典的两个相互作用种群的反应-扩散方程模型.反应-扩散方程模型中由扩散导致的常数稳态解的不稳定性称为Turing不稳定性．

本节的主要目的是研究反应-扩散-对流模型(1)中的单向水流(即对流项)对斑图动力学的影响(q1=q2=q).为此,我们考虑如下长度为L的河流中两个相互作用种群的动力学模型:

(2)

其中的Neuman边界条件表示河流上游有随着河流自然流入的种群,河流下游随着时间流逝有被河水带走的种群．

1 q=0时的Turing不稳定

本节讨论没有水流的影响,及q=0的情形下,系统(2)的Turing不稳定性．

假设(u*,v*)是系统(2)的常数稳态解,将系统(2)在(u*,v*)处线性化,令φ=u-u*,φ=v-v*,则有

(3)

其中f1=fu(u*,v*),f2=fv(u*,v*),g1=gu(u*,v*),g2=gv(u*,v*).用矩阵表示为

Ψt=DΔΨ-QΨ+JΨ

(4)

其中

在一维Neuman边界条件情形下,系统(4)解的形式为

(5)

(6)

其中

(7)

(8)

在(5)式中ω=ω(k)是决定稳态(u*,v*)稳定性的特征值.对于k=0,(6)式的两个根满足

(9)

假设

f1+g2<0,f1g2-f2g1>0

(10)

这意味着稳态(u*,v*)在没有空间作用的情况下是线性稳定的.现在对于k>0,(6)式的两个根满足

(11)

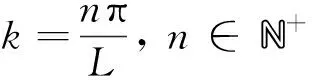
d1g2+d2f1>0

(12)

和

(d1g2+d2f1)2-4d1d2|J|>0

(13)

(14)

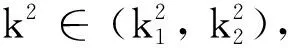
(15)

事实上不等式(15)是不等式(13)的充分条件.通过上面讨论得出如下定理．

定理1假设(10),(12),(15)式同时成立的情况下,系统(2)的空间齐次稳态解(u*,v*)会发生Turing不稳定．

2 水流(q>0)对Turing不稳定的影响

接下来考虑在发生Turing不稳定后,加入对流的情况,即系统(2)中q>0．

这时系统(4)解的形式变为

同上讨论,(6)式变成:

(16)

其中

Mk的迹和行列式值为:

(17)

aq4+bq2+c=0

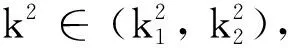
(18)

3 一个捕食-食饵模型的斑图动力学

标准的Lotka-Volterra捕食-食饵模型假设单位捕食率只依赖于食饵的数量.但在大多数情况下,特别是当捕食者需要花更多时间去寻找食物时,更适合的捕食-食饵系统应建立在所谓的比例依赖性理论上[12].也就是说,单位捕食者增长率应该是食饵与捕食者比值的函数.文献[13-14]讨论了扩散驱动捕食-食饵模型产生空间结构的一些条件.近年来一些研究者研究了比例依赖(即反应项具有收获率)的捕食-食饵模型[15-16].我们考虑生活在河流生态系统中的捕食和食饵种群的相互作用,研究以下具有捕食者收获率的反应-扩散-对流比例依赖捕食-食饵模型的时空模型

(19)

其中:u(x,t),u(v,t)分别代表食饵与捕食者的密度,r表示食饵的内在增长率,K代表环境容纳量,c代表捕获率,c1代表转化系数,m代表半捕获饱和常数,e代表捕食者死亡率,h代表收获率.为了方便,对系统(19)进行无量纲化:

仍记变量为u,v,x,t,q,则系统(19)可以写成

(20)

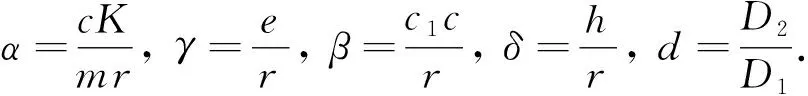
系统(20)对应的常微分系统为

(21)

模型(21)在E*的Jacobian矩阵为

其中:

对应的特征多项式为

P(λ)=λ2-(f1+g2)λ+f1g2-f2g1

对于Jacobian矩阵J(u*,v*)有如下结论．

引理11) 如果(H1)成立,则f1g2-f2g1>0．

2) 如果

(H2)αβ2+β(γ+δ)2<α(γ+δ)2+(γ+δ+1)β2

成立,则f1+g2<0．

3) 如果

(H3)αβ2+β(γ+δ)2>α(γ+δ)2+(γ+δ+1)β2

成立,则f1+g2>0．

通过对Jacobian矩阵J的讨论,可得出如下结论．

定理3假设(H1)成立.如果(H2)成立,系统(21)的唯一正平衡点E*是局部渐进稳定的; 但如果(H3)成立,系统(21)的唯一正平衡点E*是不稳定的．

系统(21)正平衡点E*也是系统(20)的空间齐次稳态解.由定理1知,发生Turing不稳定当且仅当

(22)

下面利用Matlab对上诉模型进行数值模拟,以此来验证以上理论分析的结果．

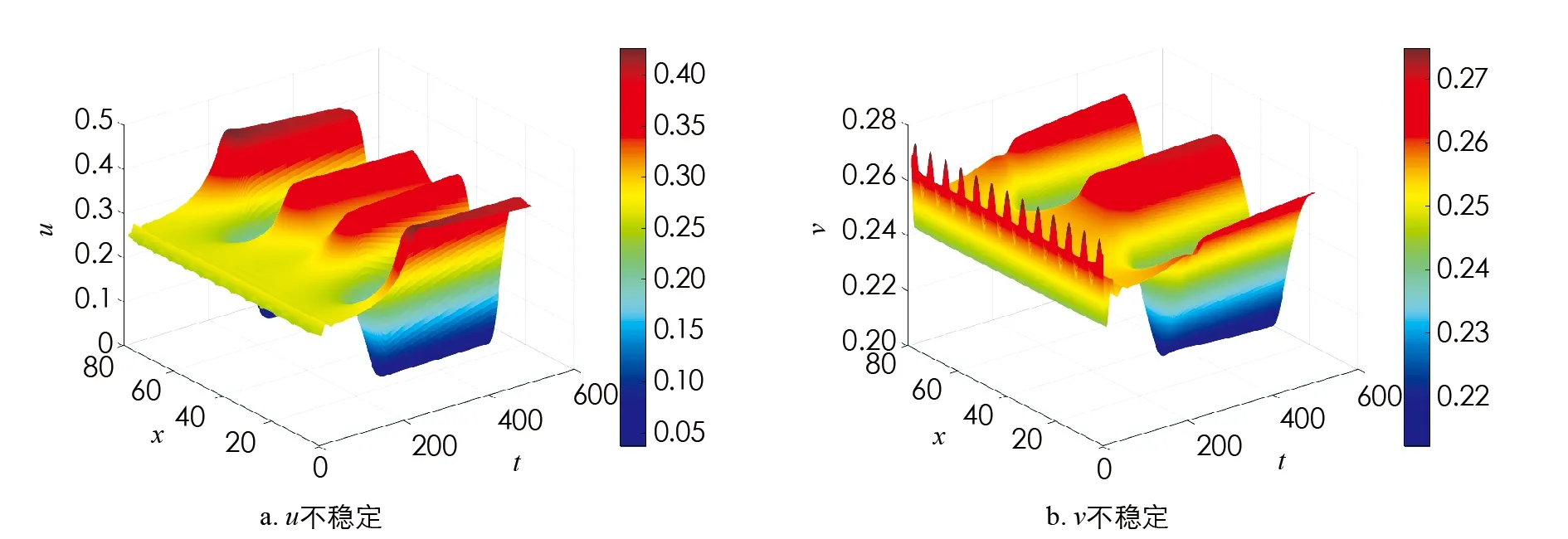
图2 模型(20)正常数稳态解的Turing不稳定性

图3 加入q后模型(20)正常数稳态解的Turing不稳定性

图4 模型(20)重新稳定后的正常数稳态解

4 讨论

我们利用反应―扩散―对流方程来描述河流生态系统中的捕食者与食饵的相互作用,研究了在河流长度一定的条件下发生Turing不稳定性的一些必要条件,还研究了对流项对Turing不稳定的影响.发现存在一个对流系数临界值,当对流系数大于临界值时会使发生Turing不稳定的常数平衡解重新稳定,但当对流系数小于临界值时,加入对流项对Turing不稳定性不产生影响.但本文研究的情况比较特殊,本文中的边界条件是一维Neuman边界条件,还假设了对流项系数相等.如果对流项系数不等,那么河流长度无限长等情况都有待进一步研究．