Reverse-time type nonlocal Sasa-Satsuma equation and its soliton solutions

Xue-Wei Yanand Yong Chen

School of Mathematics,Harbin Institute of Technology,Harbin,150001,China

Abstract

In this work,we study the Riemann-Hilbert problem and the soliton solutions for a nonlocal Sasa-Satsuma equation with reverse-time type,which is deduced from a reduction of the coupled Sasa-Satsuma system.Since the coupled Sasa-Satsuma system can describe the dynamic behaviors of two ultrashort pulse envelopes in birefringent fiber,our equation presented here has great physical applications.The classification of soliton solutions is studied in this nonlocal model by considering an inverse scattering transform to the Riemann-Hilbert problem.Simultaneously,we find that the symmetry relations of discrete data in the special nonlocal model are very complicated.Especially,the eigenvectors in the scattering data are determined by the number and location of eigenvalues.Furthermore,multi-soliton solutions are not a simple nonlinear superposition of multiple single-solitons.They exhibit some novel dynamics of solitons,including meandering and sudden position shifts.Also,they have the bound state of multi-soliton entanglement and its interaction with solitons.

Keywords: nonlocal Sasa-Satsuma equation,Riemann-Hilbert problem,soliton solution

1.Introduction

The nonlinear Schrödinger(NLS)equation plays a key role in mathematical physics,especially in describing soliton propagation in optical fibers.However,the NLS equation only includes the self-phase modulation (SPM) effect and group velocity dispersion(GVD)[1,2].Apart from these two terms,there are intensive and short light pulses with widths less than 100 femtoseconds in nonlinear optics,which are also considered in linear and nonlinear effects,such as third-order dispersion (TOD),self-steepening (SS),and stimulated Raman scattering (SRS) [3-7].To describe the dynamics of ultrashort pulses,a higher order NLS equation also called Sasa-Satsuma equation was proposed in [8-11].When one considers the simultaneous propagation of two ultrashort pulses in birefringent or two-mode fiber,coupled Sasa-Satsuma (CSS) equation included TOD,SS,and SRS was proposed in [12-15],and has the form of

which converts to another form [15]

under the gauge,Galilean and scale transformations

The Riemann-Hilbert method is the modern version of the inverse scattering transform.Recently,a lot of interesting and meaningful results have been obtained by applying the Riemann-Hilbert method.For instance,Wang et al studied the general coupled NLS equation and reported the collision dynamics of multi-soliton,recursion operator and conservation laws[16].Shepelsky studied the Dullin-Gottwald-Holm equation with the Cauchy problem,using Riemann-Hilbert approach.Moreover,smooth and non-smooth cuspon solutions have been researched in [17].Recently,Ma used the inverse scattering transform to study several types of reversespacetime nonlinear integrable equations and obtained various interesting results [18-20].Besides,other important work has been reported in [21-26].In recent years,the method has also been developed to study the asymptotic behaviors of solutions and initial boundary value problems for some integrable equations and has obtained some important results [27-38].

In this work,we focus on a physically meaningful nonlocal Sasa-Satsuma equation of reverse time type [39,40]

under the constraint

in equation (2),where* denotes complex conjugation.The nonlinear induced potential (|u|2+|u(x,-t)|2) is real and symmetric in t.Equation (4) is derived from a special reduction of another form of the CSS equation,i.e.(2).equations (2) and (4) are two equivalent coupled systems,under constraint (5).By considering the derivation of this nonlocal equation,we can obtain the clear physical interpretation of its solutions.That is to say,equation(4)describes the solutions of the CSS equation,if considering the initial value conditions v(x,0)=u*(x,0).Based on this,u(x,t) is determined by equation (4),and v(x,t) is given by

v(x,t)=u*(x,-t).For the CSS equation,Tian et al used Darboux transformation to study Dark-bright solitons and semirational rogue wave solutions [41].Based on the nonlinear steepest descent approach,the long-time asymptotic behavior of solutions has been reported in [40].Even though the CSS equation has been studied and generated much important work [42-44],to the best of our knowledge,its solutions with special initial solutions v(x,0)=u*(x,0) have not received much attention.

There is another form of the reverse space-time nonlocal SS equation proposed in[45].Its periodic solutions,and some localized solutions,such as dark soliton solutions,W-shaped soliton solutions,M-shaped soliton solutions and breather soliton solutions have been investigated by using the binary Darboux transformation method.Various solutions u(x,t)are determined by the nonlocal SS equation,the results of which,provide an important channel for the study of these solutions in the framework of this nonlocal equation.Due to the integrability of the nonlocal SS equation,it is natural to think of seeking its soliton solutions,which also correspond to the solutions of the CSS equation.Thus,we study the multisoliton solutions of the nonlocal SS equation in the framework of the Riemann-Hilbert problem by using the inverse scattering transform.Our work is developing the Riemann-Hilbert approach to derive the multi-soliton solutions of the nonlocal SS equation,which has not been considered by others.Our goal in this paper is to explain the transmission mechanism of ultrashort pulse solitons in birefringent fiber by constructing the multi-soliton solutions for the nonlocal SS equation.

The paper is organized as follows.In section 2,using a matrix transform derives an equivalent spectral problem,which can be used to obtain a special Riemann-Hilbert problem.In section 3,under reflection-less by using inverse scattering transform to the Riemann-Hilbert problem,some continuous and discrete scattering data can be obtained,and as a result,the general solutions of the Riemann-Hilbert problem can also be obtained.In section 4,the multi-soliton solutions for the nonlocal SS equation can be derived.Finally,some conclusions are presented.

2.Riemann-Hilbert problem

In this section,we consider the direct and inverse scattering problems of equation(4).Equation(4)admits the Lax spectral problem

and

where † denotes Hermitian conjugation,and T is transpose.Using a transformation

we derive the equivalent matrix spectral problem

In order to obtain direct scattering problem,let J±be the Jost solutions for (9) and satisfy the asymptotic conditions

Solving the space evolution (9) we obtain the Volterra integral equations

If the right sides of the Volterra integral equations (12) are convergent,then J±exist analytical continuations off the real axisλ∊R.In addition,J±have a relation that

Suppose that J±have the block forms

whereJ±(j),(1≤j≤5)are jth columns of J±.Then the matrix solution

is analytic in upper half-planeC+and continuous in closed upper half-plane,where σ(1)=diag(I4×4,0),σ(2)=diag(04×4,1).The matrix solution

is analytic in lower half-plane-C and continuous in closed lower half-plane.

Moreover,the Volterra integral equations indicate that

Because of the traceless U,using the Volterra integral equations,it follows

Next,we consider the analytic counterpart of Ψ+in+C from the adjoint spectral problem

with

We also find that the adjoint matrix solution

is analytic in-C.The matrix solution

is analytic inC+.Similar to the asymptotic conditions (17),we also have

Thus,the matrix functions Ψ+and Ψ-have been derived.They are analytic in+C and-C,and are continuous inand,respectively.

We further seek that a relation between Ψ+and Ψ-on real axis satisfies

where

Equation (26) is the matrix Riemann-Hilbert problem for the nonlocal SS equation.According to the asymptotic properties in (17) and (25),we obtain the canonical normalization conditions

for the Riemann-Hilbert problem (26).

To derive a direct scattering problem,we use the t-derivative of(13)and the vanishing conditions of the potential u,when t→∞.It is not hard to get

from which we derive the time-dependent scattering datum

Besides,other scattering datum are independent of t.

3.Inverse scattering transform

In what follows,according to the definitions ofdet (ψ+) and det (ψ-),one yields

This shows thatdet (ψ)+anddet (ψ)-have the same zero points ass55,,respectively.Equation (21) satisfies

According to equation (13),we can obtain

where the entries of S,S-1satisfy

Moreover,we find U satisfies the two symmetry relations

with

which arrives at

Actually,S satisfies ΔS(-λ*)Δ=S(λ),which follows that

Theorem 3.1.det (ψ±) have three types of zero structures as follows.

respectively.

According to case (I),we know thatdet (ψ+) has 2N1zeros λj,(1 ≤j ≤2N1) inC+,whereλN1+l=-λ*l,(1≤l≤N1).Then the zeros ofdet (ψ-) are conjugated to the zeros ofdet (ψ+).The symmetry (41) gives the relation of det (ψ+) at (x,-t,-λ*) and (x,t,λ).The symmetry (42)indicates thatdet (ψ+) at (x,t,λ*) equates todet (ψ-) at (x,t,λ).Thus,based on (43) andλN1+l=-λ*l,we have the symmetries

This indicates that one only needs to solve vj,(1 ≤j ≤N1),such that all vectors vjandcan be obtained.Thus by taking the x,t-derivatives of the first expression in equation(43)and integrating it,we have

and

whereθj(x,t)=iλjx+4iλ3jt,λj∊C+,λjR≠0,and vj,0are column vectors independent of x,t.

Next,we introduce the matrices

whereM=(mkj)2N1×2N1is an invertible matrix,and

Using Φ±(λ),we regulate the Riemann-Hilbert problem(26)to a regular one.Then,it satisfies

where Ω±(λ) satisfy

with

Ifs5j,,(1≤j≤4)are nonzero constants,i.e.the Riemann-Hilbert problem (26) contains reflection data,precise solutions can not be obtained,due to the imprecisely solvable integrable equations (51) w.r.t.Ω±.Hence,in order to construct explicit soliton solutions,the Riemann-Hilbert problem is needed to be reconsidered under reflection-less.Calculating the Riemann-Hilbert problem (26),one has the following solutions

whereM=(mkj)2N1×2N1is an invertible matrix with

For case(II),det (ψ+) has N2zerosλj∊ iR,(1≤j≤N2)in C+.Then the zeros ofdet (ψ)-are conjugated to the zeros of det (ψ+).Similar to case(I),the vectorsvj,,(1≤j≤N2)arrive at

where θj(x,t),(1 ≤j ≤N2) are the same as (46)-(47).Thus,under the case of reflection-less,the general solutions for the Riemann-Hilbert problem (26) are given by

where the elements mkjof M are the same as (55),besides 1 ≤j ≤N2.

For case (III),as a combination of the first two cases,its discrete scattering datum has the following results

and

where θj(x,t),(1 ≤j ≤2N1+N2) are the same as (46)-(47).Without loss of generality,the general solutions of the Riemann-Hilbert problem (26) are

where the forms of the elements of M are the same as (55),besides 1 ≤j ≤2N1+N2.

Now,we consider the asymptotic expansion of Ψ+(λ)

which can be used to reconstruct the potential u.Substituting(63) into (9),we have

which implies that,

According to (53),(57) and (63),ψ+(1)respectively corresponds to the following expressions

4.Soliton solutions for the Riemann-Hilbert problem

According to the three types of zero structures ofdet (ψ)±presented in theorem 3.1,we derive the multi-soliton solutions for the nonlocal SS equation in this section.

Theorem 4.1.Assume thatλjR≠ 0,λjI> 0,vj,0=(a1j,a2j,a3j,a4j,1)T,(1≤j≤2N1),whereλjR,λjIdenote real and imaginary parts ofλj,respectively.The nonlocal SS equation has the 2N1-soliton solution

whereM=(mkj)2N1×2N1satisfies

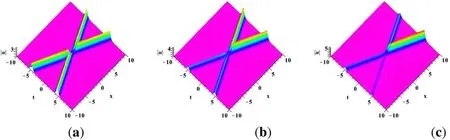
Figure 1.2N1-soliton with N1=1,λ1=0.2+0.8i by choosing suitable parameters:(a) a11=a21=a31=a41=0.4+i,;(b)a11=a21=0.4+i,a31=a41=0.4;(c) a21=0.4+i,a11=a31=a41=0.4.

Proof.Based on equations(46)-(47)and equations(65)-(66),one can easily obtain this solution.

Furthermore,we can write the 2N1-soliton solution as determinant form

where H is given by

with

Theorem4.2.AssumethatλjR=0,λjI> 0,vj,0=(b1j,b2j,b3j,b4j,1)T,(1≤j≤N2).The N2-soliton solution is

where

andM=(mkj)N2×N2with

Proof.Based on (56) and (65)-(66),the N2-soliton solution(72) is derived.

Taking N2=1 in the solution (72),one yields the single soliton solution as follows

Figure 2.2N1-soliton with N1=1,λ1=0.4+0.8i by choosing suitable parameters:(a) a11=a21=a31=a41=0.4+i;(b) a11=0.4+i,a21=a31=a41=0;(c) a21=0.4+i,a11=a31=a41=0.4.

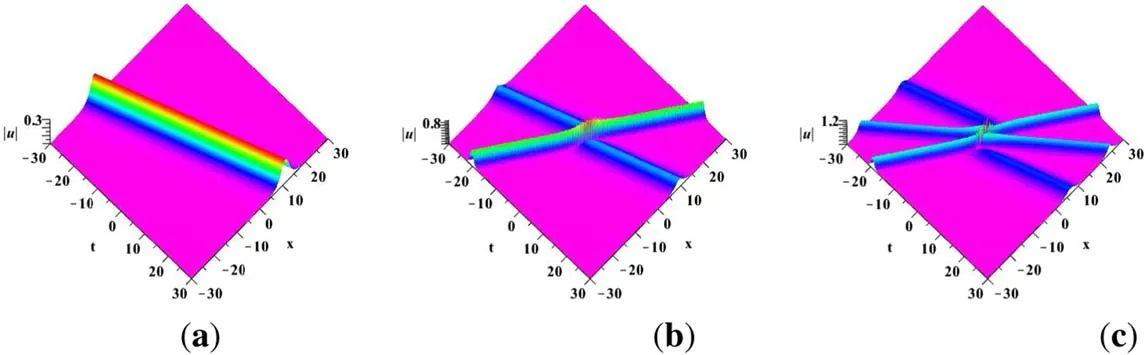
Figure 3.N2-soliton with N2=2 by choosing suitable parameters: b11=b21=b31=b41=b12=b22=b32=b42=b13=b23=b33=b43,(a) λ1=0.3i,b11=0.6;(b) λ1=0.3i,λ2=0.6i,b11=b12=0.6;(c) λ1=0.3i,λ2=0.6i,λ3=0.45i,b11=b12=b13=0.6.

Now,we graphically illustrate the 2N1-soliton solution(67) with N1=1 in figure 1.By choosing three classes of parameters figures 1-2 display the propagation process of two-soliton on (x,t) plane.We let λ1=0.2+0.8i in figure 1.There is a crossing state of two solitons.If a11=a21=a31=a41=0.4+i is held,then one shows two solitons with the same amplitude.As shown in figure 1(b),if a11=a21=0.4+i,a31=a41=0.4 is satisfied,the left and right sides of the solitons are asymmetric and the amplitude of the left side has declined significantly.We further let a21=0.4+i,a11=a31=a41=0.4,three quarters of soliton decreases.Actually,this is different from figure 2.If we suppose a21=a31=a41=0 or a11=a31=a41=0,figures 2(b),(c) exhibits two single solitons with asymmetric shape.the two-soliton in figure 2(a)can be regarded as an incomplete superposition state of these two single solitons.That is a type of inelastic collision behavior.Since the eigenvalues λi,i=1,2,… for the N2-soliton solution are purely imaginary,thus we let λ1=0.3i,λ1=0.6i,λ1=0.45i in the solution (72) with N2=1,2,3.As shown in figure 3,there are one-,two-and three-soliton,which are similar to the 2N1-soliton.The latter can be regarded as the even order soliton.One can present an even number of solitons when N1is chosen as any positive integer.As shown in figure 4,2N1+N2-soliton solution with N1=N2=1 presents a degenerate process of soliton by setting suitable parameters.Especially,4(a) shows a collision of the single soliton and two-soliton entanglement so-called bound state.However,if we take b11=0 and keep other parameter values,then there is a two-soliton keeping a crossing shape.Letting a11=a12=a13=0 in the solution only a single soliton is exhibited.This complete superposition process is similar to figure 2.Although three types of soliton solutions display the interaction behaviors of multi-soliton via suitable parameter values.For the first type of soliton solution,there exist inelastic collision behaviors when one changes some parameters.That is to say,they are incomplete superposition behaviors.Compared with the expressions of the 2N1-soliton solution and N2-soliton solution,we can find the latter is part of the former.The third type of soliton solution exhibits the combination of a single soliton and a two-soliton,in which a single soliton combines with one of the two-soliton to form a bound state.This result is different from the first two soliton solutions.If we increase the value of N2,2N1+N2-soliton solution can generate more bound solitons.

Theorem 4.3.The nonlocal SS equation has the 2N1+N2-soliton solution

whereM=(mkj)(2N1+N2)×(2N1+N2)with

Also,2N1+N2-soliton solution can be reduced to the determinant form

where Σ is given by

with

5.Conclusions

In this work,the Riemann-Hilbert problem and the three types of soliton solutions for the physically meaningful nonlocal integrable Sasa-Satsuma equation have been studied.We constructed a single soliton solution of the nonlocal Sasa-Satsuma equation from the reduction of those of the local Sasa-Satsuma equation.Based on that,the multi-soliton solutions of the nonlocal Sasa-Satsuma equation have been constructed and verified by using an algebraic method.In order to explain the dynamic characteristics of soliton solutions better,some soliton dynamics were theoretically and graphically explored.The method presented in this work is a pure algebra method,which can be effectively used to study other nonlocal nonlinear integrable models and the dynamics of soliton collision.

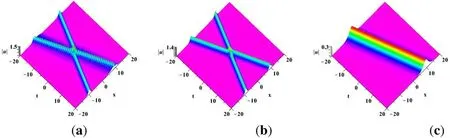
Figure 4.(2N1+N2)-soliton with N1=N2=1 by choosing suitable parameters:λ1=0.5+0.8i,λ3=0.3i,a11=a21=a31=a41,a12=a22=a32=a42,a13=a23=a33=a43,b11=b21=b31=b41 (a) a11=a12=a13=0.4,b11=0.6;(b) a11=a12=a13=0.4,b11=0;(c) a11=a12=a13=0,b11=0.6.

Acknowledgments

The authors would like to thank the Editor and Reviewers for their valuable comments.The work of Y Chen was supported by the Fundamental Research Funds for the Central Universities (Grant No.2022FRFK060015).The work of XW Yan was supported by the China Postdoctoral Science Foundation (Grant No.2022M710969) and the National Natural Science Foundation of China (No.12101159).

Data availability statements

The data used to support the findings of this study are available from the corresponding author upon request.

Compliance with ethical standards

Conflict of interest

The authors declare that they have no conflict of interest.

ORCID iDs