具有Neumann边界条件曲率方程解的估计
吴婷婷, 韩 菲, 孙文静
(新疆师范大学 数学科学学院, 新疆 乌鲁木齐 830017)
0 引言
十八世纪产生了偏微分方程这门学科,一开始偏微分方程问题主要来源于物理和几何问题,偏微分方程的研究在十九世纪得到了飞快地发展,这门学科现在已经成为当代数学中不可缺少的一部分,许多领域中的数学模型都可以用偏微分方程来描述.在偏微分方程课程的学习中,曲面的平均曲率是一个非常重要的概念,并且,平均曲率方程在几何偏微分方程中也是一个基础且重要的一类方程,因此,很多数学家研究其解的存在性并给出解的先验估计.
假设Ω是Rn中的光滑有界区域,u是Ω上的光滑函数.那么u的图的平均曲率可以表示为
设u是定义在[0,1]上的光滑函数,则对应的曲线的曲率为

(1)
平均曲率方程通常具有以下两种形式,当描述的u(·,t)的图是以平均曲率的大小和方向移动的曲面时,描述的方程可以表示为
当描述的u(·,t)的图是以平均曲率大小沿着xn+1的方向移动时,描述的方程可以表示为
对于上述两种形式的平均曲率方程已经被很多学者研究[1-5].
Guan[6]研究了当n≥2时,下面的预定夹角边界值条件的平均曲率方程

赵晓阳考虑的是下面的平均曲率流方程[7]
其中fz(x,z)≥-κ,κ>0,Ω∈Rn为有界的C3区域,n≥2,T为固定的正常数,并且得到估计
接下来,研究与式(1)相关的方程

(2)
其中f(x,u,Du)是定义在Ω×R×Rn上的光滑函数.
基于抛物偏微分方程解的梯度估计证明[9-10],构造合适的辅助函数,利用极大值原理推出一类抛物型方程中关于f依赖于x,u,Du时解的梯度估计的结果.
1 主要结果

(3)

(4)
u(x,0)=u0(x) ,x∈Ω
(5)

fz(x,z,p)≥-κ,κ≥0
(6)

(7)
|ψ(x)|C3(Ω)≤L2
(8)


(9)

引理1[8]假设对于固定的T>0,u∈C3(Ω)×[0,T]是方程(2)的解,并且有|u|≤M0,如果f(x,p,z)∈C1(Ω×[-M0,M0]×Rn)满足不等式(6)和不等式(7),则对任意的子区域Ω′⊂Ω,可以得到

下面将给出一些定义和符号,并且对ut进行估计.
记Ω为Rn中的有界区域,n≥2,∂Ω∈C3,并且记
d(x)=dist(x,∂Ω),Ωμ={x∈Ω:d(x)<μ},
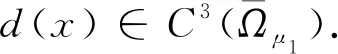
|Dν|+|D2ν|≤C(n,Ω)x∈Ωμ1
νiDjνi=0,νiDiνj=0,|ν|=1,x∈Ωμ1
(10)
定义
Cij=δij-νiνj,x∈Ωμ1,
对于向量ξ∈R2,记ξ′表示具有第i分量为Cijξj的向量.所以

(11)
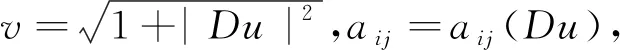
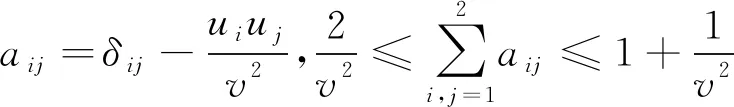
(12)
引理2 对于方程(3)-(5),假设fu≥-κ.则有估计式

先假设t0>0,则有两种可能性
(a)x0∈∂Ω.将方程(3)两边分别对t进行求导,得到

(13)
而

(14)
将式(13)代入式(14)可得
(fu(x,u)+k)e-κtut-fpl(x,u,Du)e-κtult.
由于fu≥-κ,则e-κtut满足椭圆方程的强极值原理.由边界条件可以得到utν=ψt=0,与Hopf引理矛盾.所以情况(a)不存在.

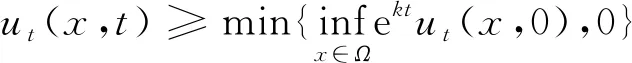
接下来证明定理1.根据Ma-Xu[4]中的方法,令w=u-ψ(x)d,选取下面的辅助函数
其中μ0是一个小于μ1的正常数,α,λ是正常数,并将在之后给出.

情形1x0∈∂Ωμ0∩Ω.通过引理2,可以得到梯度估计.
情形2x0∈∂Ω.证明方法与文[7]一致.
如果Φ(x)在(x0,t0)∈∂Ω×[0,T′]处达到最大值,那么在(x0,t0),有
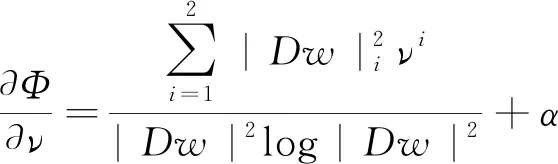
(15)
因为
wi=ui-ψxid-ψνi
(16)
在边界∂Ω上有

(17)
结合式(10),式(11)和式(17),可以得到

(18)
接下来,有
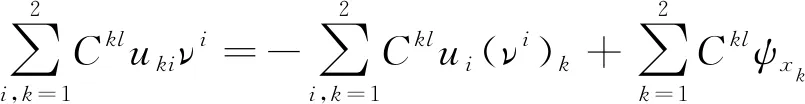
(19)
将式(19)代入到式(18)中,并结合式(4),式(15),有

(20)
根据式(16)可以在边界上得到
|Dw|2=|Du|2-ψ2.

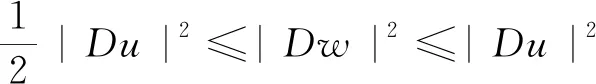
(21)
|Dw|2≥50
(22)
将式(21)和式(22)代入到式(20)中,可以得到
(α-|ψ|C0(Ω×[-M,M])-C0)|Dw|2log|Dw|2
=|Dw|2log|Dw|2>0,
其中取α=|ψ|C0(Ω×[-M,M])+C0+1,C0为只依赖于n,Ω的正常数,有
和Hopf引理矛盾,那么可以得到|Du|(x0)≤C.
情形3x0∈Ωμ0.在这个假设下,x0是Φ的临界点.在这里,使用w在x0处选择一个特殊的坐标系,使得
w1(x0,t0)=|Dw|(x0,t0)>0,w2(x0,t0)=0.
因为w=u-G,G=ψ(x)d,则wk=uk-Gxk,
因此,在(x0,t0)处,有
w1=u1-Gx1=u1-ψx1d-ψν1,
0=w2=u2-Gx2=u2-ψx2d-ψν2.
在(x0,t0)点,可以假设
u1≥200(|ψ|C0(Ω×[-M,M])+1) ,
否则,可以得到|Du|(x0)的界限,那么
通过前面的准备,可以将|Du|(x0,t0)的估计分成3个步骤.正如之前所描述的,所有的计算都是在固定点(x0,t0)来进行的.
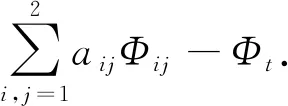
继续对Φt求导数
根据方程(3)
(23)
下面将得到|Dw|2的一阶和二阶导数

(24)
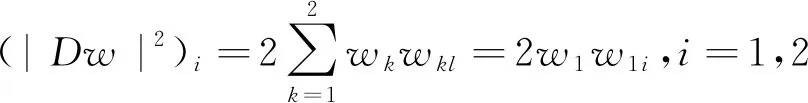
(25)
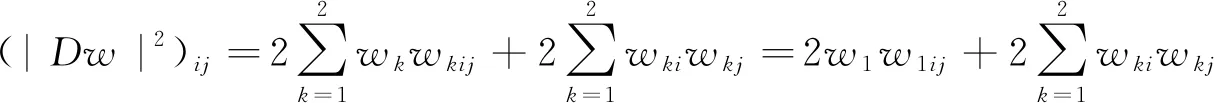
(26)
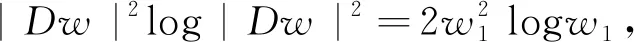
(27)
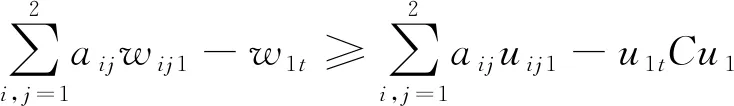
(28)
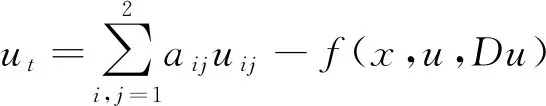

(29)
其中D1f=fx1+fuu1+fpmum1.根据式(12)可以得到

(30)
通过式(30)和式(29),可以得到

(31)
将式(31)代入到式(28),有
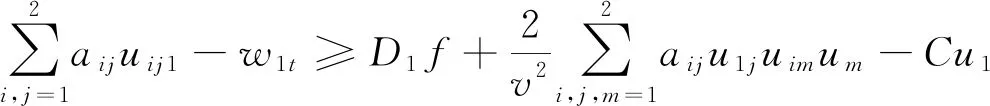
(32)
通过式(32)和式(27),得到
(33)
最后,将继续对式(33)的每一项进行估计.然后就结束证明并得到估计式(9).
根据Φi(x0,t0)=0和式(25),可以得到对i=1,2
w1i=-αw1logw1vi
(34)
将w1i=u1i-Gx1xi代入到式(34)中,根据选择的坐标系,可以得到对i=1,2
u1i=-αw1logw1vi+Gx1xi
(35)
通过式(34)和式(35),可以得到
(36)
并且根据不等式(6)和不等式(7),可以得到

(37)
将式(36),式(37)代入到式(33)中,最终得到
因此得到了在x0∈Ωμ0点的界限|Du|(x0,t0).
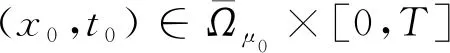
定理3的证明对于T>0,方程(7)在Ω×[0,T]上是一致抛物线方程.由定理1,引理2和ut估计,并结合偏微分方程的标准理论可以完成定理2的证明.
2 总结
研究结果主要是推广赵晓阳的抛物方程中关于f只依赖于x,u时该方程解的C0估计和C1估计,即抛物方程中关于f依赖于x,u,Du时该方程解的C0估计和C1估计.

