带马氏切换和时变时滞的随机神经网络的依分布渐近稳定性
王玉春, 王 莉
(1.宿迁学院 文理学院, 江苏 宿迁 223800; 2.中国矿业大学 数学学院, 江苏 徐州 221116)
0 引言
最近几十年,神经网络的研究受到了广泛关注,在各个领域中得到了广泛应用,如大脑中的神经回路,生态系统中的食物网和通信网络中的互联网等[1-3]. 在神经网络的电子实现中,信息在存储记忆和传递中一般会存在延迟现象,也称为时滞, 这种现象一般会引起系统的振荡,影响系统的稳定性. 另一方面,学者发现,在某些特殊情况下,在系统中引入时滞可以获得更好的系统性能[4],如带时滞的递归神经网络[5-7]得到了广泛的研究.
在进行神经网络的设计和应用时,研究系统的稳定性是必不可少的先决条件,目前稳定性的研究主要是在Lyapunov意义下的[8-9]. 另外,在实际应用中,系统的稳定性往往受一些不确定的随机因素的影响和干扰,包括外部不确定因素的扰动、传感器噪声和脉冲影响等会造成网络的不稳定。因此,随机神经网络系统的稳定性逐渐引起了学者们的关注,与确定性神经网络相比,其动力学行为会更复杂多变,这也给研究者带来了极大的挑战和兴趣,目前已经取得了很多较好的成果[7,10-11].
在随机神经网络中考虑马氏切换下的系统的稳定性,目前是一个新的研究方向[12-15].这类模型包含多个模式,不同的模式可以在一条马氏链的驱动下进行切换,在实际中有着潜在的应用价值. 如文[12]利用Lyapunov 稳定性理论,使用LMI分析技巧和矩阵理论,研究了具有随机扰动和马氏切换的中立型神经网络的自适应同步问题,给出系统同步的充分条件.文[14]研究了带马尔可夫跳的随机Hopfield神经网络的以分布渐近稳定性,给出了以分布渐近稳定性的充分条件. 但据作者所知,目前还没发现在随机神经网络中同时考虑马氏切换和时变时滞的文献.基于此,本文将马氏切换和时变时滞同时考虑到随机神经网络中,通过构造Lyapunov泛函,并利用伊藤公式和不等式放缩技巧,研究了系统的依分布渐近稳定的充分条件,并通过数值模拟验证所得结果的正确性.
1 模型描述
模型方程如下
(1)
模型中记号的含义说明如下
1)r(t),t≥0为一马氏过程,右连续,在S={1,2,…,N}内取值,Γ=(γij)N×N,(i,j∈S)为转换矩阵
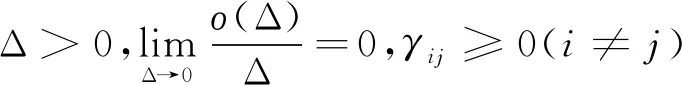
2) 向量x(t)=(x1(t),x2(t),…,xn(t))T∈Rn为神经元的状态,f(·)=(f1(·),f2(·),…fn(·))T为激活函数,A(r(t))=diag{a1(r(t)),a2(r(t)),…,an(r(t))},ai(r(t))>0(i=1,2,…,n)为行为函数,B(r(t))=(bij(r(t)))n×n,C(r(t))=(cij(r(t)))n×n代表反馈和时滞反馈阵,I(r(t))=(I1(r(t)),I2(r(t)),…,In(r(t)))T代表外部输入.σ=(σij)n×n是噪声强度阵,ω(t)=(ω1(t),ω2(t),…ωn(t))T∈Rn是定义在(Ω,F,{Ft}t≥0,P)上的n维布朗运动.记r(t)=i,A(r(t))=Ai,B(r(t))=Bi,(r(t))=Ci,I(r(t))=Ii,i∈S.
3) 0≤τ(t)≤h,τk(t)≤τ<1,其中h,τ都是大于零的常数.
另外,设矩阵H∈Rn×n,并且可表示为H=sI-B,s>0,B≥0,若s≥ρ(B),ρ(B)表示矩阵B的谱半径,则称矩阵H为M-矩阵[16].
为了对模型的稳定性进行分析,做如下假设.
假设1 激活函数f(·),对∀i∈S,t∈R+,x,y∈Rn,存在的正常数矩阵L满足
|f(x)-f(y)|≤L|x-y|,f(0)=0,σ(t,i,0)=0.
假设2对∀(t,i,x(t),x(t-τ(t)))∈R+×S×Rn×Rn,存在正对角阵T1,T2,满足
trace[σT(t,i,x(t),x(t-τ(t)))σ(t,i,x(t),x(t-τ(t)))]≤xT(t)T1x(t)+xT(t-τ(t))T2x(t-τ(t)).
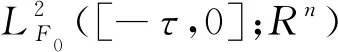
定义1[13]如果存在一个C([-τ,0];Rn)×S上的概率测度π(·,·)满足对∀(x,i)∈Rn×S,x(t)的转移概率p(t,i,x,dy×{j})当t→∞时弱收敛于π(dy×{j}),则称随机过程x(t)是依分布渐近稳定的.如果系统(1)的解x(t)是依分布渐近稳定的,则称系统(1)是依分布渐近稳定的.
引理1[14]如果存在函数V,U∈C1,2(R+×S×Rn,R+),μ,μ1∈H∞,μ2∈H和正数α,β,对∀i∈S,x,y∈Rn,有μ(|x|)≤V(t,i,x),LV(t,i,x)≤-αV(t,i,x)+β,U(t,i,0)=0,μ1(|x|)≤U(t,i,x),LU(t,i,x,y)≤-μ2(|x-y|)成立,则称系统(1)是依分布渐近稳定的.
引理2[15]设x,y∈Rn和ε>0,有xTy+yTx≤εxTx+ε-1yTy.
下面给出证明中会用到的Ito公式.令C1,2(R+×S×Rn;R+)代表在R+×S×Rn上对t一次可微,对x二次可微的非负函数V(t,i,x)的全体,对∀V(t,i,x)∈C1,2(R+×S×Rn;R+),广义的Ito公式定义如下
LV(t,i,x)=Vt(t,i,x)+Vx(t,i,x)[-A(r(t))x(t)+B(r(t))f(x(t))+
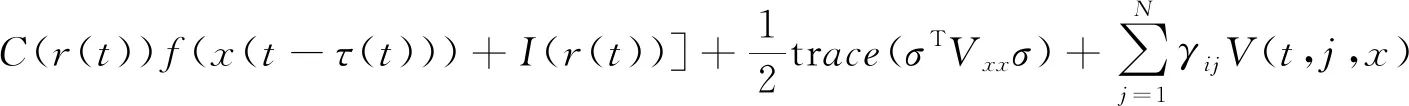
(2)
其中
2 主要结果
定理1如果假设1与假设2成立,那么若对∀i∈S,存在正定对称矩阵Di,常数ε1,ε2,ε3>0,使得
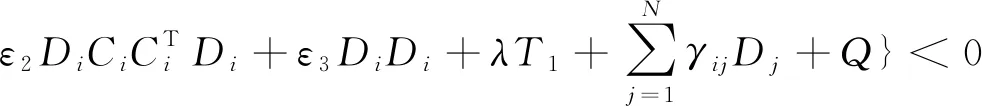
(3)
证明构造Lyapunov泛函

(4)
利用式(2)可得
LV(t,i,x)=2xT(t)Di[-Aix(t)+Bif(x(t))+Cif(x(t-τ(t)))+Ii]+
trace[σT(t,i,x(t),x(t-τ(t)))Diσ(t,i,x(t),x(t-τ(t)))]+
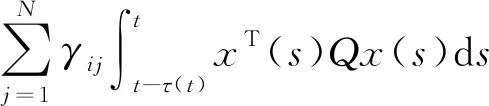
(5)
根据引理2及假设1和假设2,得
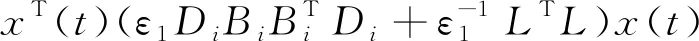
(6)
2xT(t)DiBif(x(t-τ(t)))≤
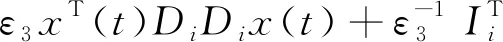
λ[xT(t)T1x(t)+xT(t-τ(t))T2x(t-τ(t))]-

(7)
把式(6)和式(7)代入式(5),得

(8)
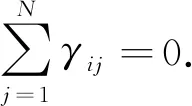
由式(8)知
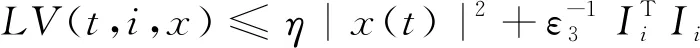
(9)
其中
由式(4)知

又由式(3)知,η<0,故由式(9),得
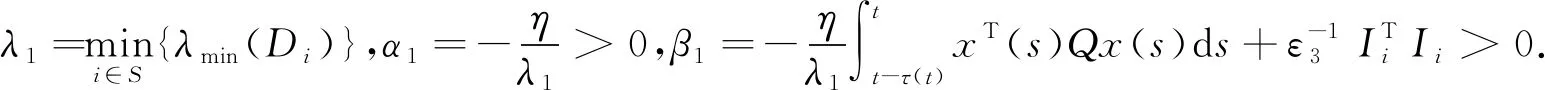
设x(t)、y(t)分别代表系统(1)初始值不相同时的两个解,则
d(x(t)-y(t))=[-Ai(x(t)-y(t))+Bi(f(x(t)-f(y(t)))+
Ci(f(x(t-τ(t)))-f(y(t-τ(t))))]dt+
[σ(t,i,x(t),x(t-τ(t)))-σ(t,i,y(t),y(t-τ(t)))]dω(t).
构造一个正定的Lyapunov泛函

类似可得LU(t,i,x,y)≤β2|x-y|2,其中
显然,β2<η<0,从而根据引理1,系统(1)是依分布渐近稳定的.
定理2如果假设1与假设2成立,若存在常数ε1,ε2,ε3>0,使得
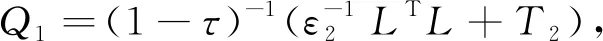
证明利用MK-矩阵的性质,存在q=(q1,q2,…,qN)T>0,满足(k1,k2,…,kN)T=Kq>0.取正定的Lyapunov泛函

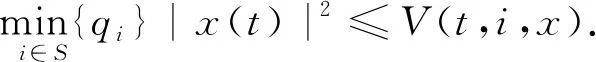
LV(t,i,x)=2qixT(t)[-Aix(t)+Bif(x(t))+Cif(x(t-τ(t)))+Ii]+
qitrace[σT(t,i,x(t),x(t-τ(t)))σ(t,i,x(t),x(t-τ(t)))]+
qixT(t)Q1x(t)-qixT(t-τ(t))(1-τ)Q1x(t-τ(t))+qixT(t)T1x(t)+
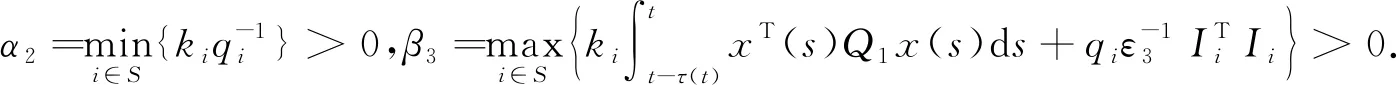
取下面正定的Lyapunov泛函

同理可得,可得

3 数值仿真
例1设r(t)是一个右连续的马氏过程,并且取值在S={1,2}内,其对应转换矩阵如下
考虑如下二维带Markov跳的随机变时滞随机神经网络模型
dx(t)=[-Aix(t)+Bif(x(t))+Cif(x(t-τ(t)))+Ii]dt+σ(t,i,x(t),x(t-τ(t)))dω(t)
(10)
其中

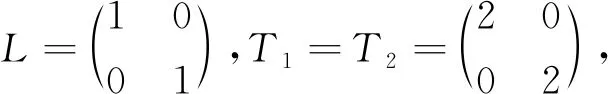
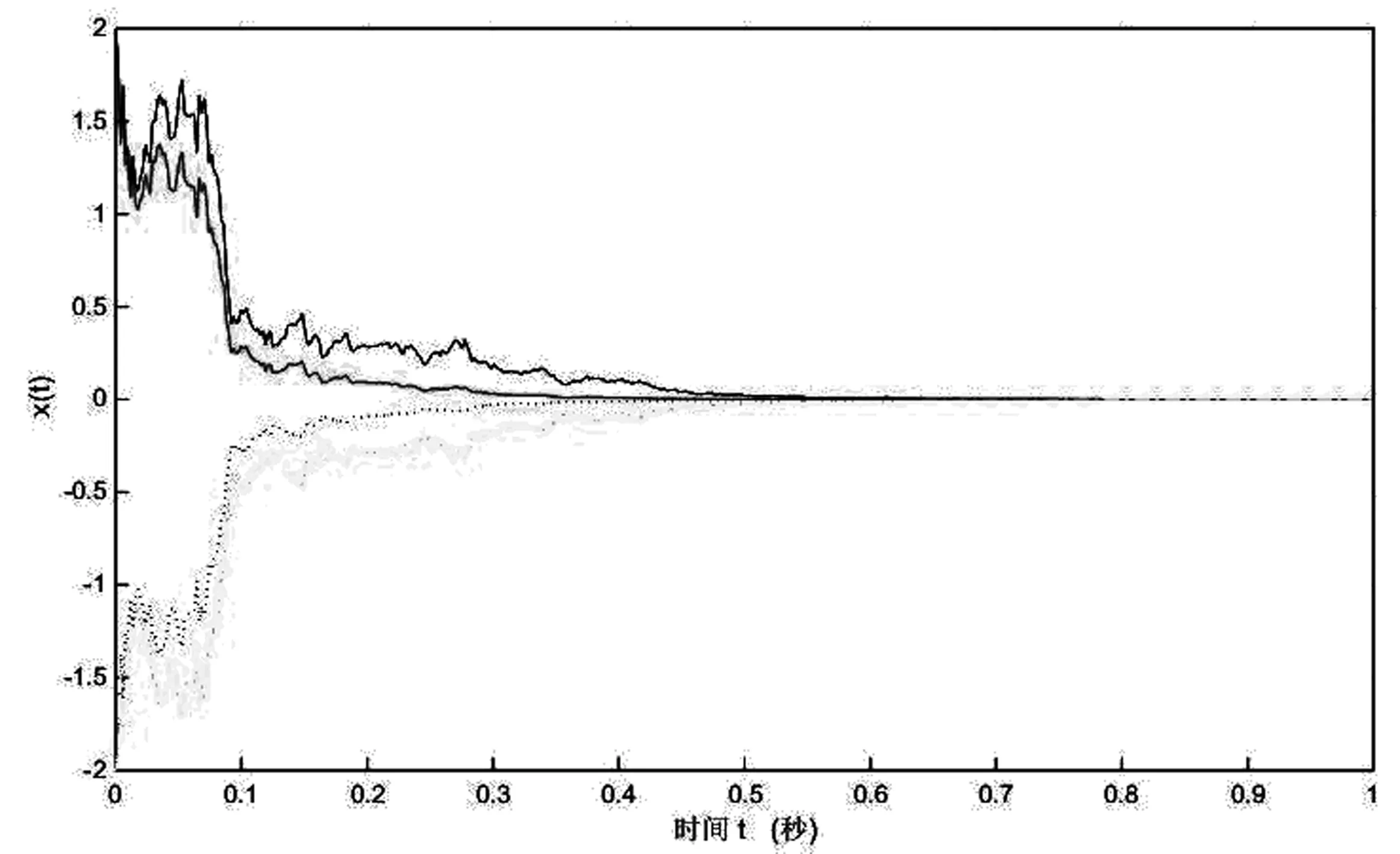
图1 系统(10)的动力学行为

