带间断系数的奇异摄动对流扩散方程的自适应移动网格方法

朱赐雯,刘利斌

(南宁师范大学广西应用数学中心,广西南宁 530100)

§1 引言

具有非光滑系数的奇异摄动微分方程广泛存在于流体力学,量子力学,弹性力学,化学反应器理论,气体多孔电极理论,气象学,海洋学等领域.这类问题的一个显著特点是高阶导数项包含一个摄动参数ε,且对流源项和右边源项在区域内部存在间断点.当ε →0时,这类问题的解在区域的边界和内部某个区域内会产生剧烈的振荡,即存在所谓的边界层和内层现象,参见[1].正因为边界层或内点层的出现,在很多情况下很难给出这类问题的精确解.迄今为止,针对具有连续系数的奇异摄动微分方程(即存在边界层),常用的数值方法主要有层适应网格方法(即Shishkin网格和Bakhvalov网格)和自适应移动网格算法[1].

在奇异摄动微分方程边界层问题的数值方法受到广泛关注的同时,一些具有间断系数的奇异摄动问题参数一致的数值方法也引起了广大学者的兴趣,并开展了一系列的研究.例如Farrell[2-3]等人分别在Shishkin网格和一类包含间断点的分段均匀网格上采用混合差分格式解决带间断系数的奇异摄动对流扩散方程,并证明了数值解几乎是一阶一致收敛的.针对带间断系数的双参数奇异摄动二阶常微分方程的边值问题,Prabha[4]等人在内层区域和其他区域使用了五点差分格式和标准中心差分格式的组合形式,得到了误差几乎是二阶收敛.岑仲迪[5]采用混合差分方法在Shishkin网格下研究一类带间断系数的奇异摄动对流扩散方程,并证明了该方法在最大范数上是二阶一致收敛的.此外,研究带间断系数的微分方程的数值方法还有Chandru[6]提出的包含不连续点的混合单调差分方法,和文献[7]中的迎风有限差分方法.考虑带间断系数的单参数奇异摄动抛物型问题或双参数的奇异摄动抛物型问题的过程中,学者们在均匀网格和特殊网格下分别构造了迎风有限差分格式和混合差分格式,并证明了数值格式的一致收敛性[8-11].

众所周知,网格的设计除了特殊网格和层适应网格外,还有自适应移动网格.自适应移动网格方法是一种基于后验误差估计的处理方法,该方法的关键是通过控制函数在问题的整个区间上构造自适应移动网格,使得边界层和内层区域分布的网格点较多[12-13].对于相同的奇异摄动问题,由算法构造的自适应移动网格比特殊网格更有效逼近精确解.如文献[13]中的作者对具有延迟项的奇异摄动微分方程设计了一个自适应移动网格算法,在他们的实验结果对比中明显看到自适应移动网格下的数值解和收敛阶比Shishkin网格要更精确.其他的奇异摄动问题如奇异摄动对流扩散方程或方程组问题,带参数的非线性奇异摄动问题等,同样可以在他们的实验结果对比中体现出自适应移动网格的优越性(参考文献[14-19]).但迄今为止,用自适应移动网格算法去处理带间断系数的奇异摄动微分方程的文献并没有出现.因此,本文仅在一维情况下研究了带间断系数的奇异摄动微分方程的自适应移动网格算法,方程为

其中0<ε ≪1是摄动参数,α1,α2是正的常数,Ωd=Ω-∪Ω+=(0,d)∪(d,1).对流项系数a(x)和函数f(x)在x=d ∈(0,1)处间断,在其他区域上是足够光滑的.在这些假设条件下,问题(1.1)有唯一解[2],且在x=d这一点处会出现振动现象,即有一个内层.

所以针对方程(1.1)的内层问题,在间断点与网格剖分的中点重合的网格下给出混合有限差分格式,基于解及其解的导数性质,解的正则和奇异分量的导数估计以及极大值原理,给出了相应的误差分析.再利用控制函数和网格等分布原理,对间断点前后部分网格分别构造了自适应网格生成算法.最后给出数值算例验证该算法的有效性.

注1.2在本文中,C是一个与ε和N无关的常数,且在不同的位置取不同的值.并且对于任意的函数u,ui表示u(xi).

§2 连续解的性质

本节研究问题(1.1)的解及其解的导数的一些性质,即极大值原理,连续解的稳定性及导数估计.

引理2.1(见[2]) 设u ∈C∩C2(Ωd)是问题(1.1)的精确解,满足u(0)≥0,u(1)≥0,且Lu(x)≥0,∀x ∈Ωd,[u](d)=0,[u′](d)≥0.则有u(x)≥0,∀(x)∈

引理2.2(见[2]) 设u(x)是问题(1.1)的解.其解满足下界

为了后面误差分析的方便,首先将问题(1.1)的解在区域[0,d]上分解为u=vL+wL,和在区域[d,1]上分解为u=vR+wR,且解的光滑层分量vL,vR满足

边界层部分wL,wR满足

引理2.3(见[5,p691]) 对整数0≤k ≤3,(2.1)-(2.5)的解vL,vR,wL,wR满足以下估计

§3 离散格式和自适应网格

首先将区间[0,d]和[d,1]分别分成N/2个小区间,即得如下非均匀网格

引理3.1(见[5,p694]) 假设uN是问题(3.1)的数值解,那么其解存在稳定性估计

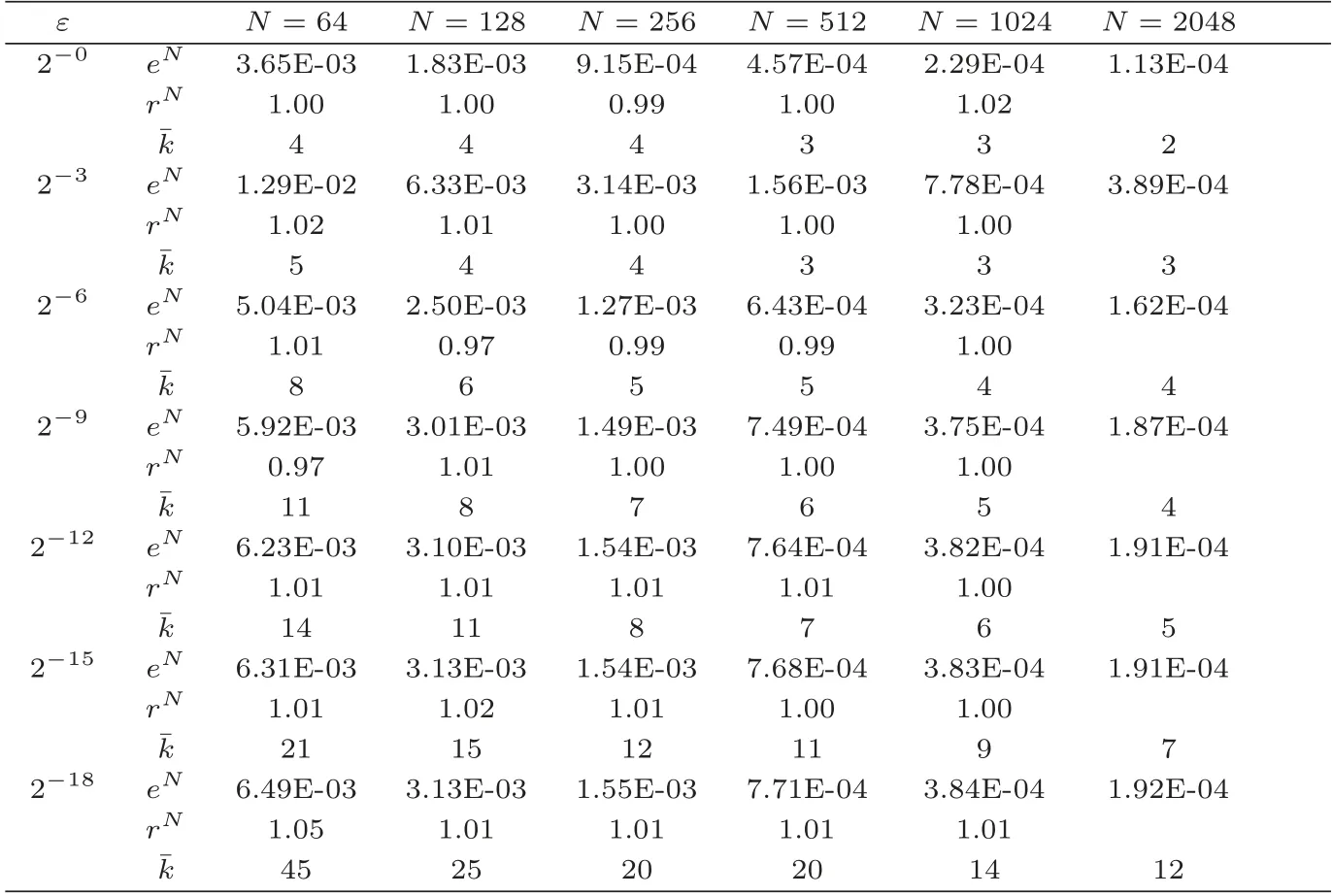
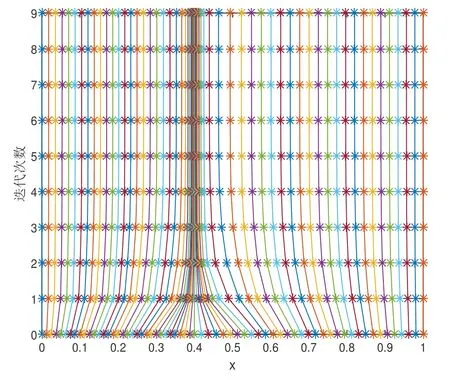
构造自适应网格算法的关键是对于给定的非负函数M(x),找到一组非均匀网格N={0=x0

则M(x)称为网格控制函数,(3.2)称为相应的网格等分布原理.

为了构造出问题(3.1)的自适应网格移动算法,选择控制函数

§4 误差估计

于是,为了推出离散格式的局部截断误差估计,先给出如下若干引理.

综上,引理4.2证明完成.

令TL,i,TR,i分别为离散格式(3.1)在区间[0,d)和[d,1] 上的局部截断误差,根据截断误差的定义,整合引理4.1和引理4.2得

当xi ∈[xk2,1],i ≥k2时,有hR,i ≥Cε,由引理3.3 以及(3.9)得ε ≤ChR,i ≤CN-1,根据截断误差定义,再利用中值定理可得

注4.1众所周知,若方程的条件数趋于无穷时,则导致矩阵奇异或者病态.因此,还要注意论文中方程的条件数是否趋于无穷.在文献[20]中作者推导出具有Dirichlet边界条件的方程为非齐次时,其方程的条件数为Cond eff=O(1/h),而当方程为齐次时，推导出的条件数为Cond eff=O(1),所以边界条件会影响着条件数.下面引用[20]中的引理进行说明.

引理4.6(见[20]中引理4.1) 设(3.1)的离散格式的系数矩阵为b,那么矩阵b存在上界为

引理4.7(见[20]中定理4.2) 在引理4.6的条件下,条件数Cond_eff满足

由上述的引理可以看出,当ε很小时,条件数Cond_eff→∞.但如果在实际计算过程中,通过变化把边界条件转变为0时,由引理4.7 得到条件数Cond_eff≤C‖f‖∞.则条件数与ε无关,从而不会影响解的稳定性.

§5 自适应网格生成算法

其中MN=MN-1.

§6 数值实验与结果分析

为了验证本文自适应网格算法的有效性,考虑如下奇异摄动对流扩散方程

由于该问题的精确解没有给出,采用下面公式来计算数值解的绝对误差

当ε=2-3k,k=0,1,···,6,N=2j,j=6,7,···,11时,表1 列出了自适应网格算法计算得到的最大误差和迭代次数,其中表1中每一个ε对应的第一行表示最大误差eN,第二行表示相应的收敛阶rN,第三行为上述网格生成算法的迭代次数.显然,由表1 的数据可以看出随着N的逐渐增大,本文提出的自适应网格算法能到达一阶收敛.为了进一步说明本文自适应移动网格算法的优势,将混合差分格式(3.1)分别在Shishkin网格和本文设计的自适应移动网格下计算出误差后进行比较,在表2 中可以看到两个网格的最大误差和收敛阶,通过对比明显看出在相同的ε和N的情况下,本文自适应移动网格算法的误差明显小于Shishkin网格的误差.

表1 自适应网格计算得到的数值结果

除此之外,当N=64,ε取不同值时,图1为上述自适应网格算法的数值解曲线图.当N=64,ε=2-8时,图2为上述自适应网格算法数值解的迭代过程.很明显由两个图可以看出,例子的解在x=d处出现了内层,自适应网格算法的网格点也明显向内层x=d处移动.

图1 数值解曲线图(N=64)

图2 网格迭代过程(ε=2-8,N=64)

§7 结论