Boussinesq方程稳态解的存在性与正则性
张敏心, 陈 敏, 罗 宏
(四川师范大学 数学科学学院, 四川 成都 610066)
Boussinesq方程由流体速度场与温度场耦合而成,是地球物理动力学中的重要模型,该方程被广泛应用于大气科学和海洋湍流研究[1-3],并且在Rayleigh-Benard对流研究中也发挥了重要作用[4].
本文主要研究如下的二维不可压缩Boussinesq方程
(1)
其中,Ω⊂R2是有界开集且有光滑边界∂Ω,u=(u1,u2)为速度场,T(x,t)为温度,p为压强,已知函数f和j分别表示外力和热源,正常数γ和κ分别表示黏性系数和热扩散系数,e2=(0,1).
Boussinesq方程的稳态解对于理解其动力学行为具有重要意义,关于二维Boussinesq系统的稳态解问题已经有了一些研究[5-12].1991年,Morimoto[5]利用Galerkin方法证明了在有界域中Boussinesq近似方程稳态解的存在唯一性.1996年,Lorca等[6]利用谱Galerkin方法结合不动点变元得到了广义Boussinesq方程解的存在性、正则性和唯一性条件.1998年,文献[7]证明了在外区域中的广义Boussinesq模型稳态弱解的存在性.2000年,Lee等[8]研究了二维稳态Boussinesq方程的最优控制问题,不仅证明了该方程光滑解和最优解的存在性,而且利用拉格朗日乘数法推导出一个最优系统.2011年,Alekseev等[9]考虑了在非齐次Dirichlet速度边界条件和混合温度边界条件下的黏性稳态Boussinesq方程最优控制的稳定性.2012年,Kim[10]利用经典的Banach不动点定理得到了在有界光滑区域上具有任意大边界条件的稳态Boussinesq系统极弱解的存在性,也证明了具有小边界条件的稳态Boussinesq系统极弱解的唯一性.2021年,黄娟丽等[11]采用分离变量法得到在水平与垂直条带区域上Boussinesq方程一些显式稳态解的结果.2022年,Chen等[12]用时间-权重能量估计,得到了在平面带区域上具有部分耗散的二维Boussinesq方程稳态解的整体存在性和稳定性,同时也建立了二维Boussinesq方程解的显式衰减率.
本文借助文献[13-14]的方法,研究二维Boussinesq方程稳态解的存在性与正则性.首先,利用弱连续算子锐角原理证明二维稳态Boussinesq方程弱解的存在性;其次,利用ADN理论以及线性椭圆方程理论证明方程强解的存在性,得到强解的范数估计式,并通过Sard-Smale定理得到解的有限性;最后,再次利用ADN理论以及线性椭圆方程理论得到方程古典解的存在性,实现了解的正则性的提升.
1 预备知识
本节介绍一些预备知识,包括弱连续算子锐角原理、ADN理论、线性椭圆方程理论和Sard-Smale定理等知识.
引理1.1[15]对于如下的椭圆方程:
(2)
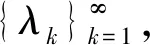
0<λ1≤λ2≤…,
λk→∞,k→∞.
引理 1.2[15-16](Sobolev嵌入定理) 令Ω⊂R2是一个有界开集,对任意区域Ω有:

Wk,p0(Ω)
特别地,这个嵌入是连续的,并且有以下不等式成立

其中,C=C(n,p)是依赖于n,p的常数.
设X是一个线性空间,X1、X2是Banach空间,X1是可分的,X2是自反的.设X⊂X2,于是存在一个线性映射L:X→X1是一一稠密的.
定义 1.1[15](弱连续算子的定义) 映射G:X2→X1*是弱连续的,如果对所有的{Φn}⊂X2,Φn⇀Φ0有
引理 1.3[15](弱连续算子锐角原理) 设G:X2→X1*是弱连续的,U⊂X2是有界开集,0∈U.若
〈G(Φ),LΦ〉≥0, ∀Φ∈∂U∩X,
则方程G(Φ)=0在X2中存在一个解.
引理 1.4[17-18](ADN理论) 考虑如下Stokes方程
(3)
则有如下结论:
1) 令(u,p)∈C2,α(Ω,Rn)×C1,α(Ω)是问题(3)的解.若f∈Ck,α(Ω,Rn),k≥0,则
(u,p)∈Ck+2,α(Ω,Rn)×Ck+1,α(Ω),
且满足如下估计
‖u‖Ck+2,α+‖p‖Ck+1,α≤
C(‖f‖Ck,α+‖(u,p)‖C0),
其中,C>0仅依赖于μ、n、k、α、Ω.
2) 令(u,p)∈W2,p(Ω,Rn)×W1,p(Ω)(1 (u,p)∈Wk+2,p(Ω,Rn)×Wk+1,p(Ω), 且有 ‖u‖Wk+2,p+‖p‖Wk+1,p≤ C(‖f‖Wk,p+‖(u,p)‖Lp), 这里C>0只依赖于μ、n、k、p、Ω. 引理 1.5[16](线性椭圆方程理论) 考虑如下椭圆方程 (4) 其中,aij,bi,c∈L∞(Ω),f∈L2(Ω),aij=aji是一致椭圆的,即存在常数0<λ1≤λ2使得 λ1|ξ|2≤aijξiξj≤λ2|ξ|2, ∀ξ∈Rn,x∈Ω, 则有如下结论成立: 1) 令Ω⊂R2是C2,α的,aij,bi,c,f∈C0,α(Ω).如果u∈C2,α(Ω,Rn)是问题(4)的解,那么 ‖u‖C2,α≤C(‖f‖C0,α+‖u‖C0), 其中,C>0仅依赖于n、α、λ、Ω和aij、bi、c的C0,α范数. 2) 令Ω⊂R2是C2的,aij∈C0(Ω),bi,c∈L∞(Ω),f∈Lp(Ω).如果u∈W2,p(Ω,Rn)是问题(4)的解,那么 ‖u‖W2,p≤C(‖f‖Lp+‖u‖Lp), 其中,C>0仅依赖于n、p、λ、Ω和aij、bi、c的C0范数或L∞范数. 引理 1.6[19-20](Sard-Smale定理) 令G:X→Y是C1的零指标的Fredholm算子,则G的正则值在Y中稠密.进一步,若p∈Y是G的临界点,则G-1(p)是一个离散集. 引入空间 H={Φ=(u,T)∈L2(Ω,R3)|Φ满足 H1=H1(Ω,R3)∩H. 证明对于∀Ψ=(v,s)∈H1,定义G:H1→H1*, fv-Tve2+κ▽T·▽s+(u·▽)T·s-js]dx. 首先,验证G算子满足 〈GΦ,Φ〉≥0. (5) 根据Young不等式以及Poincaré不等式,可得 κ▽T·▽T-jT)dx≥ ‖T‖‖u‖-‖j‖‖T‖≥ ‖j‖‖T‖= ‖f‖‖u‖-‖j‖‖T‖≥ 则存在恰当大的常数N使得 〈GΦ,Φ〉≥0, ∀Φ∈∂BN∩X, 于是(5)式成立. 再验证G的弱连续性.假设在空间H1中有Φk⇀Φ,根据引理1.2可得 uk→u0在Lp(Ω,R2)中,Tk→T0在 Lp(Ω)中,其中1≤p<∞. (6) dx+ dx= (7) 作下面分解 dx+ 由于在H01(Ω,R2)中有un⇀u0,即在L2(Ω,R2)中有Dun⇀Du0.同理,在H01(Ω)中有Tn⇀T0,即在L2(Ω)中有DTn⇀DT0,并且u0·v∈L2,u0·s∈L2,因此 dx=0, 由Hölder不等式和(6)式可得 dx|≤ 于是(7)式成立.由引理1.3可得,问题(1)存在一个弱解Φ∈H1. 证明由Hölder不等式,可得 (8) 考虑如下的Stokes方程 由f∈Lq(Ω,R2),T∈L2(Ω)和(8)式可知 因此,由引理1.4可得 对于椭圆方程: (10) 由j∈Lq(Ω)和(8)式可知 因此,由引理1.5可得 由引理1.2可得 1≤q≤6, 因此 于是可推出 (u·▽)u∈L2(Ω,R2), (u·▽)T∈L2(Ω). (11) 由(11)式、引理1.4和引理1.5可得 (u,T,p)∈W2,2(Ω,R2)×W2,2(Ω)×W1,2(Ω). 由引理1.2可得 1≤q<∞. 可以推出 (u·▽)u∈L3(Ω,R2), (u·▽)T∈L3(Ω). 利用引理1.4和引理1.5可得 (u,T,p)∈W2,3(Ω,R2)×W2,3(Ω)×W1,3(Ω). 如此重复以上步骤,便证得(1)式的解(u,T,p)∈W2,q(Ω,R2)×W2,q(Ω)×W1,q(Ω),q≥2. 证明对于(1)式的解(u,T,p)需要证明如下估计: ‖u‖W2,q+‖T‖W2,q+‖p‖W1,q≤ C(‖f‖Lq+‖j‖ q≥2. (12) 由引理1.4和(9)式可得 ‖u‖W2,q+‖p‖W1,q≤C‖g‖Lq≤ C(‖f‖Lq+‖T‖Lq+‖u·▽u‖Lq). 由引理1.5和(10)式可得 ‖T‖W2,q≤C‖h‖Lq≤ C(‖j‖Lq+‖u·▽T‖Lq), 因此 ‖u‖W2,q+‖T‖W2,q+‖p‖W1,q≤ C(‖f‖Lq+‖T‖Lq+‖u·▽u‖Lq+ ‖j‖Lq+‖u·▽T‖Lq). (13) 由Hölder不等式可得 ‖u·▽u‖Lq≤‖u‖L2q‖▽u‖L2q, ‖u·▽T‖Lq≤‖u‖L2q‖▽T‖L2q. (14) 由Gagliardo-Nirenberg不等式以及Young不等式可得 ‖▽u‖ ε‖Δu‖Lq+Cε-1‖▽u‖, (15) ‖▽T‖ ε‖ΔT‖Lq+Cε-1‖▽T‖. (16) 由〈GΦ,Φ〉=0,有 ‖▽u‖2+‖▽T‖2≤ C(‖f‖2+‖j‖2), 因此 ‖▽u‖≤C(‖f‖Lq+‖j‖Lq), ‖▽T‖≤C(‖f‖Lq+‖j‖Lq),q≥2.(17) 由引理1.2和(17)式有 ‖u‖L2q≤C‖▽u‖≤ C(‖f‖Lq+‖j‖Lq). (18) 由(14)、(15)、(17)和(18)式可以得到 ‖u·▽u‖Lq≤C(‖f‖Lq+‖j‖Lq)× [ε‖Δu‖Lq+Cε-1(‖f‖Lq+‖j‖Lq)]≤ C(ε‖f‖Lq‖Δu‖ 2ε-1‖f‖Lq‖j‖Lq+ 于是由Hölder不等式,可得 ‖u·▽u‖Lq≤C(ε‖f‖Lq‖Δu‖Lq+ ε‖j‖Lq‖Δu‖Lq). (19) 同理,由(14)式和(16)~(18)式可以得到 ‖u·▽T‖Lq≤C(‖f‖Lq+‖j‖Lq)× [ε‖ΔT‖Lq+Cε-1(‖f‖Lq+‖j‖Lq)]≤ C(ε‖f‖Lq‖ΔT‖ 2ε-1‖f‖Lq‖j‖Lq+ 于是由Hölder不等式,可得 ‖u·▽T‖Lq≤C(ε‖f‖Lq‖ΔT‖Lq+ ε‖j‖Lq‖ΔT‖Lq). (20) 由引理1.2和(17)式有 ‖T‖Lq≤C‖▽T‖≤ C(‖f‖Lq+‖j‖Lq). (21) 由(13)、(19)~(21)式有 ‖u‖W2,q+‖T‖W2,q+‖p‖W1,q≤ C[‖f‖Lq+‖j‖ ε(‖f‖Lq+‖j‖Lq)‖u‖W2,q+ ε(‖f‖Lq+‖j‖Lq)‖T‖W2,q]. (22) ‖u‖W2,q+‖T‖W2,q+‖p‖W1,q≤ C(‖f‖Lq+‖j‖ ‖j‖ (23) 最后利用Young不等式和(23)式证得(12)式成立. 最后,引入如下映射 G=L+H: W2,q(Ω,R3)×W1,q(Ω)→Lq(Ω,R3), 其中 令 于是方程(1)可以写成 1) 对任意(f,j)∈Cα(Ω,R3),问题(1)存在一个古典解(u,T,p)∈C2,α(Ω,R2)×C2,α(Ω)×C1,α(Ω); 3) 如果(f,j)∈C∞(Ω,R3),那么问题(1)的解(u,T,p)∈C∞(Ω,R4). 证明1) 因为Cα(Ω)⊂Lq(Ω),∀q≤∞,所以对任意(f,j)∈Cα(Ω,R3),由定理2.2可知问题(1)存在一个强解 (u,T,p)∈W2,q(Ω,R2)×W2,q(Ω)× W1,q(Ω), ∀q≥2. 由引理1.2知 W2,q(Ω,R2) 于是 (u,T)∈C1,α(Ω,R3), 因此 (u·▽)u∈Cα(Ω,R2), (u·▽)T∈Cα(Ω). 由(9)式中的g∈Cα和(10)式中的h∈Cα,以及引理1.4的结论1)可知 (u,p)∈C2,α(Ω,R2)×C1,α(Ω). 由引理1.5的结论1)可知 T∈C2,α(Ω), 即 (u,T,p)∈C2,α(Ω,R2)×C2,α(Ω)×C1,α(Ω). 结论1)成立. 2) 由于Cα(Ω)⊂Lq(Ω),∀q≤∞,再根据定理2.3可得,问题(1)的解是有限的. 3) 由于(f,j)∈C∞(Ω),有(f,j)∈Wk,q(Ω)(k是任意整数).根据定理2.2,可以得到(u,T,p)∈W2,q(Ω,R3)×W1,q(Ω).根据引理1.4以及引理1.5可得(u,T,p)∈Wk+2,q(Ω,R3)×Wk+1,q(Ω)(k是任意整数).利用引理1.2可得(u,T,p)∈Ck+1,α(Ω,R3)×Ck,α(Ω)(k是任意整数).于是(u,T,p)∈C∞(Ω,R4). 本文给出了Boussinesq方程稳态解存在的条件,得到强解的存在性和强解的范数估计,实现了解的正则性提升,并得到方程古典解的存在性. 本文考虑的Boussinesq方程形式相对简单,鉴于Boussinesq方程有很多的形式,比如具有水平(垂直)耗散、水平(垂直)热扩散、分数耗散的Boussinesq方程,对于是否能用弱连续算子方法考虑其他形式的Boussinesq方程解的存在性与正则性,将是进一步所需要考虑的问题.此外,本文讨论的是稳态Boussinesq方程解的存在性,对于是否能用弱连续算子方法研究演化Boussinesq方程解的存在性与正则性,也将是进一步所需要考虑的问题.2 主要结论






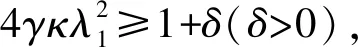

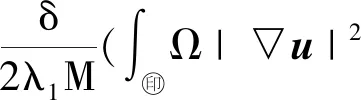


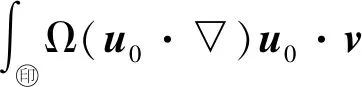
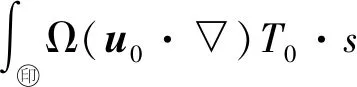
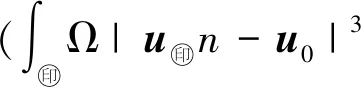
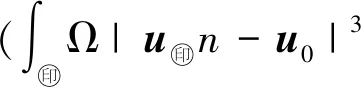




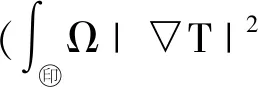
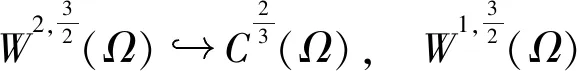

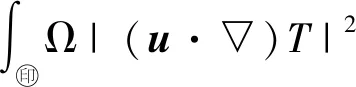



3 总结与展望

