基于混合策略改进的鹈鹕优化算法*
苏莹莹 任曼铜
(沈阳大学机械工程学院,辽宁 沈阳 110044)
鹈鹕优化算法(pelican optimization algorithm,POA)[1]是2022 年由Pavel Trojovský和Mohammad Dehghani 提出的一种新的自然启发优化算法。POA设计的主要思想是模拟鹈鹕在狩猎过程中的自然行为。该算法分为两个阶段,第一个阶段是向猎物移动(探索阶段),种群通过在搜索空间不断扫描获取猎物位置并向其移动;第二阶段是在水面上展翅(开采阶段),鹈鹕种群通过不断更新迭代获取最佳捕食位置。与经典的遗传算法、新兴的黑猩猩算法等群智能优化算法相比,POA 具有寻优能力强、参数较少、易于实现等优势。一些学者将POA 应用于工程领域,例如董青等[2]利用POA 建立桥架结构寿命预测的优化加点代理模型,实现对桥架结构安全性的预测;朱锡山等[3]提出一种新的鹈鹕优化算法-卷积神经网络-堆叠回归模型(POA-CNNREGST)对电梯钢丝绳滑移量进行预测,利用POA 对CNN-REGST 模型进行优化,提高了电梯安全状态评估的准确性。Al-Wesabi F 等[4]提出了一种在物联网中采用联邦学习驱动攻击检测和分类技术的鹈鹕优化算法(POAFL-DDC),利用POA 对DBN 超参数进行优化。结果表明,POAFL-DDC 取得了更好的结果。然而,POA 在捕食阶段,必须考察鹈鹕邻域范围才能收敛到较好解,因此基于邻域进行搜索时,虽然具有较强的局部搜索能力,但对全局的搜索能力不足。针对这些问题,Song H M等[5]提出了一种基于混沌干扰因子和初等数学函数的改进POA,在探索阶段引入了10 种不同的混沌干扰因子。选择出性能最优的改进POA 后,在POA 的利用阶段引入6 种不同的初等数学函数来提高其优化性能,但由于不同的混沌因子在处理不同测试函数时发挥的作用不同,因此整体优化结果有待加强。高猛等[6]利用Circle 映射对鹈鹕种群进行初始化,利用改进鹈鹕优化算法,建立极限梯度提升模型以提高电机故障诊断的准确度,虽然增加了初始种群的多样性,但仍无法解决鹈鹕算法后期易陷入局部最优的现象。周建新等[7]首先引入自适应权重提高算法寻优精度,然后结合正余弦算法提升算法性能,同时增加扰动因子防止种群陷入局部最优,并将改进鹈鹕优化算法与长短神经以及网络相结合,最后提升了钢坯温度的预测精度,但该算法的测试函数较少且精度有待进一步提升。
这些改进虽然在一定程度上提高了算法的性能,但在后期容易陷入局部最优,改进效果不够显著。为了进一步提高POA 的性能并检验该算法在实际应用中的效果,本文提出了一种基于混合策略改进鹈鹕优化算法。首先,在种群初始化阶段使用折射反向学习策略,扩大搜索空间,增加种群的多样性;其次,将正余弦优化算法运用到改进算法中,利用正余弦特性增强POA 算法全局与局部的搜索能力;然后,利用Levy 飞行策略,对鹈鹕个体进行变异,提高算法跳出局部最优的能力;最后,使用t分布变异提高后期收敛速度和精度。通过12 个不同的基准函数进行算法性能测试,比较IPOA 与已有的5 种经典算法海鸥优化算法(seagull optimization algorithm,SOA)、黑猩猩优化算法(chimp optimization algorithm,ChOA)、鲸鱼优化算法(whale optimization algorithm,WOA)、蛇群优化算法(snake optimizer,SO)和基本鹈鹕优化算法的仿真结果。结果表明,IPOA 算法具有更好的优化精度和更快的收敛速度。
1 改进鹈鹕搜索算法
1.1 鹈鹕优化算法
POA 由勘察阶段和开采阶段组成,流程如下:
首先鹈鹕种群根据问题的下界和上界利用方程随机初始化。
式中:xi,j为第i个候选解指定的第j个变量的值;N为种群成员个数;m为求解问题的维度;lj为问题变量的第j个下界,uj为第j个上界,rand为区间[0,1]内的随机数。
在提出的POA 中,每个种群成员是鹈鹕,是给定问题的一个候选解。完成初始化后,鹈鹕进入勘察阶段。在这一阶段,在解空间内随机生成猎物的位置,鹈鹕识别猎物的位置,然后向这个识别的区域移动,其表达式如下:
勘探阶段完成后,鹈鹕进入开采阶段。鹈鹕到达水面后,在水面上扇动翅膀将鱼体向上移动,在其咽喉囊中收集猎物。在这一阶段,算法考察鹈鹕位置邻域内的点,向狩猎区更好的点收敛,其表达式如下:
在第一阶段和第二阶段更新完所有种群成员后,基于种群的新状态和目标函数的值,更新到目前为止最好的候选解。算法进入下一次迭代,重复上述提出的POA 步骤,直到完全执行结束。最后,将算法迭代过程中得到的最佳候选解作为给定问题的准最优解。
1.2 改进鹈鹕搜索算法
1.2.1 折射反向学习机制策略
在种群初始化阶段,初始种群的质量对算法后期的求解过程及得出的结果均具有一定的影响。采用反向学习机制初始化种群个体的位置,可以使初始解在搜索空间中的分布更均匀。
反向学习(opposition-based learning,OBL)是由Tizhoosh H R[8]提出的一种扩大种群搜索范围的优化策略,其核心思想是其通过计算当前解的反向解,并选择较优解进行迭代,来找出给定问题的更优解,有利于提高算法的寻优效果。但在后期容易出现反向解落入局部最优区域的现象。结合光的折射原理而提出的折射反向学习(refracted oppositionbased learning,ROBL)[9]可以在不同程度上改善算法性能,扩大搜索空间。其原理如图1 所示。

图1 折射反向学习机制
在图1 中,以x轴为分界线,x轴上的解的搜索区间为[a,b],y轴表示法线,x轴上方有一光点从一种介质射入另一种介质,l为入射光线,l*为折射光线,α和β分别为入射角和折射角,a、b分布在点O两端。根据图中各参数的几何关系,可得折射率n的表达式为
令k=l/l∗,代入式(4)并将其拓展到多维空间可得折射方向解:
式中:xi,j代表该群体中第i只鹈鹕在j维上的位置;为xi,j的折射反向解;aj和bj分别表示搜索空间在j维上的下界和上界;k的大小决定了鹈鹕种群的位置,通过调整可以使种群向全局最优的位置靠近。
1.2.2 融合正弦余弦优化算法策略
正余弦算法(sine cosine algorithm,SCA)是2016 年由澳大利亚学者Mirjalili S[10]提出的基于数学性质的变化的新型元启发式优化算法。该算法通过迭代利用正弦余弦的变化对算法进行全局搜索和局部搜索,其个体的位置为
式中:t为当前迭代次数;Tmax为最大迭代次数。
正弦余弦优化算法[11]在迭代的过程中,通过不断更新参数r1,实现个体在参数r4的控制下选择正弦函数或余弦函数更新位置信息,从而更好地平衡算法的全局搜索能力与局部开发能力,当迭代到最大次数时,保存个体最优位置。
1.2.3 Levy 飞行机制策略
Levy 飞行[12]是一种非常有效地提供随机因子的数学方法,用来模拟自然界中的动物在不确定的环境中找寻食物的过程,并且服从莱维分布,是一种短距离探索与偶尔长距离行走相间的飞行方式[13]。
在标准的POA 开采阶段,在鹈鹕附近进行猎物的局部搜索时,随着迭代次数的增加,在最优解附近邻域内的鹈鹕容易陷入局部最优。为此,本文在鹈鹕在开采阶段引入Levy 飞行机制,对鹈鹕个体进行变异,扩大搜索半径,增加种群多样性,避免陷入局部最优,增强全局探索能力。在开采阶段,改进后的鹈鹕位置更新方式如下:
式中:Γ为标准Gamma 函数;β为[0,2]内随机数;r5为[0,1]内随机数;参数u、v为服从式(10)所示的正态分布随机数。
使用Levy 飞行机制的位置更新方程为
1.2.4 基于迭代次数的t分布变异
t分布又称为学生t分 布(student’st-distribution)[14],其含有的参数自由度n影响着函数曲线的形态,自由度n取值越小,曲线中部越平缓。n=1 时,t(n=1)→C(0,1);n=∞ 时,t(n=∞)→N(0,1)。其中,C(0,1) 为柯西分布,N(0,1)为高斯分布,即柯西分布和高斯分布是t分布自由度取1 和 ∞时的两个边界特例,其函数分布如图2 所示。
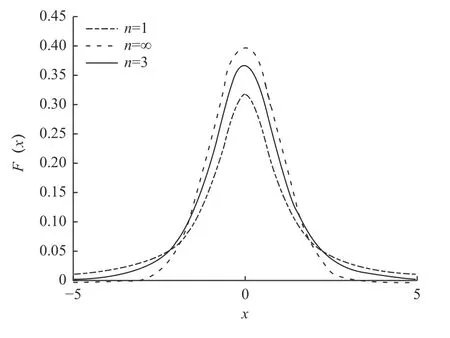
图2 t 分布函数分布图
为进一步提高算法的寻优性能,防止其在迭代后期陷入局部最优,本文对鹈鹕个体的位置进行自适应t分布变异,定义如下:
自适应t分布变异[15]以算法的迭代次数作为t分布的自由度参数。在算法运行前期,由于迭代次数较小,自由度n取值较小,曲线中部比较平缓,此时算法具有较好的全局探索能力;随着迭代次数的增加,自由度n逐渐增大,曲线中部凸起,此时算法具有较好的局部开发能力;当自由度无穷大时,t分布变异蜕变为标准正态分布。因此,t分布变异结合了柯西分布和高斯分布的特点和优势,同时具有全局探索能力和局部开发能力。
1.2.5 混合策略改进鹈鹕优化算法步骤
步骤一:设置算法参数和种群数量。
步骤二:反向折射学习机制初始化种群。
步骤三:计算适应度值,在搜索空间中随机生成猎物。
步骤四:根据式(6)更新鹈鹕位置。
步骤五:根据式(11)更新鹈鹕位置。
步骤六:对最优个体按照式(12)进行t分布变异。
步骤七:判断是否达到算法结束条件,若未达到,则跳转步骤三。
步骤八:记录最优结果,结束运行。
改进鹈鹕优化算法流程图如图3 所示。

图3 改进鹈鹕优化算法流程图
2 仿真实验和结果分析
2.1 不同算法比较
为了测试改进鹈鹕优化算法(IPOA)的整体性能,通过Matlab 对原始POA 和ChOA、WOA、SO、SOA 五种新兴的算法与IPOA 进行对比,利用12个基准函数进行测试。
本文实验均在相同环境下进行:64 位的Windows 11 系统,8G 内存,AMD Ryzen 7 6800H处理器,Matlab R2018b 仿真软件。基准测试函数见表1,其中F1~F6 为单峰函数,F7~F10 为多峰函数,F11 和F12 为固定维多峰函数。为了降低实验偶然性,仿真程序中设置种群大小为30,最大迭代次数为500。算法其他参数设置见表2。
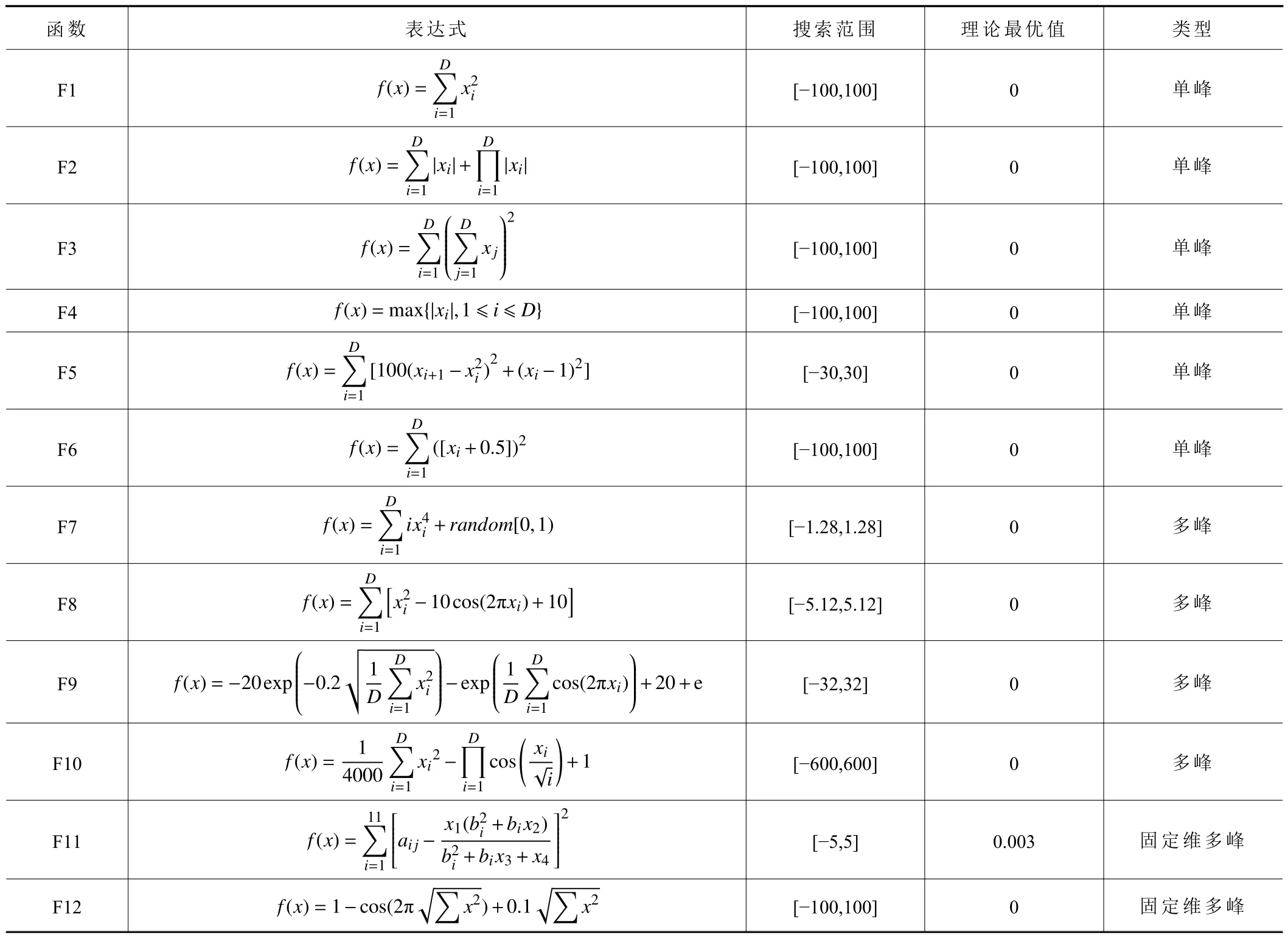
表1 12 个基准测试函数

表2 算法的参数设置
表3 给出了五种新型算法和IPOA 算法分别在12 个测试函数上运行30 次的结果,其中单峰函数的优化结果表明IPOA 具有较强的开发能力以逼近最优解,而多峰函数的优化结果表明IPOA 具有较强的在搜索空间中搜索最优区域的能力。从表3 可以看出,IPOA 算法在F1、F2、F3、F4、F8、F10、F12 的7 个测试函数上均能收敛到理论最优值,且标准差均为0,在求解质量、精度、稳定性、鲁棒性上都优于其他算法;对于F5、F6、F7、F9、F11这5 个函数,虽然没有收敛到理论最优值,但在稳定性上,IPOA 算法在很大程度上优于其他算法,说明其具有跳出局部最优的能力。相比于POA 算法,IPOA 在除F5 之外的11 个基准函数上的标准差与平均值均获得了显著的优势,进一步证明了改进算法策略的有效性。

表3 测试函数结果
为了更直观地反映出IPOA 算法的性能,本文给出算法在测试函数上的收敛曲线如图4 所示,可以看出,对于单峰函数,IPOA 算法在F1~F4 上的收敛速度和精度明显优于其他算法,在迭代次数不到300 时,IPOA 算法就已经找到理论最优值,这主要是因为IPOA 在种群初始化时利用反向折射学习扩大种群搜索范围,且在全局搜索阶段利用正余弦算法,更好地平衡了算法的全局搜索与局部开发能力,最后使用Levy 飞行机制摆脱局部最优的约束,加快算法的收敛速度与精度。对固定维多峰函数F12,其他算法均陷入了局部最优,而IPOA 的优化效果最好且最优值为0,说明改进策略提高了基本算法跳出局部最优的能力,证明了改进算法的可行性。

图4 测试函数收敛曲线图
2.2 不同改进策略性能分析
为对比不同改进策略的有效性以及对POA 性能提升的影响,将POA 与引入反向折射学习机制的鹈鹕优化算法(RPOA)、融合正余弦算法的鹈鹕优化算法(SCPOA)、融合Levy 飞行机制的鹈鹕优化算法(LPOA)、引入t分布变异的鹈鹕优化算法(TPOA)和POA 在12 种基准测试函数上进行对比,验证各自策略的有效性和混合策略改进POA 的优势。算法的实验参数与2.1 节一致,实验结果见表4。
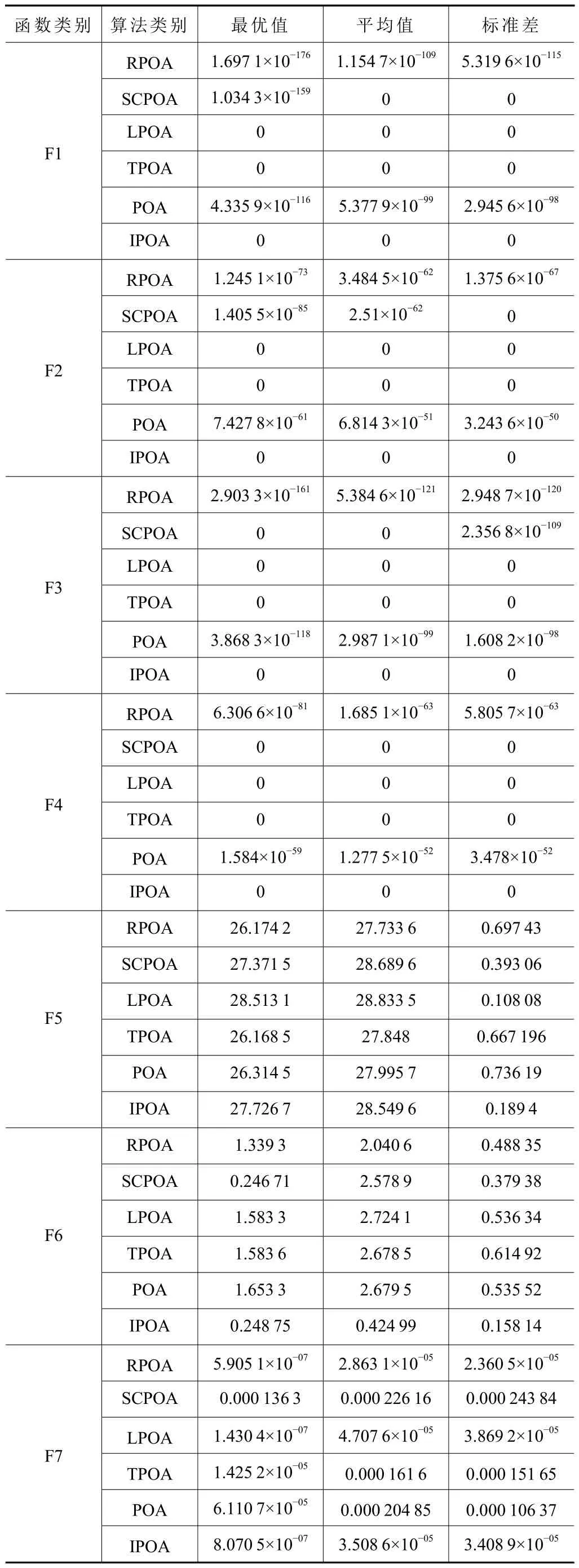
表4 不同改进策略算法的寻优结果对比
由表4 中数据可知,LPOA 和TPOA 在函数的寻优过程中起决定性作用,RPOA 和SCPOA 对函数的寻优也有一定的作用。对于单峰函数,在对F1~F4 寻优时,LPOA 和TPOA 均能找到理论最优值0;对于多峰函数,LPOA 和TPOA 在F7、F9、F11 未能找到理论最优值,但与POA 相比,寻优精度有一定的提升,从而证明了这两种策略的有效性。在函数F1~F7 的寻优上,RPOA 的寻优性能不是很明显,但相比于原始POA 还是有一定程度的提高,比如在对F1 寻优时,比POA 高了60 个数量级。SCPOA 在六个函数上的标准差都为0,且在F5、F11 寻优过程中各种改进策略均未找到最优值,但SCPOA 寻优贡献比其他策略大,说明其相较于POA 具有较强的稳定性和寻优精度。通过上述数据的比较,四种策略在对基础函数的求解上,每个改进策略对于算法寻优性能的提升均有一定效果,验证了各个策略的有效性。而综合了四种策略的IPOA 相较于结合一种策略的POA 具有更高的收敛性和精度,证明了混合策略的有效性。
3 IPOA 算法求解压力容器问题
为进一步验证算法性能,评估IPOA 在实际应用中的有效性,本文将IPOA 算法应用于压力容器结构设计中。压力容器是一种用于石油化工、能源工业、科研和军事工业等领域,承载一定压力的设备。压力容器是一个最小化问题,其设计目标是使其在耐压前提下,设计制作的总成本最小,其结构设计如图5 所示,容器的两端有盖子封顶,L为圆柱体部分的横截面长度,R为内部半径,Ts为圆柱体部分壁厚,Th为头部半圆的壁厚,L、R、Ts和Th为四个设计变量,问题的数学模型表示如下。

图5 压力容器问题示意图
分别用基本POA 算法和IPOA 算法对该问题进行求解,得到的结果见表5,可以看出,IPOA 在稳定性和寻找最优解上都具有显著优势。从压力容器收敛图6 可以直观地看出,IPOA 在100 代时已经开始收敛于最优值,但POA 接近250 代时才找到最优值,在收敛速度上IPOA 明显强于POA,所以IPOA 更能够有效地求解工程应用问题。

表5 压力容器设计问题求解结果

图6 压力容器设计求解收敛曲线图
4 结语
本文针对基本POA 算法的不足,通过引入折射反向学习机制、融合正余弦算法、Levy 飞行机制和基于迭代次数的t分布变异,提出了一种改进的IPOA 算法。首先利用反向折射学习得到初始种群,利用正余弦函数的震荡特性扩大搜索范围;然后在开采阶段引入Levy 飞行机制更新种群位置,避免算法陷入局部最优;最后利用以迭代次数作为自变量的t分布变异加快算法的收敛速度,提高算法寻优精度。将IPOA 与其他五种算法通过12 个经典测试函数进行检验比较,并通过压力容器优化设计问题进一步验证。结果表明,改进鹈鹕优化算法在全局寻优以及局部开发方面具有更优表现,验证了改进策略的有效性。

