Spin gap in quasi-one-dimensional S=3/2 antiferromagnet CoTi2O5
Hao-Hang Xu(徐浩航), Qing-Yuan Liu(刘庆元),5, Chao Xin(辛潮), Qin-Xin Shen(申沁鑫), Jun Luo(罗军),Rui Zhou(周睿), Jin-Guang Cheng(程金光), Jian Liu(刘健), Ling-Ling Tao(陶玲玲), Zhi-Guo Liu(刘志国),Ming-Xue Huo(霍明学), Xian-Jie Wang(王先杰), and Yu Sui(隋郁),,†
1School of Physics,Harbin Institute of Technology,Harbin 150001,China
2School of Science,Changchun University of Science and Technology,Changchun 130022,China
3Beijing National Laboratory for Condensed Matter Physics,and Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China
4Laboratory for Space Environment and Physical Sciences,Harbin Institute of Technology,Harbin 150001,China
5Southwest Institute of Applied Magnetics,Mianyang 621000,China
Keywords: quasi-one-dimensional antiferromagnet,magnetic anisotropy,spin gap
1.Introduction
Low-dimensional quantum magnets have been attracting much attention due to their fascinating phenomena, such as Bose-Einstein condensation, quantum spin liquids, and multiferroics.[1-3]Among various low-dimensional materials, the 1D magnets with a spin gap are of particular interest because they can host many exotic ground states, such as the field-induced gapless quantum spin liquid state in BaCo2V2O8,[4]and the pressure-induced superconductivity in Sr2Ca12Cu24O41.[5]In general, for a uniform 1D Heisenberg antiferromagnetic spin chain,the value of the spin quantum numberSdetermines the appearance of the spin gap in the excited states.[6]The spin gap can only be observed in 1D Heisenberg antiferromagnets with integer spins, e.g.,PbNi2V2O8withS= 1, in which a Haldane gap exists in the magnetic excitation spectrum,[7]while a gapless magnetic ground state can be seen whenSis half-integer.However,in some special cases, 1D antiferromagnets with half-integer spins also exhibit the gapped ground state by breaking the translation symmetry of spin.[8-10]For example, in the spin-Peierls compound CuGeO3, the dimerization of Cu2+withS= 1/2 not only leads to the structural transition but also opens a spin gap in the magnetic excitation spectrum.[11]In addition, the spin gap was also found in some 1DS=1/2 antiferromagnets with special crystal and magnetic structures,such as Cu benzoate and BaCo2V2O8.[12-14]For Cu benzoate with alternating crystal axes,it shows a field-induced spin gap because a non-collinear spin arrangement can be induced by applying a magnetic field perpendicular to the spin chain,and the canted spins are stabilized by the internal effective field along the chain.[15]However, in the case of BaCo2V2O8, the non-collinear magnetic structure is generated by the screw chain of Co2+and stabilized by the interchain exchange interaction.Thus, the spin gap in BaCo2V2O8opens with the 3D long-range magnetic ordering under zero field and can be closed under the magnetic field of about 40 kOe,followed by the field-induced order-to-disorder phase transition.[13,16]
The spin chain of Co2+could also exist in the pseudobrookite CoTi2O5, which belongs to the orthorhombic crystal system with aCmcmspace group.The CoTi2O5consists of two inequivalent TM1O6and TM2O6octahedrons with a ratio of 1:2, where TM represents Co2+/Ti4+cations.In comparison to the TM2O6octahedron, the TM1O6octahedron in pseudobrookite compounds is larger and more distorted.Therefore, the cation order-disorder always occurs in pseudobrookite compounds.For the completely ordered CoTi2O5, as shown in Fig.1(a), the larger TM1O6octahedron can only be occupied by the Co2+(r=0.74 °A),and the nonmagnetic Ti4+(r=0.68 °A)occupies the TM2O6octahedron, just like the well-studied pseudobrookite MgTi2O5.[17]In this situation, the distances between different Co2+along thebandcdirections are much greater than that along thea-axis (a= 3.72649 °A,b= 9.7005 °A,c= 10.0731 °A),[18]so a 1D chain of Co2+could form along thea-axis, making CoTi2O5an example of a quasi-1D antiferromagnet with spinS=3/2.
Recently, Kirschneret al.reported that CoTi2O5shows an unexpected long-range antiferromagnetic ordering atTN=26 K, though there is a strong frustration of Co2+according to the magnetic structure of CoTi2O5.[18]They proposed that there could be the spin Jahn-Teller effect in CoTi2O5, which lowers the structural symmetry and relieves the frustration,and in turn,leads to the appearance of the magnetic transition.However,the nature of CoTi2O5as a 1D antiferromagnet has yet to be reported and whether a spin gap exists in CoTi2O5is still unknown.In this work,we grew the CoTi2O5single crystals with highly ordered Co2+/Ti4+occupation by using the floating zone method and revealed that CoTi2O5is a quasi-1D Heisenberg antiferromagnet.The appearance of the spin-orbit coupling in CoTi2O5causes the obvious magnetic anisotropy,which opens a spin gap at low temperature.
2.Experiments
2.1.Single-crystal growth and characterization
CoTi2O5single crystals were prepared by the optical floating zone technique in an image furnace with two ellipsoidal mirrors (IR Image Furnace G3, Quantum Design Japan).[18,19]The crystals were grown in different atmospheres(pure Ar, pure O2, and Ar/O2mixed gas atmosphere) with a growth rate varying from 1 to 10 mm/h.CoTi2O5single crystal with highly ordered Co2+/Ti4+occupation was grown under pure Ar atmosphere with the growth rate of 1 mm/h.This gives a new approach for manipulating the ordering of cations and producing 1D spin chains.MgTi2O5single crystals were also prepared under the pure argon atmosphere with 1 mm/h to estimate the lattice specific heat of CoTi2O5.The phase purity was identified by the x-ray diffraction (XRD, Aeris, CuKα1radiation) and the x-ray Laue back diffraction was used to determine the crystal principal axes.Raman spectra were obtained with the LabRAM HR Evolution Raman Spectrometer(HORIBA).X-ray photoelectron spectroscopy(XPS)was measured with Esca Xi+(ThermoFisher).
2.2.Magnetization and thermal properties measurements
The temperature and magnetic-field dependencies of magnetizationM(T) andM(H) were recorded using a commercial SQUID magnetometer (MPMS3) up to the field of 70 kOe.The measurement of specific heatC(T) was performed with a physical property measurement system(PPMS,DynaCool-14 T).Both the thermal expansion ΔL/L0(T) and the magnetostriction ΔL/L0(H) were performed in the PPMS by using an AH 2550A capacitance dilatometer that was calibrated with 99.999%pure Cu and Al rods.The thermal conductivityκ(T)was measured in the PPMS with the method of one heater and two thermometers.
2.3.NMR measurements
In experiment,59Co NMR measurements were performed on a single crystal of CoTi2O5under a fixed magnetic fieldH= 90.743 kOe.The NMR spectra were obtained by integrating the spin echo as a function of frequency.The spin-lattice relaxation rate 1/T1was measured by the saturation-recovery method.The59CoT1was obtained by fitting the nuclear magnetizationM(t) with the equation 1-M(t)/M(0)=0.01191exp(-t/T1)+0.06818exp(-6t/T1)+0.20604exp(-15t/T1)+0.71387exp(-28t/T1), whereM(0)andM(t) are the nuclear magnetizations at the thermal equilibrium and at timet,respectively,after the comb pulse.
2.4.Theoretical calculations
All of our first-principles calculations were based on spinpolarized density functional theory (DFT) as implemented in the Viennaab initiosimulation package (VASP).[20,21]The Perdew-Burke-Ernzerhof functional revised for solids(PBEsol) was adopted for exchange-correlation potential.Generalized gradient approximation(GGA)[22]with the Hubbard parameter (GGA+U)[23]was employed to solve the Kohn-Sham equation.[24]The plane wave energy cutoff,convergence in energy, and residual force on each atom were set to 500 eV,1×10-5eV,and 0.01 eV/°A,respectively.To obtain the accurate magnetic structure, we built a 2×1×1 supercell, and the corresponding Brillouin zone integrations were set using a tetrahedron method in 8×8×8 Monkhorst-PackK-point mesh.[25]Magnetic anisotropy and spin-orbital coupling(SOC)were considered.The structure and spin density visualization and analysis were carried out using the VESTA code.[26]
3.Results and discussions
3.1.Controlling the degree of the ordering of Co2+/Ti4+in CoTi2O5
It was reported that the highly ordered cation occupation in the pseudobrookite ceramics can be obtained by using the high-pressure technique or by annealing the sample at a lower temperature.[17,27]In our previous work, we found that the single crystal of inverse spinel Mn2TiO4with ordered Mn2+/Ti4+occupation atBsites can be grown by the optical floating zone method under pure Ar atmosphere.[28]Thus,we prepared the CoTi2O5single crystals with different degrees of Co2+/Ti4+ordering by using the floating zone technique under pure Ar, pure O2, and the Ar/O2mixed gas atmosphere.The clear Laue diffraction spots show the high quality of our single crystal, as illustrated in Fig.1(c).The XPS spectra of Co-2p and Ti-2p show that the oxidation states of Co and Ti in the grown CoTi2O5sample are +2 and +4, respectively(details can be seen in Fig.S1 in the supplemental material).TheM(T) curves of crystals grown with different conditions were recorded to roughly check the degree of the ordering of Co2+/Ti4+because the character of the 1D magnets, usually represented by the broad peak at high temperature in theM(T)curves,depends on the degree of the ordering of Co2+/Ti4+in CoTi2O5.As shown in Fig.1(b),the broad peak inM(T)becomes more pronounced with decreasing oxygen content in the growth atmosphere,suggesting that Co2+/Ti4+tends to be ordered in the pure Ar atmosphere.Furthermore, when the growth rate is lowered,the magnetization below the magnetic ordering temperature decreases more rapidly, and the Curie tail gradually becomes weaker, revealing that the Co2+/Ti4+occupation becomes more ordered.
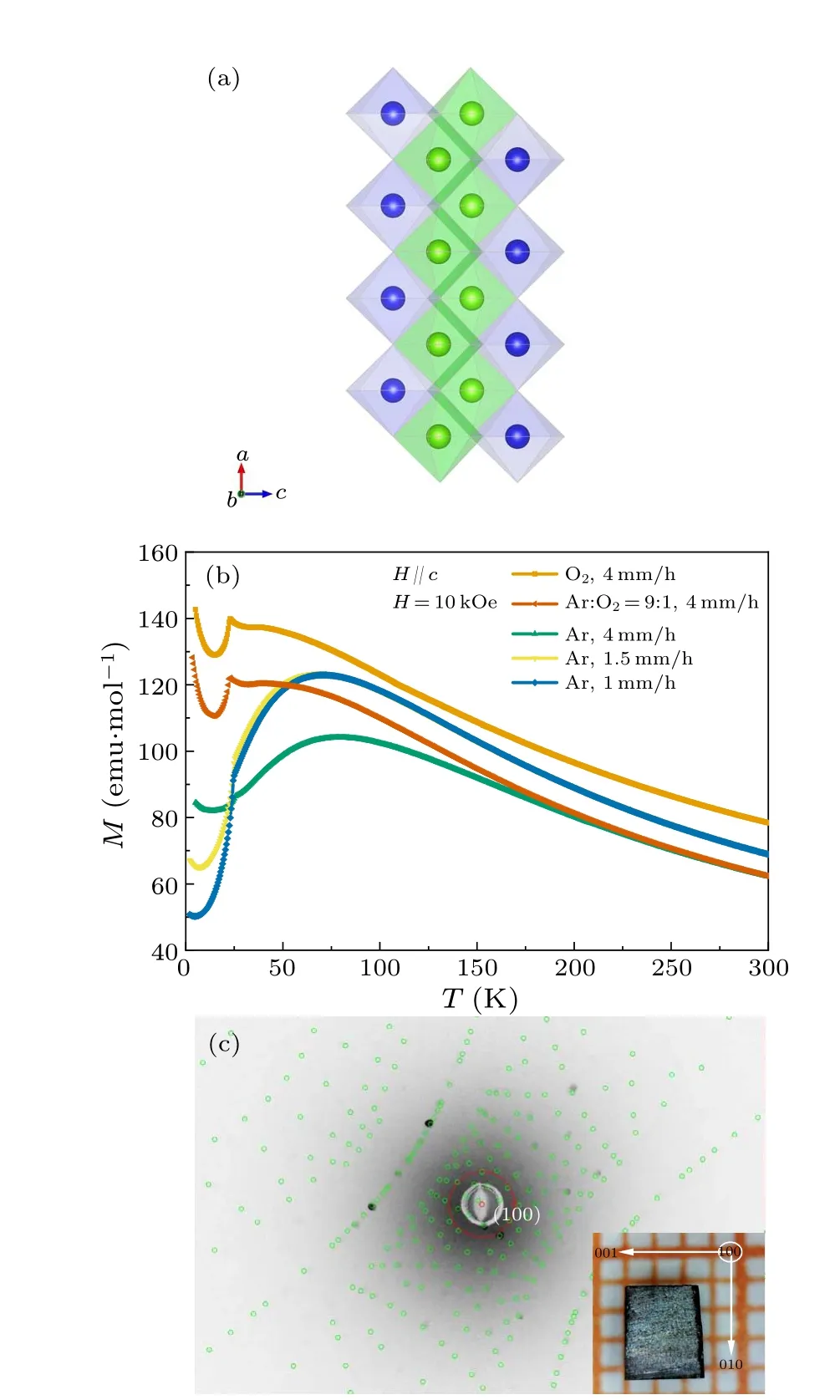
Fig.1.(a)Crystal structure of CoTi2O5.Co2+ and Ti4+ are labeled as blue and green balls,respectively.(b)The M(T)curves of CoTi2O5 single crystals prepared under different conditions.(c)Laue pattern taken from the CoTi2O5 single crystal along the[100]direction.Inset in(c)shows the oriented single crystal with three axes[100],[010],and[001].
3.2.Determining the degree of the ordering of Co2+/Ti4+in CoTi2O5
Raman spectra of CoTi2O5grown under different conditions were measured to estimate the degree of the ordering of Co2+/Ti4+.As shown by the asterisks in Fig.2(a), extra vibrate modes appear in the crystals prepared under the pure Ar atmosphere,consistent with the results of the well-studied MgTi2O5with highly ordered Mg2+/Ti4+occupation.[29]It was reported in MgTi2O5that the frequencyωof the B1g(5)Raman mode at 640(2) cm-1shows the blue shift with the Mg2+/Ti4+disorder increasing and can be used to determine the Mg2+/Ti4+disorder parameterXwith the relation[29]
whereXis defined as the atomic concentration of Ti4+in TM1 sites.The Raman spectra of CoTi2O5also show a similar blue shift,so the Co2+/Ti4+disorder parameterXfor the most ordered CoTi2O5is estimated to be in the range of[0.12, 0.18]by using formula (1), which is comparable with [0.15, 0.22]of highly ordered MgTi2O5prepared by annealing.[29,30](the blue shift in Raman spectra of CoTi2O5can be seen in Fig.S2 in the supplemental material).

Fig.2.(a)The Raman spectra of CoTi2O5 single crystals prepared under different conditions.(b)The Rietveld refinement results of CoTi2O5 prepared under pure Ar atmosphere with 1 mm/h.
From the powder XRD data of the most ordered CoTi2O5crystal, as shown in Fig.2(b), the lattice parameters of CoTi2O5are refined asa=3.72284(2) °A,b=9.70068(5) °A,andc=10.06784(5) °A,consistent with the results from neutron powder diffraction reported before.[18]The refinement results further give the Co2+/Ti4+disorder parameterXabout 0.13, showing that most of the Co2+occupy the TM1 sites,forming the Co2+chain along thea-axis.Thus, the CoTi2O5single crystal with highly ordered Co2+/Ti4+occupation can be grown in the pure Ar atmosphere at a growth rate of 1 mm/h.This provides a new way for controlling the ordering of cations and then generating 1D spin chains.The magnetization, the thermal physical properties, and the59Co nuclear magnetic resonance spectra measurements are all performed on the oriented CoTi2O5single crystals with the highest degree of the ordering of Co2+/Ti4+, which was grown in the pure Ar atmosphere at a growth rate of 1 mm/h(refined crystal structure parameters of CoTi2O5can be seen in Table S1 in the supplemental material).
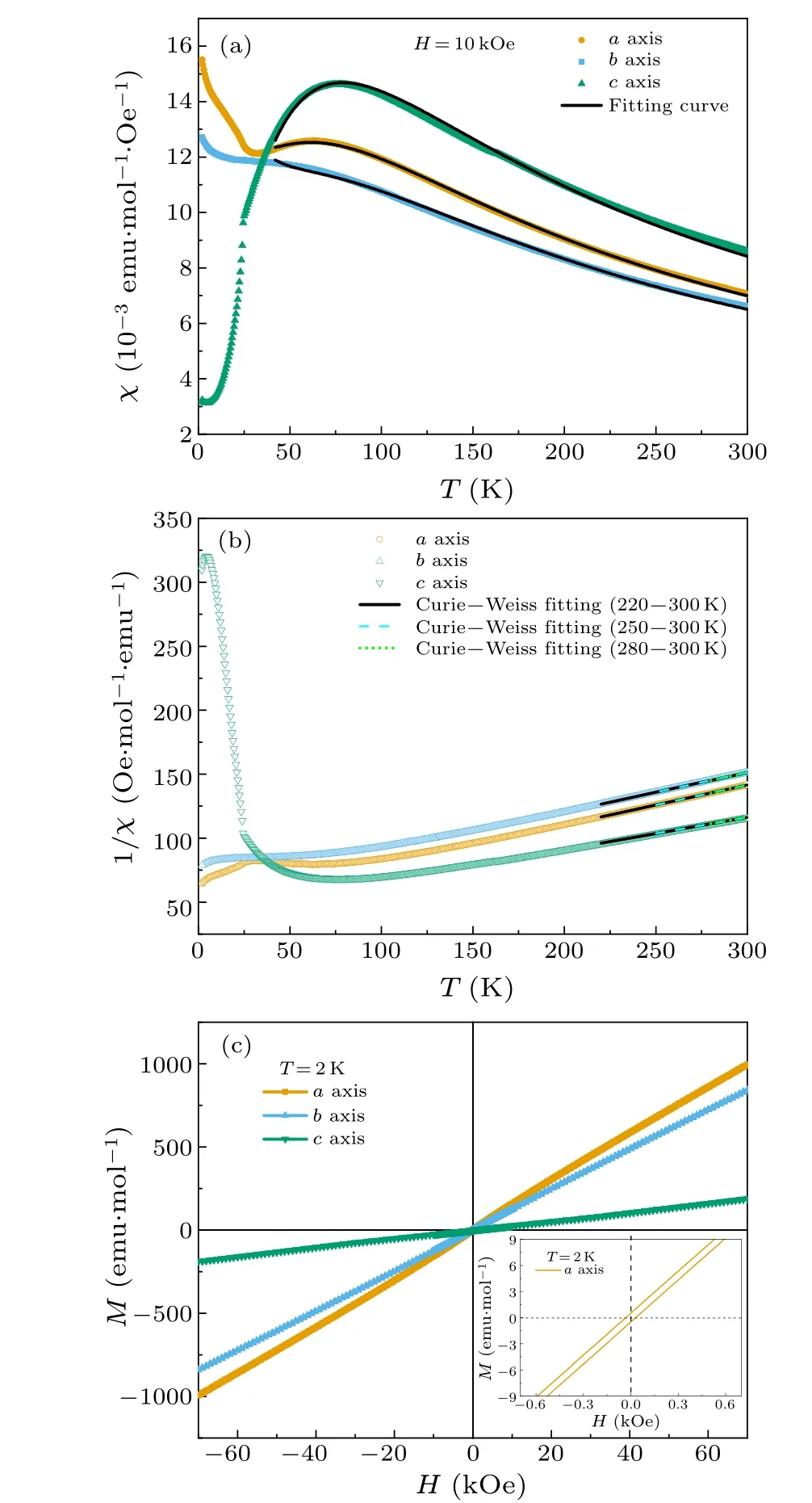
Fig.3.The magnetic measurements of the oriented CoTi2O5 single crystals: (a) χ(T), (b) 1/χ, (c) M(H).Inset in (c) shows the enlarged hysteresis part in the a-axis.
3.3.Magnetization measurements
In Fig.3(a),theχ(T)curve of the CoTi2O5crystal along three major crystallographic axes shows a broad peak at about 80 K, which is a typical sign of the 1D short-range magnetic ordering.A sharp decrease atTN~24 K in theχ(T) along thec-axis of CoTi2O5corresponds to the long-range antiferromagnetic ordering of Co2+.Conversely,belowTN,the magnetic susceptibilities along theaandbaxes increase with decreasing temperature.This apparent anisotropic behavior of theχ(T) curves illustrates that thec-axis is the easy axis in CoTi2O5while the spin chain of Co2+forms along thea-axis,in accordance with the magnetic structure obtained from the neutron diffraction spectra.[18]Theχ(T)curve above 40 K can be well fitted by using the Pade approximation for the Heisenberg spin chain model,[31]as shown in Fig.3(a), indicating that Co2+forms the uniform 1DS=3/2 chain in CoTi2O5.The fitting result gives the value ofg-factor in CoTi2O5along different axes asga~2.45,gb~2.39,andgc~2.67,explaining the difference of the susceptibilities at 300 K.Due to the maximum of the broad peak inχ(T) locates at about 80 K,the 1/χ-Tcurve of CoTi2O5was fitted in multiple intervals above 220 K with the Curie-Weiss law to avoid the influence of short-range magnetic correlation,as shown in Fig.3(b).The obtained effective magnetic moments along thea,b,andcaxes are 5.0(1)µB,5.1(1)µB,and 5.6(1)µB,respectively,which are much larger than the spin-only value of 3.87µBfor the Co2+withS=3/2, indicating that there is a large orbital contribution to the magnetic moment in CoTi2O5.From theM(H)loops at 2 K of all the three axes in Fig.3(c),an obvious magnetic anisotropy can be seen,and the three axes all show an apparent hysteresis behavior with coercive filed around 100 Oe.Both the behaviors ofM(T)andM(H)suggest the appearance of spin-orbit coupling(SOC)in CoTi2O5,which could induce the single-ion anisotropy or the Dzyaloshinskii-Moriya interaction.
However, though the SOC is usually considered to be negligible for systems with 3d transition-metal ions,[32]it can be seen in some materials containing Co2+with a highspin state, e.g., CoNb2O6.[33]The appearance of SOC combined with the octahedral crystal field normally causes Co2+to show an effective spinS=1/2.[34]To further confirm the existence of the SOC in CoTi2O5, the first-principles calculations were performed.To explain the behavior of spin polarization for CoTi2O5in theCmcmphase, the total and partial density of states(DOS)of Ti,Co-3d,and O-2p,are shown in Fig.4.The total DOSs of spin-up and spin-down electrons are similar to each other and conform to the desired antiferromagnetic state.The band gap estimated from Fig.4(a)is about~2.02 eV.The energy region near the Fermi level is mainly composed by the 3d states of Co2+and O-2p states.The energy positions of the O-2p states overlap with those of the Co-3d and Ti-3d states,indicating the hybridization between O-2p and Co, Ti-3d orbitals.The number of unpaired electrons of Co2+is calculated to be 2.72, consistent with the results obtained from the neutron powder diffraction experiments.[18]From the partial DOS of the Co atom in Fig.4(c),the Co2+is in the high spin state 3d7(t52ge2g)withS=3/2.
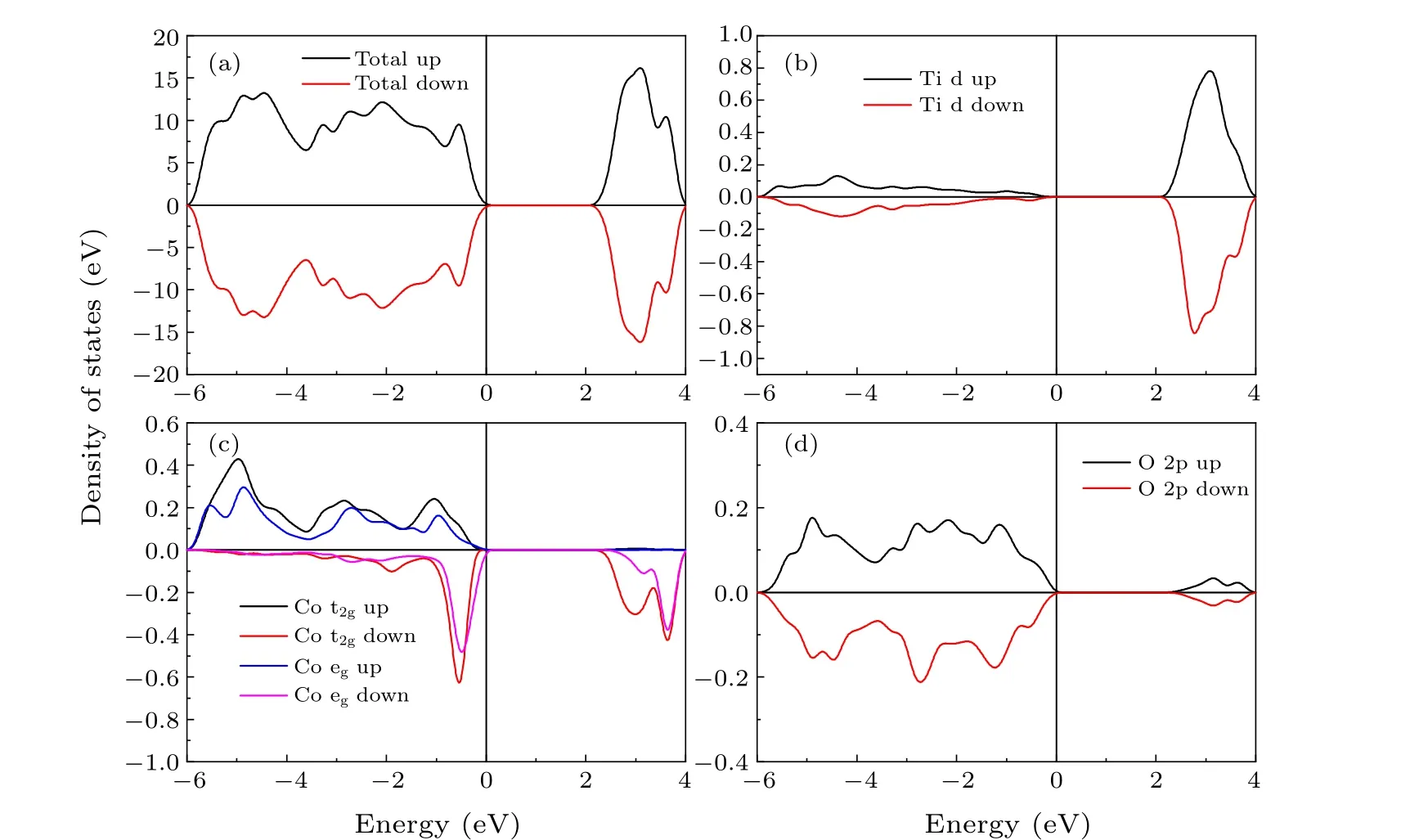
Fig.4.Total and partial density of states for CoTi2O5 within the Cmcm symmetry calculated by GGA+U.(a) The total DOS of CoTi2O5.(b)Partial DOS of d character for Ti.(c)Partial DOS of t2g and eg characters for Co.(d)Partial DOS of 2p character for O.
According to the magnetic propagation vectork=(1/2,1/2,0) in CoTi2O5reported in Ref.[18], we build a 2×2×1 supercell to satisfy the antiferromagnetic structure and consider the SOC to compute the magnetic anisotropy energy(details are given in the supplemental material).The calculation results suggest that,when considering SOC,the total energy of CoTi2O5is about-478.806 eV,which is obviously lower than the-478.540 eV without SOC,confirming the existence of the SOC in CoTi2O5.Since the CoO6octahedron in CoTi2O5is highly distorted,we think that the distorted crystal field of CoTi2O5prevents SOC to reduce the effective spin of Co2+to 1/2,resulting in Co2+with a high-spin state remainingS=3/2 in CoTi2O5.

Fig.5.The thermal expansion coefficient of CoTi2O5 single crystal.Inset shows the magnetostriction effect of CoTi2O5 single crystal at T =3 K.
3.4.Thermal physical properties measurements
The behavior of the phase transition of CoTi2O5was characterized by using specific heat measurements.There is only oneλshaped peak at antiferromagnetic ordering temperatureTN=24 K in the specific heat curve of CoTi2O5, as shown by the black line in Fig.6(a).Kirschneret al.proposed that a spin Jahn-Teller effect occurs atTN, but no experimental evidence was given for any structural distortion.[18]We measured the thermal expansion and magnetostriction of CoTi2O5single crystal,as shown in Fig.5,and found that neither the anomaly of the thermal expansion coefficient aroundTNnor the magnetostriction phenomenon belowTNcan be seen,indicating that there is no strong spin-lattice coupling in CoTi2O5.Therefore,it is reasonable to believe that theλ-shaped peak inC(T)only comes from the antiferromagnetic ordering of CoTi2O5.In the critical region aroundTN, theC(T) curve can be fitted with the following function:[35]
wheret=(T-TN)/TNrepresents the reduced temperature,αis the critical exponent,andA±,B±,F±,andE±are adjustable parameters.Superscripts + and- representT >TNandT <TN,respectively.Within the range of 10-3<|t|<10-1in the vicinity ofTN,the experimental data can be perfectly fitted with Eq.(2), as shown in Fig.6(b).The obtained fitting parameters and critical exponents are listed in Table 1.The values of the critical exponent is obtained to beα+=-0.16 andα-=-0.12, far away fromα=0.11 for the Ising model or theα=-0.01 for theXYmodel,whereas close toα=-0.12 for the Heisenberg model.[36]Although a gapless magnetic ground state is usually expected in a quasi-1D Heisenberg antiferromagnet with half-integer spins,according to the theory of spin waves,[37]the uniaxial magnetic anisotropy in CoTi2O5can open a spin gap in its magnetic excitation spectrum.



Table 1.Adjustable fitting parameters,and critical parameters of the fittings of the specific heat for CoTi2O5.
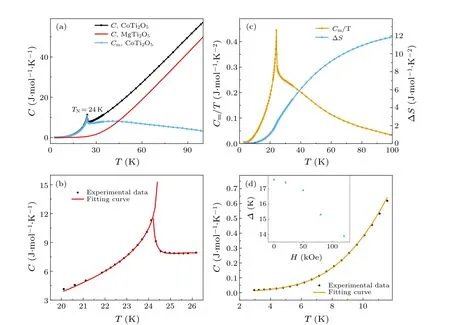
Fig.6.The experimental and fitted specific heat curves of CoTi2O5 single crystal under zero magnetic field.(a)The specific heat of CoTi2O5 and MgTi2O5.The latter is used to subtract the lattice specific heat.(b) The critical behavior fitted from Eq.(2).(c) The magnetic specific heat and change of entropy of CoTi2O5.(d) The low-temperature specific heat data fitted with Eq.(3).The inset shows the magnetic field dependency of Δ,which was also fitted with Eq.(3).
To determine the presence of the spin gap, the specific heat data of CoTi2O5at the low temperature was fitted with Eq.(3),which is extensively used in 1D antiferromagnets,like CuGeO3and NaV2O5,[38,39]to roughly estimate the value of the spin gap:
whereGandQstand for the coefficients,andΔrepresents the value of the spin gap.The fitting result agrees well with the experimental data,as shown in Fig.6(d),and theΔis obtained to be about 17.6 K.The low-temperature specific heat data under different magnetic fields was also fitted with Eq.(3), as shown by the inset in Fig.6(d), illustrating that the value of the spin gap decreases with the increase of the magnetic field.This means that the spin gap in CoTi2O5can be suppressed by the magnetic field.
As a sensitive probe for the scattering of phonon and magnon,[40]the thermal conductivity of the CoTi2O5crystal was also measured to investigate the behavior of the spin gap in CoTi2O5.In Fig.7(a),theκ(T)curve of the CoTi2O5single crystal shows two obvious peaks at about 80 K andT*~12 K when applying the heat flow along the chain direction(a-axis).To figure out the origin of these two peaks, the phonon thermal conductivity (κph) was fitted with the Debye model as follows:[41]

When applying a magnetic field of 90 kOe, the peak atT*inκ(T) is significantly suppressed, as shown in Fig.7(b), while the magnon peak around 80 K is almost field-independent because the short-range magnetic ordering of Co2+cannot be destroyed by the magnetic field.Since the phonon thermal conductivity should be independent of the magnetic field,the weakness ofκ(T)belowTNunder 90 kOe shows that the spin gap tends to be closed by the magnetic field, and then the reappearance of the phonon-magnon scattering results in the suppression of the phonon peak inκ(T)under the strong field.Assuming that phonons at low temperature are scattered only by magnons on the triplet after applying the magnetic field,then the magnetic field dependence ofκphcan be given by Eq.(5), which was successfully used to describe the thermal transport behavior in some quasi-1D antiferromagnets under the low magnetic field,like TlCuCl3and Pb2V3O9:[45,46]
whereaandbare parameters andΔ(H) shows the field dependence of the spin gap.In this case, the spin gap usually changes linearly with the magnetic field and can be written asΔ(H)=Δ(0)+wH,in whichΔ(0)is the value of the spin gap at zero fields andwis a coefficient.[47]The fitting curve overlaps with the experimental data well in low magnetic fields below 40 kOe,as shown by the inset in Fig.7(b),and theΔ(0)is obtained to be about 14.0 K, close to the value of 17.6 K obtained from the specific heat data.The behavior ofκ(H)illustrates that the enhancement of the phonon-magnon scattering process with increasing magnetic field causes the decrease ofκ,proving that the spin gap becomes smaller under the magnetic field.This is consistent with the fitting results of the specific heat shown in the inset of Fig.6(d).

Fig.7.The temperature-dependent thermal conductivity of CoTi2O5 single crystal along the a-axis: (a)κ(T)at zero field,(b)κ(T)at different fields.The inset in (b) shows the field-dependent thermal conductivity at the lowest temperature.
3.5.NMR measurements
To further confirm the existence of a spin gap in CoTi2O5,the59Co nuclear magnetic resonance(NMR)was measured to obtain the spin-lattice relaxation rate 1/T1, which is sensitive to low-energy magnetic excitations and thus gives direct information on the presence of a spin gap (the measured59Co NMR spectra can be seen in the supplemental material).As shown in Fig.8,the temperature dependence of 1/T1is sharply suppressed with decreasing temperature belowTNand shows the activation behavior.By simply fitting with the relationship 1/T1∝exp(-Δ/T), as shown in Fig.8(b), the gap value ofΔ~35 K was obtained, which is the same magnitude as the value roughly estimated from the specific heat data.The exponential decay of 1/T1indicates the opening of a gap in the spin-excitation spectrum of CoTi2O5.
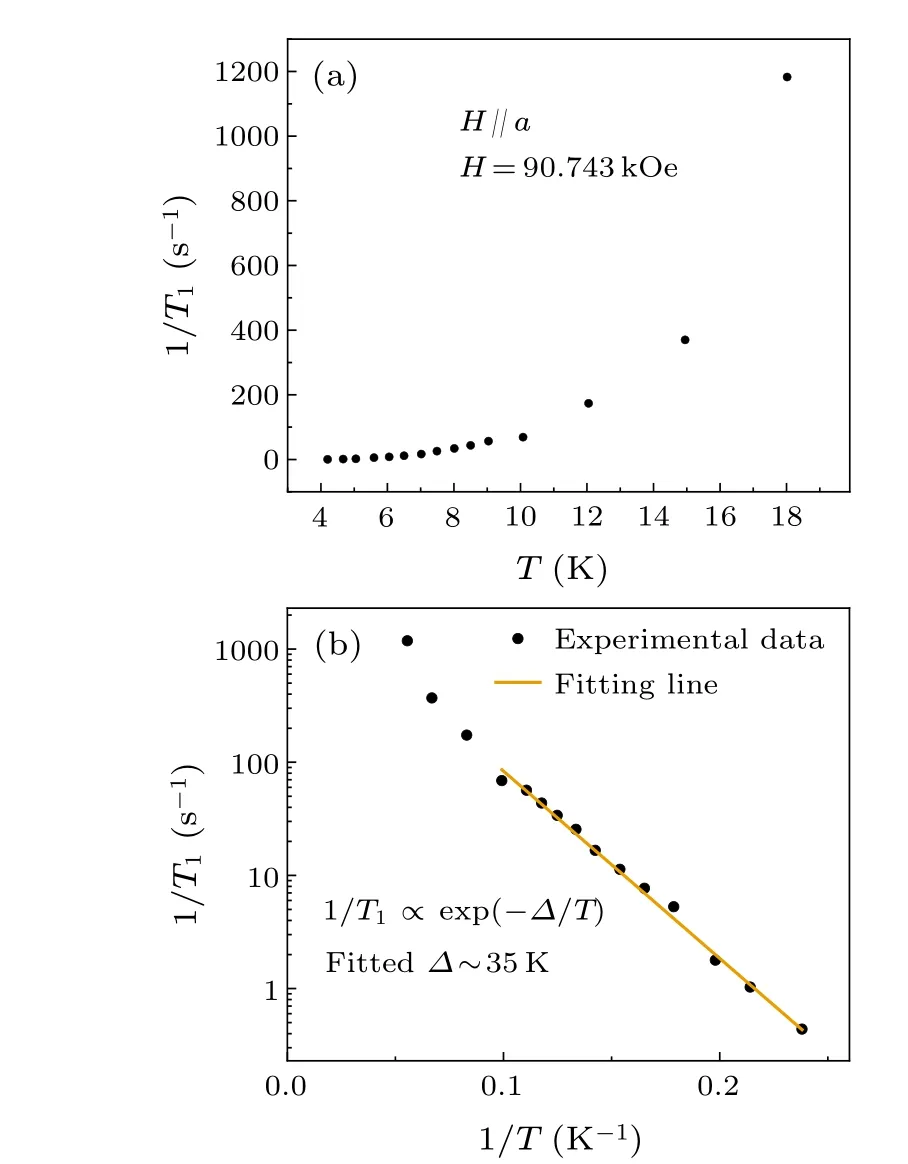
Fig.8.The59Co spin-lattice relaxation rate 1/T1 measured for H//a-axis in CoTi2O5: (a) the temperature dependence of 1/T1, (b) the invertedtemperature dependence of 1/T1 below TN.
4.Conclusion
The pseudobrookite CoTi2O5single crystal with highly ordered Co2+/Ti4+occupation was grown under the pure Ar atmosphere, in which the Co2+forms the uniform 1D spin chain withS= 3/2 and shows a long-range antiferromagnetic ordering atTN=24 K.Both the weak hysteresis behavior inM(H) and first-principles calculations results confirm that there is the SOC in CoTi2O5,which leads to the apparent magnetic anisotropy.A spin gap appears aroundTN, causing the evanishment ofκm, the fast decrease ofCm, and the activation behavior of 1/T1at low temperature.Additionally, the magnetic field can suppress the spin gap and thus enhance the phonon-magnon scattering, and finally results in the weakening of the phonon peak atT*inκ(T).
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No.52372003) and the Funds from Beijing National Laboratory for Condensed Matter Physics.A portion of this work was carried out at the Synergetic Extreme Condition User Facility(SECUF).
- Chinese Physics B的其它文章
- Does the Hartman effect exist in triangular barriers
- Quantum geometric tensor and the topological characterization of the extended Su–Schrieffer–Heeger model
- A lightweight symmetric image encryption cryptosystem in wavelet domain based on an improved sine map
- Effects of drive imbalance on the particle emission from a Bose–Einstein condensate in a one-dimensional lattice
- A new quantum key distribution resource allocation and routing optimization scheme
- Coexistence behavior of asymmetric attractors in hyperbolic-type memristive Hopfield neural network and its application in image encryption

