Winkler地基梁动力学系统的无量纲化与参数识别*

郑罡 曹和生 杜宗松 蔡汶秀 陈鹏

(1. 重庆交通大学 省部共建山区桥梁及隧道工程国家重点实验室,重庆 400074)

(2. 重庆交通大学 土木工程学院,重庆 400074)

引言

Winkler地基梁模型在岩土、公路、铁路以及航空航天等领域都有着广泛的应用[1-4],该模型的受力特点决定其易发生梁体损伤、地基脱空等破坏,从而对结构安全造成严重影响,因此,国内外学者对该模型的损伤诊断问题进行了大量研究,取得了一系列富有成效的进展.文献[5]采用有限元法计算该模型在不同损伤工况下的振型与固有频率,提出基于遗传算法的两级参数识别流程,对梁体损伤位置、程度以及地基脱空位置进行识别;文献[6]通过建立考虑梁内损伤与地基脱空的有限元模型,计算相应工况下的转角模态,并对其进行连续小波变换,识别了梁体损伤与地基脱空位置;文献[7]利用分段函数推导了考虑地基脱空损伤的频率方程,结合共轭迭代算法对地基脱空位置与长度进行识别.

值得注意的是,以上研究均需将各系统参数初始值作为已知量代入计算,若无法对其进行准确识别,则将在一定程度上造成损伤诊断结果与结构实际状态的不符[8,9],因此,其系统参数初始值的识别问题愈发受到研究者的关注,文献[10]通过锤击法实测Winkler地基梁的固有频率,采用传递矩阵法导出以地基刚度为未知数的高次方程,对地基刚度进行识别;文献[9]基于频率响应函数提出针对地基刚度与质量分布的双参数识别算法.值得注意的是,由于Winkler地基梁动力学系统当前未能实现与系统参数的解耦,导致其动力学方程与频率方程仍含多个系统参数,任意系统参数值的变化均将导致求解的重复,使该系统正、反两类求解问题都不具适用于系统参数值任意变化的一般性;更重要的是,该系统的双参数识别反问题也将成为双参数超越方程组的非线性迭代,造成了求解的不便与困难,在一定程度上限制了双参数识别算法的发展与应用.

可以看出,Winkler地基梁动力学系统的参数识别仍然存在有待解决的问题,因此,本文提出基于频率比互等关系的双参数识别算法,旨在同时对该系统两项系统参数进行识别,并实现对其计算的简化.本文首先提出一种新无量纲方法,完成Winkler地基梁动力学系统的无量纲化,实现动力学方程系数的彻底归一化,建立与系统参数解耦的广义频率方程,然后导出频率-梁长预解集与频率比-梁长预解集,利用时间、空间还原系数所建立的线性转换关系提出双参数识别算法,同时对该系统的两项系统参数进行识别.

1 Winkler地基梁动力学系统的无量纲化

据调研,根据无量纲方法的不同,Winkler地基梁动力学系统已演化出三种不同形式:(1)时间、空间坐标均未无量纲化的有量纲动力学系统[11];(2)仅对空间坐标进行无量纲化的部分无量纲动力学系统[12];(3)同时对时间、空间坐标进行无量纲化的完全无量纲动力学系统[13].

不同动力学系统所对应的动力学方程与频率方程(以两端固定边界为例)可分列如下:

(1)有量纲动力学系统

动力学方程:

(1)

频率方程:

(2)

(2)部分无量纲动力学系统

动力学方程:

(3)

频率方程:

1-cos(δ2)cosh(δ2)=0

(4)

(3)完全无量纲动力学系统

动力学方程:

(5)

频率方程:

1-cos(δ3)cosh(δ3)=0

(6)

表1 组合参数计算表

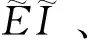
因此,下文提出一种新无量纲方法,以实现Winkler地基梁动力学方程系数的彻底归一化.

1.1 动力学方程的归一化

首先,引入时间、空间还原系数αt、αx,同时对该系统的时间、空间坐标作如下线性变换:

(7)

(8)

将线性变换式(7)、式(8)代入有量纲动力学方程式(1)有:

(9)

(10)

令:

(11)

(12)

解得:

(13)

(14)

当时间、空间还原系数按上式(13)、式(14)取值时,有量纲动力学方程式(1)即可转化为如下归一化形式:

(15)

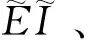
(16)

(17)

(18)

(19)

(20)

(21)

下文对归一化动力学方程式(15)展开求解,导出相应边界条件下的广义频率方程,以得到Winkler地基梁动力学系统的一般解.

1.2 频率方程的广义化

由分离变量法,可设归一化动力学方程式(15)的通解为:

v(x,t)=φ(x)exp(iωt)

(22)

将式(22)代入式(15),可得本征函数φ(x)的通解:

φ(x)=A1cosh(δx)+A2sinh(δx)+

A3cos(δx)+A4sin(δx)

(23)

其中,A1～A4为依赖边界条件与初始条件的复常数;δ系为简化表达而引入的组合参数,可由式(24)计算.

(24)

此处考虑两端固定、两端简支、固定-自由等3种经典边界,相应的边界条件表达式可分列如下:

(1)两端固定

v(x,t)|x=0,l=0

(25)

(2)两端简支

v(x,t)|x=0,l=0

(26)

(3)固定-自由

(27)

将式(22)分别代入边界条件式(25)～式(27),即可得到相应边界条件下的广义频率方程:

(1)两端固定

1-cos(δl)cosh(δl)=0

(28)

(2)两端简支

sinh(δl)sin(δl)=0

(29)

(3)固定-自由

1+cos(δl)cosh(δl)=0

(30)

由式(28)～式(30)可知,以上各边界条件下的广义频率方程均实现了与系统参数的解耦,仅由组合参数δ与无量纲梁长l两个变量决定.结合式(24)通过单变量迭代即可一次性求解得到各阶频率ωi关于无量纲梁长l的预解集,即ωi-l曲线;根据式(21),可进一步得到相应阶次频率比ηij关于无量纲梁长l的预解集,即ηij-l曲线.图1、图2以两端固定边界为例,分别给出了前6阶频率所对应的ωi-l曲线与ηi1-l曲线.

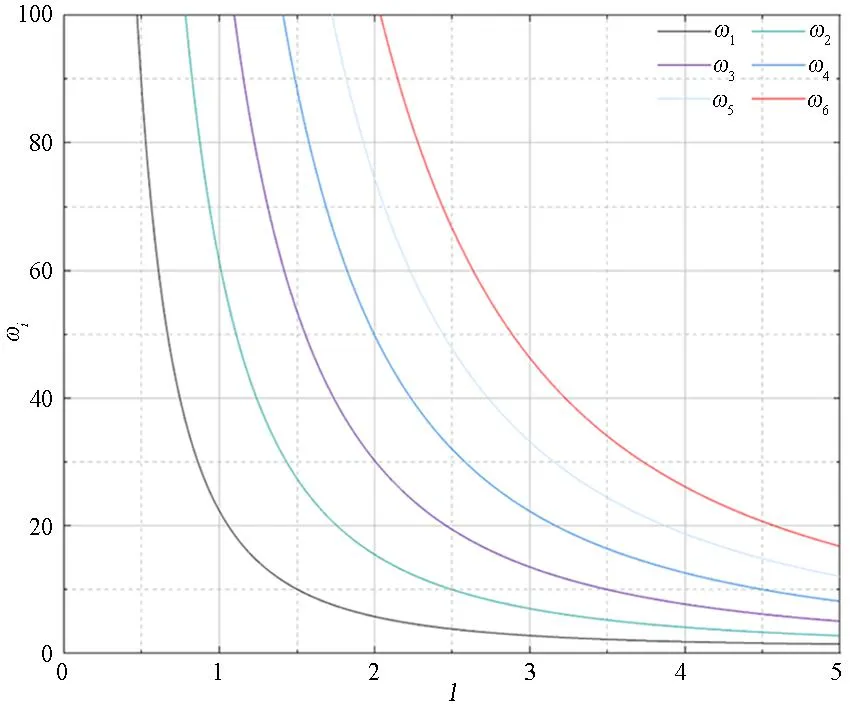
图1 频率-梁长曲线(ωi-l曲线)Fig.1 Frequency-Span curve(ωi-l curve)

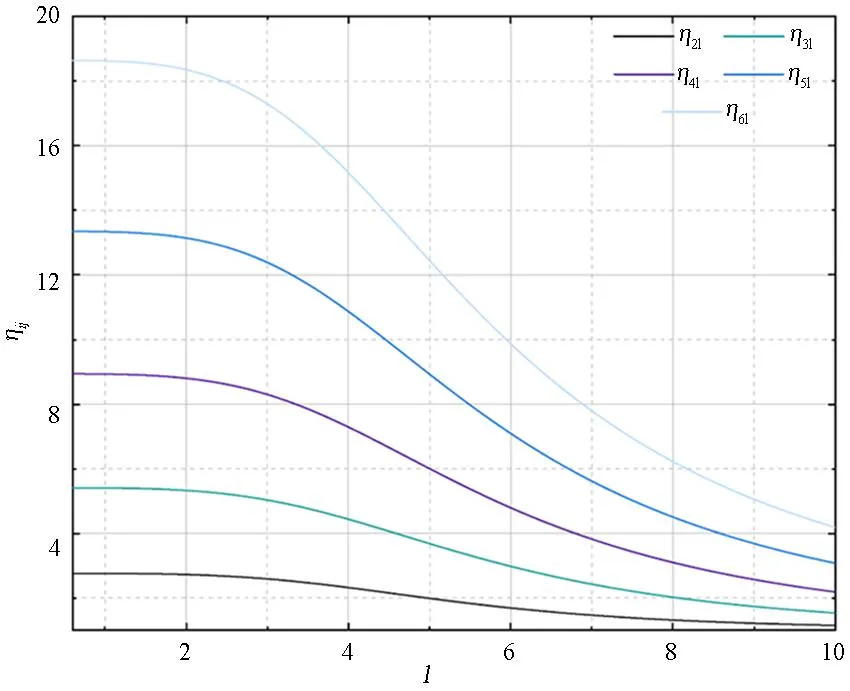
图2 频率比-梁长曲线(ηij-l曲线)Fig.2 Frequency ratio-Span curve(ηij-l curve)

值得注意的是,由于广义频率方程实现了与系统参数的解耦,故频率-梁长曲线、频率比-梁长曲线均具有适用于系统参数值任意变化的一般性,依托于时间、空间还原系数所建立的线性转换关系即可实现对该系统正、反两类问题的定解,不仅可有效避免传统求解方法因系统参数值的改变而导致重复迭代的情况,而且可使传统双参数识别算法中的双参数超越方程组的非线性迭代转换为单参数迭代,使计算得到有效的简化.

基于以上发现,下文提出基于频率比互等关系的双参数识别算法,展开对Winkler地基梁动力学系统的双参数识别.

2 基于频率比互等关系的双参数识别算法

2.1 算法流程

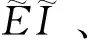
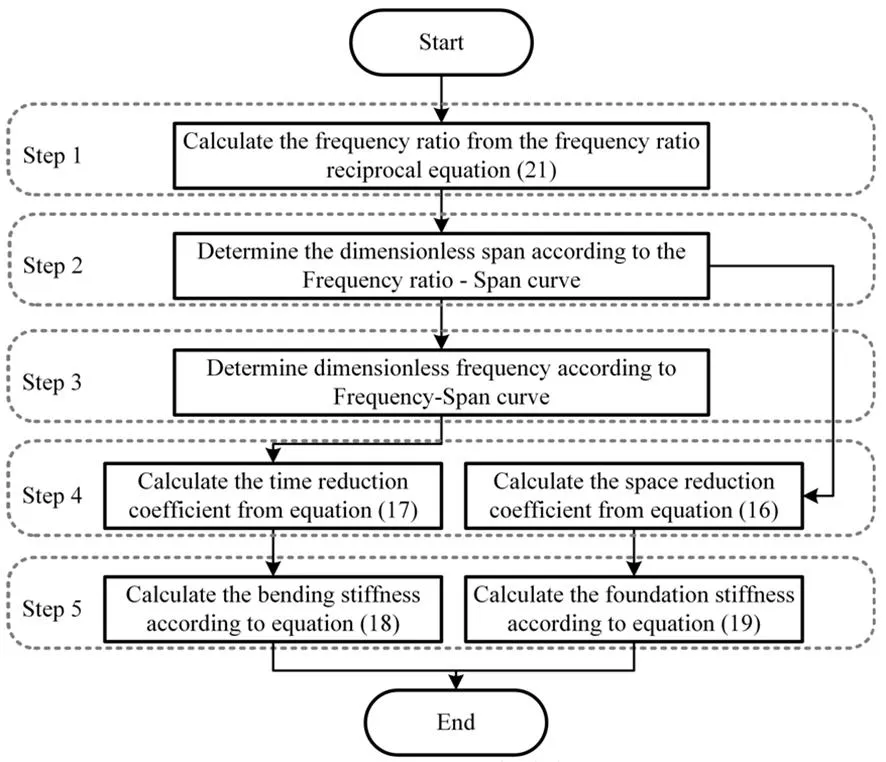
图3 双参数识别算法流程图Fig.3 Flow chart of dual parameter identification algorithm

图3所示算法在准备工作后,可分5步计算.

准备工作:求解广义频率方程,绘制频率-梁长曲线(ωi-l曲线);由频率比互等关系式(21)绘制频率比-梁长曲线(ηij-l曲线).

Step2:由频率比ηij,根据频率比-梁长曲线(ηij-l曲线)确定无量纲梁长l.

Step3:由无量纲梁长l,根据频率-梁长曲线(ω-l曲线)确定各阶次无量纲频率ωi、ωj.

Step4:根据频率转换关系式(17)计算时间还原系数αt;由梁长转换关系式(16)计算空间还原系数αx.

2.2 算法本质

根据2.1节算法流程可知,本文所提出的双参数识别算法,将原本双参数超越方程组的非线性迭代计算问题转化为单变量超越方程(广义频率方程)的求解与式(16)～式(20)所示的线性转换,实现了对双参数识别计算问题的简化,本节旨在探究识别计算得到简化的原因.

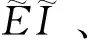
因此,由广义频率方程求解所得到的频率-梁长曲线(ωi-l曲线)其实是适用于系统参数任意变化的预解集,在正问题(频率计算)中,各系统参数值是确定的,可由此直接计算时间、空间还原系数,利用频率-梁长曲线实现对频率的定解.然而,在双参数识别反问题中,在两个系统参数未知的条件下,仅依靠频率-梁长曲线是不够的,但通过式(17),发现了有、无量纲两种体系间所隐含的频率比互等关系式(21),得到频率比-梁长曲线(ηij-l曲线),实现了对动力学系统多模态特性的利用,提出了2.1节所示的算法流程,最终,实现了对双参数识别计算的简化.

3 两类算例

为验证本文无量纲方法与双参数识别算法的可靠性与准确性,下文分别在正、反两类求解问题上,与文献算例进行比对.

3.1 正问题

表2分列了各组算例所采用的系统参数值,表3、表4则给出了在两端固定、两端简支、固定-自由三种边界条件下的计算频率的对比情况.

表2 系统参数表

表3 计算频率对比表系统1

表4 计算频率对比表系统2

值得注意的是,文献[12]以有量纲动力学系统求解、文献[13]以部分无量纲动力学系统求解、文献[14,15]以完全无量纲动力学系统求解,本文则采用新无量纲方法,基于归一化动力学方程与广义频率方程求解.可以看出,在以上各边界条件下,本文计算频率均与文献算例吻合良好,表明本文无量纲方法具有良好的可靠性与准确性.

3.2 反问题

本文以两端固定边界为例,采用系统1相关计算频率对实测频率进行模拟,以研究本文双参数识别算法的稳定性,考虑频率测试的不确定性,现对计算频率施加不同等级随机噪声,模拟实测频率的计算公式可表示如下:

(31)

表5 模拟实测频率表

本文选取0.1%,0.5%两级噪声所对应的模拟实测频率计算各阶频率比ηij,并以不同阶次频率比分别进行识别计算,分析频率比的选择与参数识别误差的关系,研究适于参数识别的最优频率比,频率比的组合方式如表6所示,i、j分别代表分子、分母有(无)量纲频率的阶次.

表6 频率比组合表

利用表6所示的45种频率比分别进行参数识别计算,绘制频率比-识别误差散点图,并对散点进行拟合,分析不同频率比的选择与弯曲刚度、地基刚度识别误差的联系.

由图4、图5可知:(1)弯曲刚度的频率比-识别误差拟合曲线整体平顺,无明显单调性,表明对于弯曲刚度的识别,频率比的选择对其识别精度无明显影响.(2)地基刚度的频率比-识别误差散点呈明显阶梯状分布,相应的拟合曲线也具有明显的单调性,均体现出地基刚度的识别误差随频率比分母频率阶次的增大而增大的趋势,反映出低阶频率对地基刚度的变化更为敏感的特性.

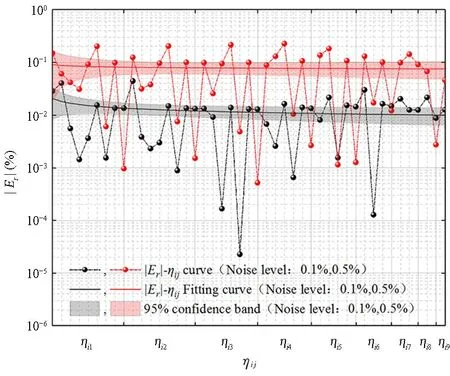
图4 频率比-识别误差曲线(弯曲刚度Fig.4 Frequency ratio-identification error curve

图5 频率比-识别误差曲线(地基刚度Fig.5 Frequency ratio-identification error curve

基于以上发现可知,对Winkler地基梁动力学系统进行参数识别时,应尽量选取低阶频率作为频率比分母频率以提高识别精度.因此,本文选取结构基频作为频率比分母频率,以2～10阶频率作为频率比分子频率,分别以为频率比进行参数识别计算,取9组识别值的平均值作为参数识别最终值.下表7分列了不同噪声等级下弯曲刚度与地基刚度的识别误差.

表7 参数识别误差表

由表7可知,在以上5种不同等级噪声影响下,根据本文参数识别算法,对弯曲刚度的识别误差小于1.21%,对地基刚度的识别误差小于5.47%,本文参数识别算法具有良好的识别精度,可对Winkler地基梁动力学系统的系统参数进行有效识别.

4 结论

为简化Winkler地基梁动力学系统的双参数识别计算,本文提出新无量纲方法,对Winkler地基梁动力学系统进行无量纲化,实现了动力学方程的归一化,得到与系统参数解耦的广义频率方程,在此基础上,建立基于频率比互等关系的双参数识别算法,对该系统的弯曲刚度与地基刚度进行识别,主要研究结论如下:

(1)基于本文所提出的新无量纲方法,该系统的动力学方程与频率方程均实现了与系统参数的解耦,适用于具有任意系统参数值的Winkler地基梁动力学系统.

(2)仅需对广义频率方程进行一次求解即可在相应边界条件下得到频率、频率比关于无量纲梁长的预解集,该预解集具有适用任意系统参数值的一般性,仅需由时间、空间还原系数所建立的线性转换关系即可实现对该系统正、反两类求解问题的定解,避免了传统求解方法因系统参数值的改变而导致重复迭代求解的情况,实现了解的一般化.

(3)本文双参数识别算法的计算仅涉及单变量超越方程的求解与线性变换,避免了传统双参数识别算法中双参数超越方程组的非线性迭代计算,实现了计算的简化.

(4)本文双参数识别算法对弯曲刚度的识别误差小于1.21%,对地基刚度的识别误差小于5.47%,具有良好的识别精度,可对Winkler地基梁动力学系统的系统参数进行有效识别.