第三届跨区域命题征集活动成果展示(三)
本刊编辑部
【深度改编题】
【原题】如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D,点D的坐标为(2,1),求p的值.
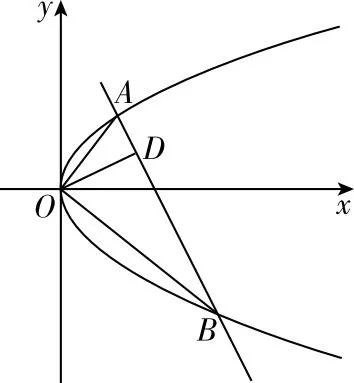

【改编分析】在往年的高考题中有许多题改编于书本,本次改编的试题来源于2019年人教A版教材选择性必修1第146页第10题,在改编过程中涉及的定点定值问题用到了极点极线思想,虽然极点极线的知识我们课本上没有学习,但如果掌握了就可以用它来分析题干,指引我们思考的方向,有了方向再一步步地书写步骤就会较为容易.改编框图如下:



【创新点分析】OA⊥OB这个条件,本质上就是斜率之积为定值时直线AB恒过定点,又由OD⊥AB,创造了一个新的圆,进而考虑到圆上点到圆心距离为定值,从而改编出存在定点Q,使得|DQ|为定值的题目.

(1)证明:P点在一条定直线上;
(2)求△PAB的重心G的轨迹方程.



【创新点分析】对于抛物线方程x2=2py,若P点在一条定直线上运动时,△PAB的重心G的轨迹方程为:4x2-6py-x1x2=0.

在求解过程中,我们涉及消参数法求轨迹问题,可以作为一个新点来做简单练习.
在上述改编题中若把定点D改为焦点,则可以继续研究抛物线中的阿基米德三角形的相关性质.感兴趣的同学可以自己做一下尝试.
【改编3】已知抛物线x2=4y,D(1,2),圆O:x2+y2=r2(r>0)过定点D,圆O与抛物线交于C,M两点,E为劣弧CM上一点,过点E的切线交抛物线于F,G两点,过此两点作抛物线的切线交于点H,求点H到直线FG距离的最大值.
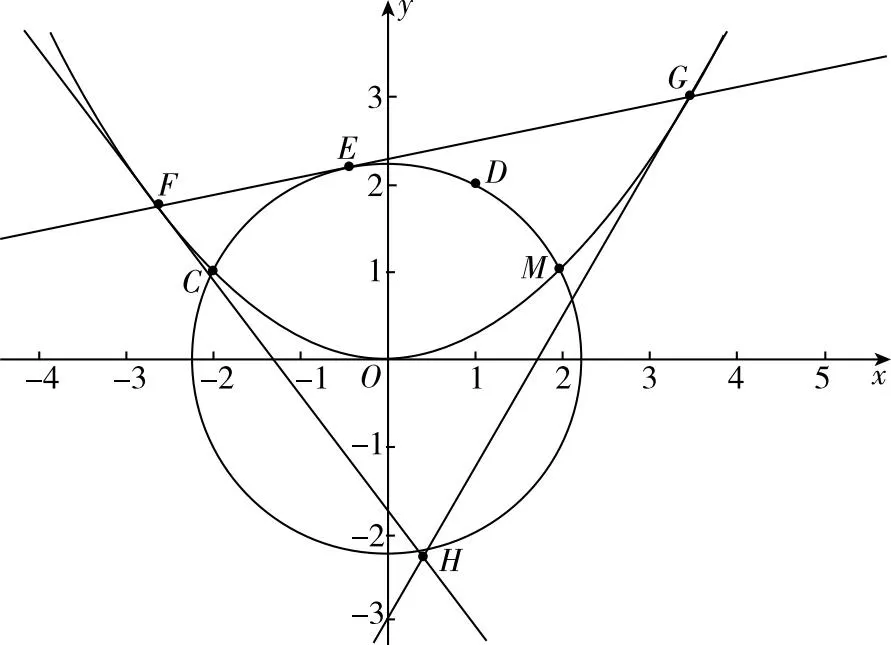
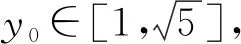
【创新点分析】把圆锥曲线与圆相结合来命题,相对来说较为新颖,当然以前的高考题中已经出现过,只是运算量较大,对于学生运算能力、逻辑思维能力要求较高,本题把E点放在劣弧,限制了E的运转范围,从而为求最值带来了可能.
高三数学复习已进入第二阶段,这是一个将知识连点成线、成网的过程,无论对于学生的知识迁移应用能力,还是对于老师的总结归纳、方法提炼以及合作能力都是一个巨大的挑战,其中课本题的归纳、总结、提炼更是不可或缺的一项.
(改编命题人:黄先锋 安徽省合肥市长丰县第一中学)
【试题评语】这是一道解析几何题,主要考查了逻辑推理能力与数学运算能力.以课本例题为本进行改编,深挖教材,一题多变,层层递进,从抛物线与直线的关系开始,到定点定值问题,再到抛物线与圆的关系,层层递进,设置难度恰当,适合考查学生能力.
(评语老师姓名、单位:魏清泉 青岛市教育科学研究院)
【原创题】

(1)求:轨迹G的方程;
(2)问:直线CD是否恒过定点,若过定点,求出该点坐标;若不过定点,请说明理由.

由题意可知:||MG|-|NG||=||QA|-|QB||=|AB|,∴||MG|-|NG||=4<|MN|.


【思维导图】

思路2:设斜率分别表示出直线AP与直线BP的方程,分别和双曲线方程联立消元,得出关于x的一元二次方程,利用根与系数之间的关系,求出C,D的坐标,根据双曲线的对称性可知定点在x轴上.先利用横坐标相等,特殊化处理,求出点H的坐标(4,0),最后检验kCH=kDH,从而证明直线CD过定点.
【思维导图】


思路3:设出点C(x1,y1),D(x2,y2)的坐标,以及直线CD的方程x=ty+m.先根据直线AC与BD交点在x=1上,求出点P的坐标,建立两根的“非对称”的关系,再把直线CD方程和双曲线方程联立消元,得出关于x的一元二次方程,得出两根的和与积的关系,再代入到非对称关系中化简,求出m的值,从而证明直线CD过定点.
【思维导图】
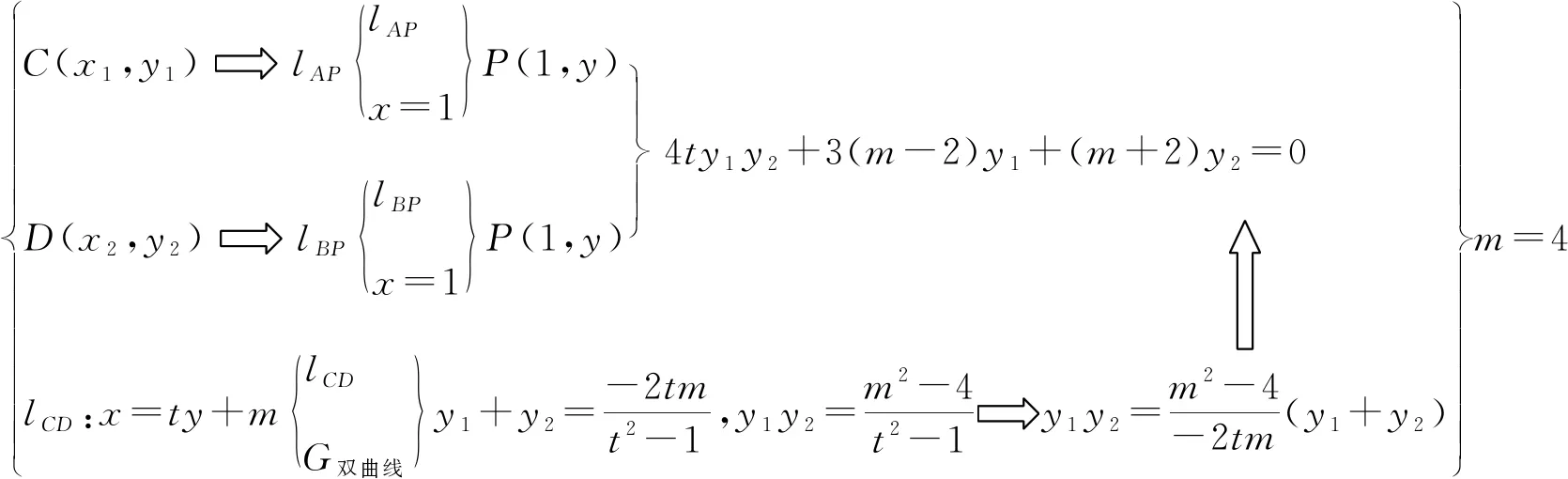

思路4:设出点C(x1,y1),D(x2,y2)的坐标,以及直线CD的方程x=ty+m.先根据直线AC与BD交点在x=1上,求出点P的坐标,建立两根的“非对称”的关系,根据点C在双曲线上,把非对称问题转化为对称处理.再把直线CD方程和双曲线方程联立消元,得出关于x的一元二次方程,利用韦达定理直接带入“对称”关系,求出m的值,从而证明直线CD过定点.
【思维导图】


思路5:设出点C(x1,y1),D(x2,y2)的坐标,以及直线CD的方程x=ty+m.先根据直线AC与BD交点在x=1上,得出3kAC=-kBD,再利用双曲线的第三定义(二级结论)将斜率关系转化为kBD·kBC=-3,得出两根的“对称”关系,再把直线CD方程和双曲线方程联立消元,得出关于x的一元二次方程,利用韦达定理直接代入“对称”关系,求出m的值,从而证明直线CD过定点.
【思维导图】
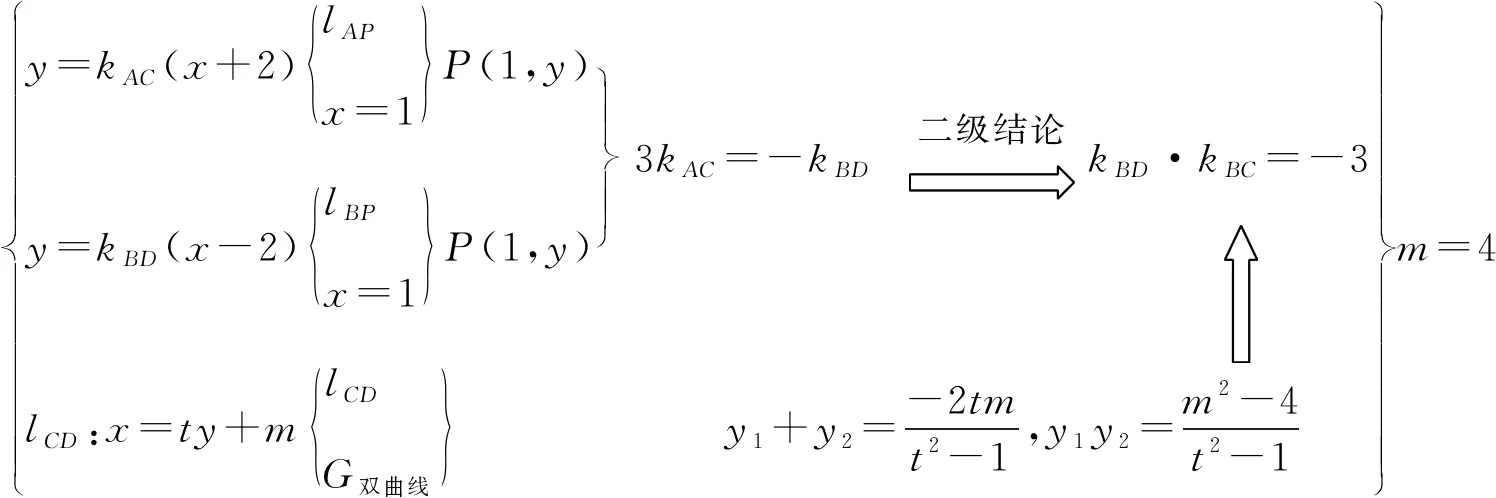

【创新点分析】
1.题干背景选取:题干背景来自课本的探究,知识来源课本,又高于课本.
2.试题考查角度:第(1)小题,是以两圆的位置关系为载体,考查双曲线的定义和标准方程,侧重基本概念的理解,难度不大,面向全体学生;第(2)小题,以直线与直线、直线与双曲线为载体,考查直线是否恒过定点问题,侧重综合知识以及能力的考查,有较好的区分度.
3.试题题型选择:第(1)小题体现知识的融合.第(2)小题选择定点问题考查,有区分度,有难度,有利于选拔人才.
4.试题考查维度:多角度考查基本知识,基本技能,基本思想,关键能力.一是基本概念的考查;二是直线方程的设立;三是直线过定点的知识;四是曲线与曲线的位置关系;五是两根的“非对称”的处理;六是考查数形结合、函数与方程、转化与化归的基本思想;七是考查运算求解、逻辑推理的关键能力.
5.试题设问形式:由易到难,层层递进,入口宽,有深度,让不同的学生得到不同的发展;另外试题具体有开放性,有利于培养学生的探究精神.
【学法指导】涉及直线与(双)曲线问题.
(1)设直线方程通常有两种方法表示:一是设点(坐标)表示,二是设斜率表示.
(2)直线过定点问题通常有两种表示:一是点斜式方程化简,二是利用三点共线.
(3)解决定点问题通常有两种方法:一是先研究特殊后一般,二是直接研究一般情况.
(4)解决定点问题,有时可以先利用(双)曲线的对称性,分析出定点的大致位置,然后设合适的参数,建立直线系或者曲线系方程,如果是两参数,要注意这两个参数之间的相互关系.
(5)涉及直线与(双)曲线相交问题,通常要联立方程组,消元转化为一元二次方程,得出根与系数的关系,然后将目标问题代数化,转化为两根的有关形式,最后代入求解.
(6)对圆锥曲线非对称问题,通常有四种方法化解:一是利用两根关系转化;二是求根公式代入;三是利用曲线方程转化;四是利用二级结论转化.
(7)掌握必要的方法和技巧,如,常用的顺口溜“联立方程解交点,设而不求巧判别,选参建模求轨迹,曲线对称找定点,动点相关归定义,动中求静助解析,非对称曲根转化”等.
【知识延伸】


【易错警示】解析几何中的直线(曲线)与(双)曲线(相交)问题,有时思路清晰,方法自然,但是结果运算不出来.这一方面是运算能力不过关,另一方面是由于方法的选择不适当导致.因此解析几何的问题,首先要用几何眼光观察,即先利用几何的相关性质转化,再用代数知识表示几何问题,然后进行代数运算.
【高考风向】解析几何是每年高考的必考内容与重点内容,是考查学生关键能力和学科素养的重要载体.高考对解析几何的考查一般以课程学习情境与探索创新情境为主,注重数学知识的基础性、综合性和应用性以及创新性与选拔性的考查,具体呈现以下规律.
(1)基础性:高考通过对直线、圆与圆锥曲线的基本概念、简单几何性质以及位置关系的考查,考查考生逻辑思维能力和运算求解能力等,从而促进学科素养的提升,提高考生从数学角度发现问题和提出问题、分析问题和解决问题的能力.
(2)综合性与应用性:解析几何涉及知识点众多,高考通过综合设计试题,将多个知识点衔接起来.如,与平面向量、三角函数、导数、不等式等学科内容进行考查.这就要求考生从整体上把握各种现象的本质和规律,能综合应用所学知识、原理和方法来分析和解决问题.
(3)创新性与选拔性:理性思维的高层次表现就是创新意识的呈现.在高考数学中,对解析几何的考查充分考虑学科特点,通过提出有跨度和有挑战的问题,创设新颖的试题情境,创新试题呈现方式,增强试题的开放性和探究性等途径,引导考生深度思考和自主探究,展现考生分析问题和解决问题的思维过程,考查考生独立思考、创新能力、批判性思维能力,以及考查学生应用数学与探索数学的素养,体现选拔功能.
(原创命题人:吴文明 安徽省合肥北城中学)
【试题评语】本题是数学探究情境,考查的学科素养是理性思维和数学探索,利用圆与圆的位置关系,考查双曲线的定义与标准方程、直线与双曲线的位置关系、直线过定点问题,考查逻辑思维能力和运算求解能力,难度较大.
(评语老师姓名、单位:魏清泉 青岛市教育科学研究院)

