分数阶微分方程耦合系统边值问题正解的存在性
申腾飞
(中国矿业大学 理学院,江苏 徐州 221116)
分数阶微分方程耦合系统边值问题正解的存在性
申腾飞
(中国矿业大学 理学院,江苏 徐州 221116)
首先利用Leray-Schauder非线性抉择和锥拉伸与压缩不动点定理等,讨论了一类非线性的Riemann-Liouville分数阶微分方程耦合系统边值问题,得出边值问题的正解存在的充分条件。其次,结合积分方程与微分方程解的等价性及范数性质给出正解不存在的几个充分条件。
分数阶微分方程;边值问题;不动点定理;正解
0 引言
近年来分数阶微分方程问题得到了广泛的关注,一方面是分数积分及微分本身的发展;另一方面是其在物理、化学、力学等领域的应用[1]。近年来越来越多的学者进行分数阶微分方程的研究[2-10]。文献[2]讨论了一类分数阶微分方程两点边值问题
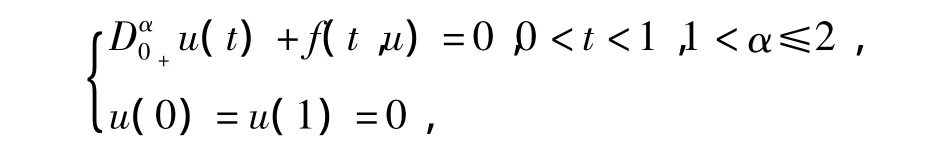
正解的存在性;文献[10]研究一类分数阶微分方程耦合系统边值问题

正解的存在性;文献[4]利用锥拉伸与锥压缩不动点理论讨论了含参数的分数阶两点边值问题的正解的存在与不存在性;文献[5]研究了带有p-Laplacain算子三点的边值问题。笔者将采用几类不动点定理进一步研究一类分数阶微分方程耦合边值问题。
文中主要探讨下面分数阶微分方程的边值问题

1 预备知识



引理6 若 f,g:[0,1]×[0,+∞)→[0,+∞)连续函数,则(u,v)是系统(1)的解当且仅当它是系统(2)的解。
证明过程类似于文献[10],在此省略。
引理7 设D是Banach空间X的一个非空闭子集,而T是D到其自身内的映像,它在D内满足Lipschitz条件,即对任意的 x,y∈D,有
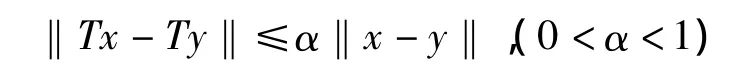
(这里的α称为Lipschitz常数),则必存在唯一x*∈D,使Tx*=x*,即T有且只有一个不动点。
引理8(Leray-Schauder非线性抉择) 假设Ω是Banach空间X上的凸集K的一个相对子集,令T:¯Ω→K 是紧的且 0∈Ω,则
(Ⅱ)存在一个点 u∈∂Ω 和 λ∈(0,1),使得u=λTu。

2 主要结果


容易证明T(P)⊂P是一致有界的,且等度连续的。此过程类似于文献[2]中的方法,故略。综上T是一致有界的又是等度连续的,由Arzela-Ascoli定理知T(P)是相对列紧的,故T是全连续的。
为了叙述方便,定义如下常数:

定理1 设 f,g:[0,1]×[0,+∞)→[0,+∞)连续函数,若存在函数k(t),l(t)∈C(I)使得对任意的(t,u),(t,v)∈[0,1]×[0,+∞],若满足

则问题(1)存在唯一的正解。

又因为T1,T2为压缩映射,所以此时T:p→p是压缩映射,由引理7得到必存在唯一的不动点 (u,v)∈p,函数(u,v)就是问题(1)的唯一正解。
定理2 设 f,g:[0,1]×[0,+∞)→[0,+∞)连续函数,若存在非负不减的连续函数 φ,ψ:[0,+∞)→[0,+∞),满足


同理,‖u‖<‖u‖。
由于‖(u,v)‖=max{‖u‖,‖v‖}<‖(u,v)‖,得出矛盾,故结论得证。
定理5 若 B1f(t,v(t))>v(t),B2g(t,u(t))>u(t),∀(u,v)∈P 成立,则问题(1)无解。
证明 假设(u,v)是问题的一个解,则

同理可得‖u‖>‖u‖。
由于,‖(u,v)‖ =max{‖u‖,‖v‖}> ‖(u,v)‖,得出矛盾,故结论得证。
[1]KILBAS A A,SRIVASTAVA H M,TRUJILLO J J.Theory and applications of fractional differential equations[M].Amsterdam:Elsevier,2006.
[2]BAI ZHANBING,LÜ HAISHEN.Positive solutions for boundary value problem of nonlinear fractional differential equation[J].J Math Anal Appl,2005,311(2):495-505.
[3]GAN SI QING.Dissipativity of θ-methods for nonlinear volterra delay-integro-differential equations[J].J Comput Appl Math,2007,206(2):898-907.
[4] SUN HONGRUI,TANG LUTIAN,WANG YINGHAI.Eigenvalue problem for p-laplacain three-point boundary value problems on time scales[J].J Math Anal Appl,2007,331:248-262.
[5]ZHANG SHUQIN.Positive solutions for boundary-value problems of nonlinear fractional differential equations[J].Electronic Journal of Differential Equations,2006,2006(36):1-12.
[6]ZHANG SHUQIN.Existence of positive solution for some class of nonlinear fractional differential equations[J].J Math Anal Appl,2003,278(1):136-148.
[7] XU XIAOJIE,JANG DAQING,YUAN CHENGJUN.Multiple positive solutions for the boundary value problem of a nonlinear fractional differential equation[J].Nonlinear Analysis:Theory,Methods& Applications,2009,71(10):4676-4688.
[8]BAI ZHANBING.On positive solutions of a nonlocal fractional boundary value problem[J].Nonlinear Analysis:Theory,Methods& Applications,2010,72(2):916-924.
[9]SALEM H A H.On the fractional m-point boundary value problem in reflexive banach space and weak topologies[J].J Comput Appl Math,2009,224(2):565-572.
[10]苏新卫.分数阶微分方程耦合系统边值问题解的存在性[J].工程数学学报,2009,26(1):133-137.
Existence of positive solutions for boundary value problem of coupled system of fractional differential equations
SHEN Tengfei
(College of Sciences,China Univeisity Mining& Technology,Xuzhou 221116,China)
This paper introduces an investigation into the existence and nonexistence of positive solutions for boundary value problem of a coupled system of nonlinear fractional differential equations and features some results of existence and nonexistence positive solutions for boundary value problem obtained by using the fixed point theorem.
fractional differential equation;boundary value problem;fixed point theorem;positive solutions
O175.8
A
1671-0118(2012)01-0098-04
2012-01-13
申腾飞(1987-),男,安徽省蚌埠人,硕士,研究方向:微分方程,E-mail:114950809@qq.com。
(编辑 晁晓筠)

