一类具有收获率互惠系统的稳定性及Hopf分岔*
陈红兵
(天水师范学院数学与统计学院,甘肃 天水 741001)
文献[1]研究了具有HollingⅡ功能反应的模型
其中x(t)为食饵,y(t)为捕食者,a,b,c,d,e,f为常数。a,d表示食饵和捕食者的固有增长率,b,e表示种群的种内竞争系数,c表示捕食者的捕获能力,f表示食饵对捕食者的供养能力。
本文我们研究具有时滞的HollingⅡ功能反应模型
(1)
其中x1(t)和x2(t)为两种群在t时刻的密度,a1,a2为食饵和捕食者的固有增长率,b1,b2为环境制约系数,c1和c2为两种群的相互转化系数,d1和d2为捕获强度。并且a1,a2,b1,b2,c1,c2,d1,d2为正常数。
文献[2-5]研究有关捕食系统的稳定性和时滞的Hopf分岔,但关于互惠系统时滞的Hopf分岔并不多见,本文我们在参考文献[6-9]理论的基础上研究互惠系统时滞的Hopf分岔及分岔的稳定性。
1 有界性
(H1)b2>c2,
φ1(0)≥0,φ2(0)≥0
(2)
引理1 系统 (1) 存在满足初值(2)的正解。
x1(t)>0,x2(t)>0显然成立。
引理2 系统(1)满足初值(2)的解为一致有界的。
证明
(3)
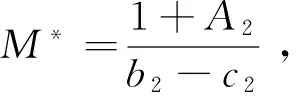

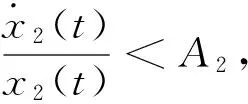
同理得x1(t)有界。
2 Hopf 分岔的存在性
在本文假设A1>0,和A2>0。
(H2)A2c1>A1c2,
(H3)c1>c2,
其中A1=a1-d1,A2=a2-d2,σ=A1b2+A2c1-b1b2-A1c2为常数。
引理3 如果假设(H1)和(H2)成立,则E*为系统(1)的正平衡点。
系统(1)平衡点的特征方程为
λ2+Ae-λτλ-Bλ+Ce-2λτ-De-λτ=0
(4)
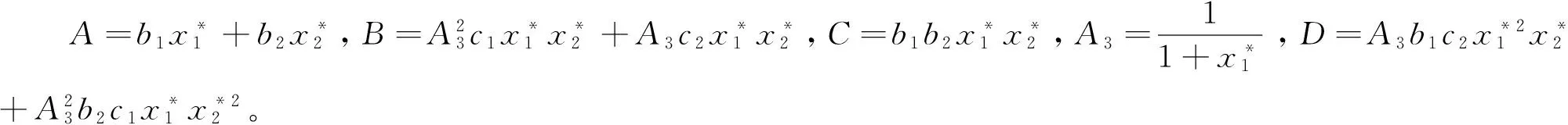
定理1 当τ=0系统(1)满足假设条件(H2)的平衡点E*是稳定的。
证明当τ=0时,系统(1)平衡点特征方程为
λ2+(A-B)λ+C-D=0
(5)
其中
即特征方程(5)有两个负实部的根,所以系统(1)的平衡点E*是稳定的。
引理4[2]对如下多项式
P(λ,e-λτ1,…,e-λτm)=
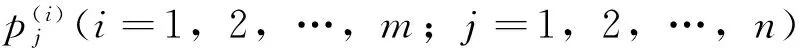
定理2 假设系统(1)满足条件(H3)和(H4),则
(i) 当τ∈[0,τ0)时,系统(1)的正平衡点E*是全局渐近稳定的(τ0如下);
(ii) 当τ=τ0时,系统(1)的正平衡点E*出现Hopf分支岔(τ0如下)。
证明令λ=iω代入式(4),并分离实部和虚部得
(6)
(6)式与下式同解
ω8+B1ω6+B2ω4+B3ω2+B4=0
(7)
其中B1=2B2-A2,B2=B4-2C2+2A2C-A2B-D2,
B3=2B2C2+A2C2+B2D2+2CD2-4ABCD,B4=C4-C2D2,
令η=ω2,则(7)式变为
η4+B1η3+B2η2+B3η+B4=0
(8)
令F(η)=η4+B1η3+B2η2+B3η+B4,显然
F(C)=-(2D-AB)2C2-B2C(D2-B2C)=
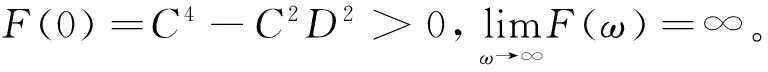

下面把τ0和ω0代入(4)式,求

f2(ω0) = (2Ccosω0τ0-D)2+(Aω0-2Csinω0τ0)2
而
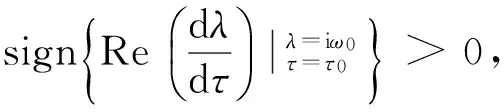
3 Hopf 分岔与分岔周期解的计算公式
下面用中心流行定理和规范型方法给出系统(1)的分岔方向, 分岔周期解及稳定性的计算公式。
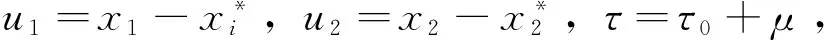
(9)
其中u(t)=(u1(t),u2(t))∈R2,L:C→R2,F:R×C→R2,则有
Fμ(φ)=(τ0+μ)·

(10)
F(μ,φ)=
(11)
由Riesz定理可得,一定存在有界变差函数的矩阵η(θ,μ),使得
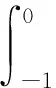
(12)
其中η(θ,μ):C→R2,θ∈[-1,0],令
其中φ∈C([-1,0],R2)。取

则系统(9)可写成算子方程
(13)
其中u=(u1,u2)T,ut(θ)=u(t+θ),θ∈[-1,0],μ=τ-τ0。由定理2可知,当μ=0时系统(13)可能产生Hopf分支。
定义算子A*(μ)为
并且定义双线性内积为
(14)
其中ψ∈([0,1],R2*),η(θ)=η(θ,0)。
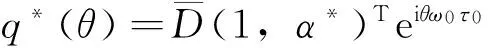
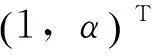
由(14)式可得
令

定义
ut(θ)-2Re{v(t)q(θ)}
(15)
由中心流行定理可得
(16)
当W是实数时ut也是实数,因此下面只考虑实数ut,并且有
〈A*(0)q*,ut〉+〈q*,R(0)ut〉=
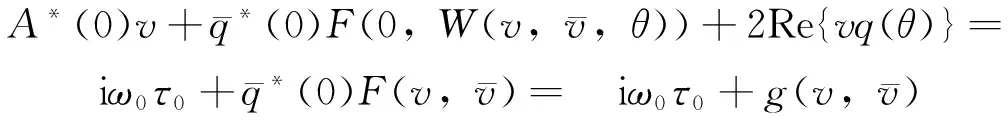
其中
(18)
则由(15)式和(16)式可得
又因为q(θ)=(1,α)Teiθω0τ0,所以有下式成立。
由F(μ,ut)得
所以可得
因为
A(0)ut+R(0)ut+2Re{gq}=
(19)
其中
(20)
所以得
(21)
由(19)式得
(22)
(23)
所以有
(24)
即
(25)
(26)
由A的定义和(21)式可得

(27)
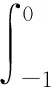
(28)
所以有
则可求得E1和E2。
令
β2=2Re{c1(0)},
(29)
定理3 系统(1)的分岔方向由μ2确定,当μ2>0(μ2<0),Hopf分岔是上临界的(下临界的),即当τ>τ0(τ<τ0)存在相应的Hopf周期解;分岔周期解的稳定性由β2确定,当β2<0(β2>0)分岔周期解稳定(不稳定);分岔周期解的周期由T2确定,当T2>0 (T2<0) 周期增加(减少)。
4 举例
(30)
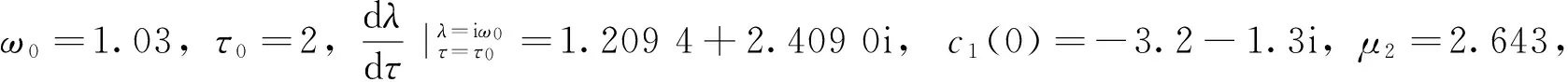
β2=-6.4,T2=2.419 4。 见图 1和图 2 。
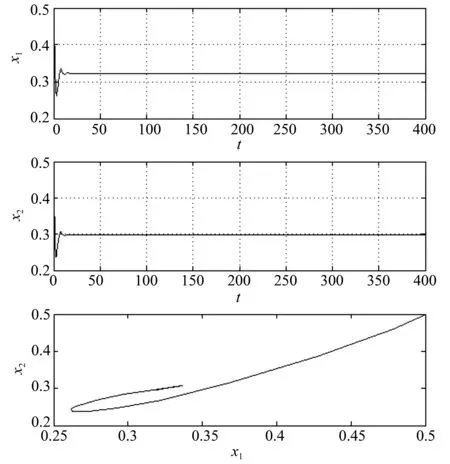
图1 τ=1.2平衡点渐近稳定Fig.1 The positive equilibrium is stabled for τ=1.2

图2 τ=2.1 Hopf 分岔及周期解稳定Fig.2 Hopf bifurcation and stability for τ=2.1
参考文献:
[1] LI Y Q, GAO H L. Existence, uniqueness and global asymptotic stability of positive solutions of a predator-prey system with Holling II functional response with random
perturbation [J]. Nonlinear Analysis, 2008, 68: 1694-1705.
[2] RUAN S, WEI J. On the zeros of transcendental functions with applications to stability of delay differential equations with two delays [J]. Dyn Contin Discrete Impuls Syst Ser A Math Anal, 2003, 10:863-874.
[3] YAN X P, LI W T. Hopf bifurcation and global periodic solutions in a delayed predator-prey system [J]. Appl Math Comput, 2006, 177:427-445.
[4] FARIA T. Stability and bifurcation for a delayed predator-prey model and the effect of diffusion [J]. J Math Appl, 2001, 254:433-463.
[5] SONG Y L, WEI J J. Local Hopf bifurcation and global periodic solutions in a delayed predator-prey system [J]. J Math Appl, 2005, 301:1-21.
[6] HASSARD B, KAZARINOFF D, WAN Y. Theory and applications of Hopf bifurcation [M]. Cambridge: Cambridge University Press, 1981.
[7] QIN Y, WANG L, LIU Y, et al. Stability of the dynamics systems [M]. Beijing: Science Press; 1989.
[8] HALE J, LUNEL S M. Introduction to functional differential equations [M]. New York: Springer-Verlag, 1993.
[9] STECH A. Hopf bifurcation calculations for functional differential equations [J]. J Math Anal Appl, 1985, 109:472-491.

