上的Wiener-Hopf算子*
谢佩珠,曹广福
(广州大学数学与信息科学学院∥数学与交叉科学广东普通高校重点实验室,广东 广州 510006)
实空间上的Wiener-Hopf算子有两种定义方法。一种定义是

其中Lp(R+)表示R+上的Lp空间,m(a)表示乘积算子,P是从Lp(R)到Lp(R+)的投影算子。关于该算子的详细定义及性质可见文献[1, 第9章]。另外一种定义是

其中Hp(R)表示R上的Hardy空间,P表示从Lp到Hp的投影算子。Wiener-Hopf算子包含了很多重要的积分算子,曾有很多学者研究,见文献[1-6]。
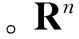
1 概念
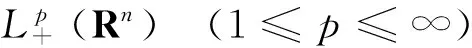
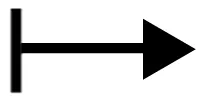
显然, 对所有的1≤p≤∞,该算子都是有界的。





若a∈L∞(Rn),则算子
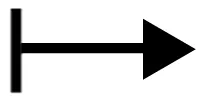
有界且其范数为‖a‖L∞。令Mp(Rn) (1≤p<∞)表示所有满足以下性质的a∈L∞(Rn)所组成的集合:若φ∈L2(Rn)∩Lp(Rn),则M(a)φ∈Lp(Rn)且存在不依赖于φ的常数Cp使得‖M(a)φ‖Lp≤Cp‖φ‖Lp。

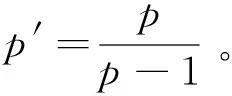

(ii)M2(Rn)=L∞(Rn);

(iv)Mp(Rn)=Mp′(Rn),且若a∈Mp(Rn),则‖M(a)‖=‖M(a)‖;
(v)Mp(Rn)在范数‖a‖Mp(Rn)= ‖M(a)‖下为Banach代数;



M(a)φ(x)=cφ(x)+k*φ(x)(x∈Rn)
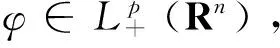
W(a)φ(x)=cφ(x)+k*φ(x),
(x=(x1,…xn)∈Rn,xn>0)
(ii) 对δ∈Rn,定义ωδ∈L∞(Rn)为ωδ(x)=e-2πiδ·x。 则对所有的p:1≤p<∞,有ωδ∈Mp(Rn)且若φ∈Lp(Rn),
M(ωδ)φ(x)=φ(x-δ) (x∈Rn)
对

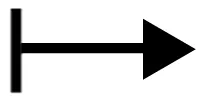
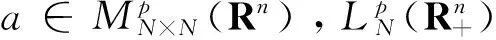
定义3 设X和Y为Banach代数。如果存在常数γ>0使得
‖Y
对任意有限个ajk∈X都成立,则称映射i:X→Y为次可乘的。满足(1)式的次可乘算子i称为γ-次可乘。
2 Wiener-Hopf算子的性质
在本节中,我们研究Wiener-Hopf算子的性质。
命题1 若1≤p<∞,则映射
是1次可乘的同构映射。
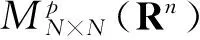
可见W是1次可乘的。由
‖W(a)‖≥‖M(a)‖≥‖W(a)‖

记‖A‖Φ(X)为算子A的本征范数,即
‖A‖Φ(X)=inf{‖A+K‖:K∈C∞(X)}
其中C∞(X)为空间X上紧算子全体构成的空间。

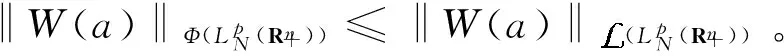
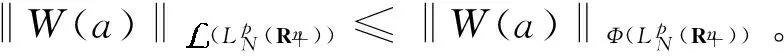

⟺M(a)∈G⟺
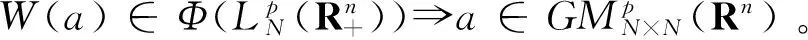
证明 设A∈为M(a)的逆算子。在等式M(a)τv=τvM(a)两边同时乘以A可得τvA=Aτv,即A是平移不变算子。因此,存在使得A=M(b)。不难验证ab=ba=I。故而,当M(a)可逆时


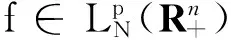
由此可得
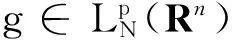
其中Q=I-P。设v=(0,…,vn)。进一步
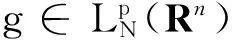

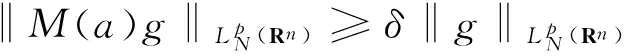
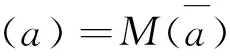


Hankel算子和Wiener-Hopf算子之间的关系是研究Wiener-Hopf的交换子的关键。若a,b∈Mp(Rn),则
W(ab) =PM(ab)P=PM(a)(P2+QJJQ)M(b)P=
PM(a)PPM(b)P+PM(a)QJJQM(b)P=
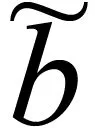

H(a)φ(x)=
(x=(x′,xn)∈Rn,xn>0);

(x=(x′,xn)∈Rn,xn>0)

注2 类似地,可以定义空间Rn-i×(R+)i,1≤i≤n上的Wiener-Hopf算子和Hankel算子。注意到当k∈L1(R)时,算子

参考文献:
[1] BOTTCHER A, SILBERMANN B. Analysis of Toeplitz operators [M]. Berlin: Springer-Verlag, 1990.
[2] ALLDRIDGE A, JOHANSEN T. Spectrum and analytical indices of the C*-algebra of Wiener-Hopf operators [J]. J Funct Anal, 2007, 249: 425-453.
[3] COBURN L, DOUGLAS R. Translation operators on the half-line [J]. Proc Nat Acad Sci USA, 1969, 62: 1010-1013.
[4] GOHBERG I, KREIN M. Systems of integral equations on the half-line with kernels depending on the difference of the arguments [J]. Amer Math Soc Transl, 1960, 14: 217-287.
[5] KREIN M. Integral equations on the half-line with a kernel depending on the difference of the arguments [J]. Amer Math Soc Transl, 1962, 22: 163-288.
[6] XIA J. Wiener-Hopf operators with piecewise continuous almost periodic symbol [J]. J Operator Theory, 1985, 14: 147-171.
[7] AJMI H. Harmonic Bloch functions on the upper half-space [D]. Michigan State University, Ph D Thesis, 1992.
[8] CHOE B, KOO H, NAM K. Finite rank product theorems for Toeplitz operators on the half-space [J]. J Math Soc Japan, 2009, 61: 885-919.
[9] CHOE B, KOO H, YI H. Gleason’s problem for harmonic Begman and Bloch functions on half-spaces [J]. Integr Equ Oper Theory, 2000, 36: 269-287.
[10] RAMEY W, YI H. Harmonic Bergman functions on half-spaces [J]. Trans Amer Math Soc, 1996, 348: 633-660.
[11] HORMANDER L. Estimates for translation invariant operators inLpspaces [J]. Acta Math, 1960, 104: 93-140.

