意外生成 精彩探究——一堂拓展训练课上的意外探究

☉江苏省苏州市吴县中学 吴海燕

在我们平时的教学中，常会遇到这样的情形，原本一堂风平浪静的课，却由于学生的一个提问改变了教师的预设，将我们的课堂教学引向未知的方向.其实，当我们教师面对此种情形时，如能从尊重学生的需要出发，顺势将生成进行到底，往往会收到意想不到的教学效果.笔者就曾有过多次这样的体验，现将一次体验介绍给大家，并谈谈一些认识，供同仁们赏析.

一、课例展示

这本是为部分高一优秀学生所上的一堂拓展训练课，课题为《函数奇偶性与单调性应用》，首先笔者与学生们一起回忆了函数奇偶性与单调性的有关概念，接下来出示了下面一道题：

（出示该题，意在提醒学生：涉及函数奇偶性的问题，必须先考虑函数定义域.没想到，题目一出现，就立即引起了“轰动”，答案k=1的声音占了主流.）

这是一道隐蔽性极强的题目，大多数学生认为该函数的定义域是R，从而误入歧途.解铃还须系铃人，笔者请一位答错的同学来回答一下他是怎样得到该结果的.

生 1：因为函数f（x）是奇函数，所以f（0）=0，由此得k=1.

师：你这样解，思维严谨吗？

生1：我认为这方法很巧，没觉得有不严谨的地方.

（教室里面发出笑声，有一位学生立即站起来反驳.）

生2：题目说f（x）在定义域上为奇函数，又没说0一定在其定义域内，所以不能利用f（0）=0这一结论.

生1：有道理，老师我明白了.

师：同学们，你们认为生2的回答对吗？如何正确解答这道题呢？

（绝大部分同学都表示了赞同，这时一位女生站了起来.）

生 3：利用f（-1）=-f（1）得k=±1，然后再分别检验对其定义域中的所有x是否满足f（-x）=-f（x）.

师：很好，生3的解法体现了特殊到一般的数学思想.还有别的方法吗？

生4：我利用的是奇函数的定义.由于对于定义域中的任一个x值，总有f（-x）=-f（x），通过方程思想对比系数后可得k2=1，从而得到k=±1，我认为这样做比较严谨.

师：是啊，生4的解法也是该题的另一种正确解法，这道题给我们两个启示：（1）函数奇偶性的问题一定要先考虑定义域；（2）奇函数在x=0处有意义才有f（0）=0.从生4的解答中我们还得到一个很有用的技巧：对于等式恒成立问题，可以对比等式两端系数得到方程来解未知数.

（错误往往是正确的先导，是我们最好的老师，错误和挫折可以使我们变得聪明起来——今天的错误就是明天的教训.）

生5：老师，你说这个函数是奇函数，那这个函数应当有对称中心，这个函数的对称中心是什么呢？

（按照原来的设计，学生已经认识了错误的根源，掌握了正确的解法，这个问题可以告一个段落了，况且在这一个没有太多生成空间的问题上过度停留，势必影响我的教学计划，但当我看到生5充满期待的眼神，我心中立刻改变了主意.）

师：你要找对称中心干什么呢？对本题的解答有帮助吗？

生5：老师，找到对称中心，让这个对称中心是原点，不就能确定k了吗？

（生5的回答让我感到很振奋，决定及时抓住这个机遇，引导学生作进一步探究.）

师：思路不错，那我们掌握的知识中与对称中心有关的结论有哪些呢？

生 6：函数f（x）的图象关于点（m，n）成中心对称等价于f（x）+f（2m-x）=2n对一切定义域中的x值恒成立.

师：好，这么说，这应当是一个等式的恒成立问题，刚才我们总结了这类问题的一般解法，那应该是能解决的.

解：显然，k≠0，设其对称中心为（m，n），则对定义域中的每一个x值，均有

f（x）+f（2m-x）=2n成立.接下来如何求解呢？

师：上式对于定义域内的所有x恒成立，怎么处理呢？

生8：通过对比等式两端系数得到等式，求出m，n的值，由上式得

（生5答完后发出得意的笑声，有学生质疑这样做太繁琐.）

师：作为一道填空题，这样来做确实有点繁琐，但是，通过这个问题的解决，我们不仅得出了一类函数的对称中心，而且利用所掌握的知识对未知问题进行了积极的探索.

（正当我欲转入下一个题目时，金子般闪光的声音又响了起来.）

（这帮学生太厉害了，我的兴趣又提了上来.）

师：你们能找到这类函数图象的对称中心吗？

（短暂的紧张运算后，一个同学站了起来.）

生10：函数图象的对称中心为

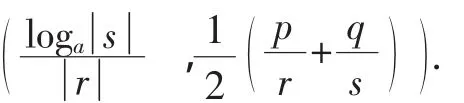
同学们和我都沉醉在探究带给我们的美好享受中，此时时间已过半，我不敢耽搁，准备继续往下讲解例题.

师：至此我们已经探究出这两类一般函数的对称中心.同学们还有什么想法吗？

（不经意的一问，又惹来了“麻烦”.）

生12：老师，对于第二个函数的对称中心也可以这样做：

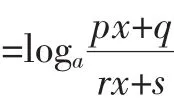
化未知为已知，我和其他同学都被征服了，大家报以热烈的掌声！看到同学们热情如此高涨，我决定放弃原来的教学计划.

师：生12借助原函数与反函数图象间的关系，利用化归的思想求得对称中心，说说看，你是怎么想到求反函数的？

生12：这两类函数的对称中心横、纵坐标交换之后除了相差一个负号，形式基本相同，所以我联想到了反函数，老师，不知道我说的对不对.

（生12显得很兴奋，但又很腼腆.）

师：你真是个机灵鬼，这位同学观察很仔细，我们今后要向他学习.

……

一节课就这样不知不觉地过去了，同学们似乎意犹未尽，研究的热情异常高涨，课后他们根据课堂的研究思路，进行了变题与编题竞赛，收获颇丰.下面是学生的部分成果：

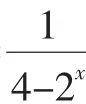
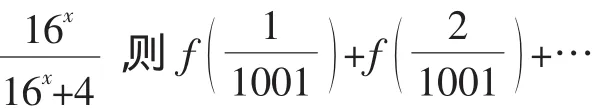
学生的探究活动不仅在课内，还延伸到了课外.而笔者既有惊喜，也有遗憾.

惊喜的是，每个学生都有着探究的热情、探究的欲望和创造的潜能，他们不仅能发现问题，提出问题，而且还能很好地解决问题.

遗憾的是，与长期形成的“规范”的课堂教学相比，心里有一种浪费了时间的感觉.教学未能按计划实施，偏离了预定的教学目标，余下例题的讲解任务，看来要待到下一节课再去补偿了.

二、教学感悟

教了十余年的书，怎样才能使我们的数学课上得更精彩？更高效？笔者陷入了深深的思考之中.

1.捕捉生成问题，形成教学生长点

新课程标准指出：学生的数学学习活动不应只限于接受、记忆、模仿和练习，还应倡导自主探索、动手实践等学习数学的方式.数学探究是新课程的重要理念.如今的数学课堂，学生还是在教师的预设下进行探究，其实还是教师牵着学生的鼻子走，是一种“伪探究”.真正的课堂探究归根结底是以学生是否参与，怎样参与，参与多少来决定的.研究表明，学生对于他们自己提出的即时性问题比较感兴趣.面对这些问题，他们乐于探究、勇于探究，这样的探究才是真正的探究.

教育家苏霍姆林斯基曾说：“教育的技巧并不在于能预见到课堂的所有细节，而在于根据当时的具体情况，巧妙地在学生不知不觉中作出相应的变动.”因此，数学教学中，教师要有捕捉生成问题的意识，对学生暴露出的错误、即兴的提问、独特的见解，教师并不是一味地压制，而是及时地分析、判断并有效地加以利用，使之成为高效课堂的教学生长点.如生5、生12的想法虽在教学预设之外，却彰显了学生思维个性和深邃的洞察力，如果教师不及时捕捉和利用生成问题，就可能错失一次难得的探究机会，它们也会相继被扼杀在思维的摇篮里.反之，教师如果能顺水推舟，让学生充分地发表意见，和学生一起展开思考、探究，那么学生的思考热情和探究欲望会不断高涨，创造火花就会不断迸发，最终导出两类一般函数对称中心的胜利果实.

2.站在学科高度，对待动态生成

课堂教学中，教学活动有时会偏离原来的教学设计，出现“意外”，面对这种“意外”生成，我们不应回避或忙着为自己的下一个环节奔波，我们应当正视和利用这种“生成资源”，尊重学生的需要，从整个高中数学的角度看待这个问题，而不能拘泥于本节课的教学设计，只要是能发展学生思维的，提高学生能力的，锻炼学生意志的，就是值得探究的.如本节课对两类一般函数对称中心的探索，一方面符合高考的需要——考察等式恒成立问题，另一方面也通过探索过程使学生对解决这一类问题的方法留下了深刻的影响，对师生来说是“双赢”.笔者以为，螺旋式的、往复递进的学习过程对学生持久掌握知识会有着明显的作用，很多时候“有效教学”不是针对某节课而言的，而应该把它放在整个高中数学教学体系中，从而客观评价它是否对提高高中教学质量真正“有效”.当然，教师应能判断出学生课堂的生成性问题，是否有价值，并不是学生的任何问题都应在课堂上解决的.否则，个别学生不具共性的问题，在课堂解决，既浪费了其他学生的宝贵时间，也有悖于“有效教学”的要求.

3.开展研究学习，提高探究能力

数学研究性学习是学生数学学习的一个有机组成部分，它强调学习的过程，强调对知识技能的应用，强调学生亲自参与与探索性实践并获得感悟，强调学生的全员参与，即强调学生的主体性.在这一过程中，生生之间、师生之间的相互交流，促使学生不断反思自己的认知，我的理解是什么？我是怎么理解的？我的思路有哪些值得改进的地方？从而自己去发现错误，感受新知，并将其内化为自己的解题经验，最终提高自己在“陌生”情境中的探究能力.如生1见到奇函数就想到f（0）=0的想法，在生2的帮助下立即醒悟过来：那就是奇函数要用f（0）=0必须注意适用范围；生12敏锐的观察能力和别出心裁的求解方法对全班学生都起到了很好的示范——要善于从不同角度解决和探究问题.试想，在这样一种研究和讨论的氛围下，学生一定会在不断地动脑和不断地解决问题的过程中提高分析问题和解决问题的能力，最终促成学生群体创新能力的提高.也只有这样，我们的学生才能在高考中立于不败之地.

1.何智.一堂“偏离”教学目标的高三复习课［J］.中学数学学教学参考（上旬），2009（8）.

2.邵贤虎.意料之外，情理之中［J］.中学数学（上），2010（8）.