关注特征巧变形 有效拓展显功能

☉江苏省新海高级中学 王广余（特级教师）

在数学课堂教学中，选择课本中的典型例题（或习题），恰当实施探究与拓展是新课程背景下富有实效的创新教学，是提高学生思维水平、追求高效课堂的重要途径，是变“教教材”为“用教材”、变“教结论”为“教过程”、创造性地使用教材的根本体现.下面呈现给大家的正是笔者研读教材、悉心备课时，对一道不等式证明题进行变式探究、拓展创新的过程.

题目：普通高中课程标准实验教科书（苏教版）选修2-2第84页练习第3题（直接证明与间接证明练习题）：

一、剖析原题证法，为后继猜想奠基

由于要证的不等式是四个无理数的和式，用综合法证明感觉困难，因而课本采取了分析法证明：

若注意到3-2=6-5的特点，可得到如下简捷证法：

二、关注原题特征，猜想一般结论

题目看似简单，但证明后总觉意犹未尽，从证法2可知隐含条件 3-2=6-5（即 2+6=3+5）及 2＜3＜5＜6 起到了关键作用，由此我们可想到把不等式一般化，猜想其一般结论.

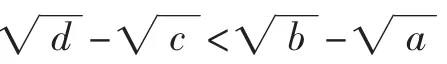
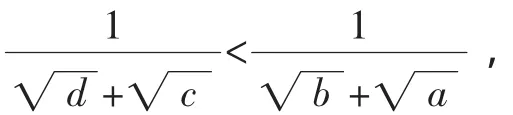
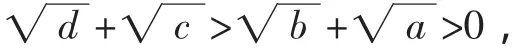
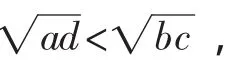
即ad＜bc.

令a+d=b+c=k＞0，

则ad-bc=a（k-a）-b（k-b）=（a-b）［k-（a+b）］，

由a+b＜a+d=k，知k-（a+b）＞0，又a-b＜0，

所以ad＜bc，故原不等式成立.

证法 3：同证法 2，即证ad＜bc，令b-a=d-c=t＞0，得

ad-bc=（b-t）（c+t）-bc=（b-c）t-t2，

因b-c＜0，故ad-bc＜0，即ad＜bc，

故原不等式成立.

证法4：由a+d=b+c平方得a2+2ad+d2=b2+2bc+c2，

（a2+d2）-（b2+c2）=（a+b）（a-b）+（d+c）（d-c）

由题设知a-b=c-d＜0，a+b-d-c=（a-c）+（b-d）＜0，

故（a2+d2）-（b2+c2）=（a-b）（a+b-d-c）＞0，

2（bc-ad）=（a2+d2）-（b2+c2）＞0，即ad＜bc，故原不等式成立.

证法 5：同证法 1，即证ad＜bc，令a+d=b+c=2k，a=kt1，d=k+t1，

b=k-t2，c=k+t2，由a＜b＜c＜d知t1＞t2＞0，

ad=k2-2-，故原不等式成立.

证法 6：同证法 1，即证ad＜bc，由于 0＜a＜b＜c＜d，故只

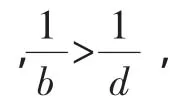
故原不等式成立.

三、拓宽思维途径，深化结论形式

猜想1的六种证法都是从欲证不等式的结构特征出发，通过变更形式，并结合分子有理化、平方作差、引参换元等手段使问题得证，体现了数学转化思想的重要作用.但六种方法有一个共同特点，即它们都得益于条件等式a+d=b+c的有效应用.因此，数学问题的求解与论证中，条件的运用是至关重要的.深入剖析等式a+d=b+c形式，它与等差数列有着内在的联系，由此可得到如下的猜想：

注意到等差数列{an}中，当m+n=k+l时am+an=ak+al成立，故只需证

设等差数列{an}的首项为a1＞0，公差为d≠0.

法 1：aman-akal=［a1+（m-1）d］·［a1+（n-1）d］-［a1+（k-1）d］·［a1+（l-1）d］=［（m+n-2）-（k+l-2）］a1d+［（m-1）（n-1）-（k-1）（l-1）］d2.

因为m+n=k+l，所以由猜想1证法2知mn＜kl，

所以am an-akal=（mn-kl）d2＜0，所以am an＜ak al，

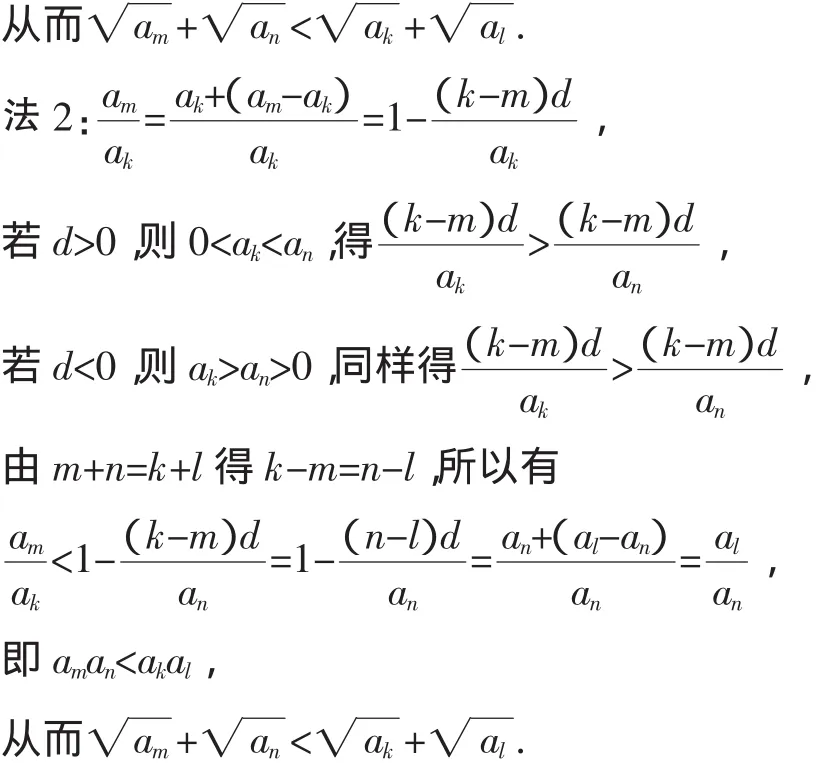
若改等差数列为等比数列，通过类比我们又可得到：

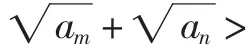
注意到等比数列{an}中，当m+n=k+l时aman=akal成立，故只需证am+an＞ak+al.

设等比数列{an}的首项为a1＞0、公比为q＞0，且q≠1.

由m+n=k+l知n-l=k-m，故有

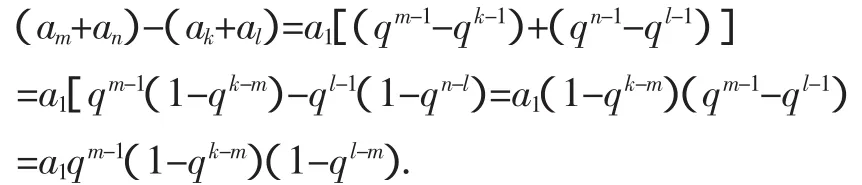
若q＞1，则由k-m＞0，l-m＞0 得qk-m＞1，ql-m＞1，从而（1-qk-m）（1-ql-m）＞0；

若 0＜q＜1，同理可得（1-qk-m）（1-ql-m）＞0，

所以am+an＞ak+al，

若深入思考，类比联想，可进一步探究等差、等比数列的前n项和，得到：

猜想4：设{an}是正项等差数列，公差不为零，其前n项和为Sn.若正整数m，k，l，n满足：m+n=k+l且m＜k＜l＜n，则Sm Sn＜SkSl.

证明：由等差数列的求和公式知要证SmSn＜SkSl，

即证mn（a1+am）（a1+an）＜kl（a1+ak）（a1+al）.

因为m+n=k+l且m＜k＜l＜n，

所以由猜想1的证法2可知mn＜kl，只需证

（a1+am）（a1+an）＜（a1+ak）（a1+al）.

又因为am+an=ak+al且aman＜akal，

所以（a1+am）（a1+an）-（a1+ak）（a1+al）=am an-akal＜0，

由此可知SmSn＜SkSl成立.

猜想5：设{an}是正项等比数列，公比不为1，其前n项和为Sn.若正整数m，k，l，n满足：m+n=k+l且m＜k＜l＜n，则Sm Sn＜SkSl.

证明：由等比数列的求和公式得

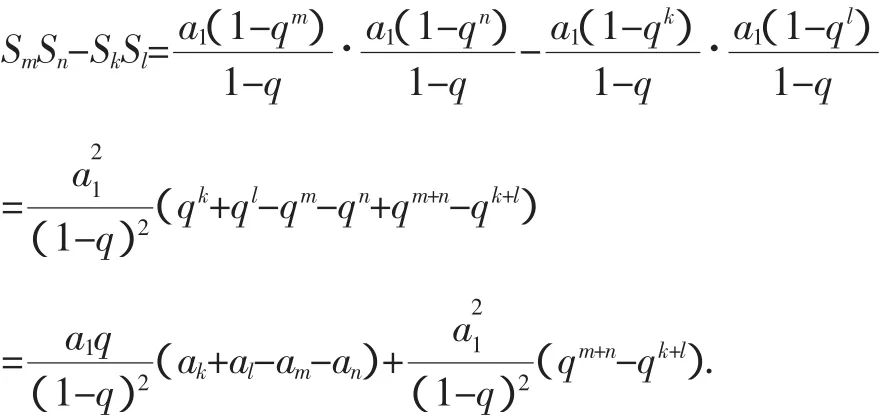
因为m+n=k+l且m＜k＜l＜n，

所以由猜想 3 知am+an＞ak+al且qm+n=qk+l，

从而有SmSn-SkSl＜0，即SmSn＜SkSl.

现行高中数学教材在“以人为本”这一新课程核心理念的引领下，为学生创设了多元化、多层次、有梯度、有意义的选择资源，也为教者增添了扩充拓展、变式出彩的教学空间，因此教材中具有丰富的可供变式探究、拓展深化的素材，在数学课堂教学中，我们应充分运用这些素材，有针对性地引导学生开展自主探索，通过一题多解达到追求简洁结果、优化解法的目的，通过一题多变达到举一反三、触类旁通、促进良好迁移之功效.