问渠哪得清如许 为有源头活水来——例析“活用”、“巧用”基本不等式解题之“定值”条件的获取

☉重庆市梁平实验中学 蒋明建

用基本不等式求函数的最值以及证明不等式是高中数学非常重要的内容，也是高考热点，在历年各地的高考试题中频频出现直接或中间过程运用基本不等式求解的题目，可谓常考不衰、常考常新.玄机何在？我们知道，应用基本不等式必须同时具备“一正（各项值为正）、二定（各项的和或积为定值）、三相等（取“等号”的条件）”这三个条件，缺一不可.在具体的题目中“正数”条件往往容易从题设中获得，“相等”条件也容易验证确定，而“定值”条件涉及各种数学式子的“和”、“积”，既是式子的表现形式又是运算形式，可静可动灵活多变，不拘一格，因此，“定值”条件往往以某种形式隐蔽在所给数学式子中（通常是命题者设计的一个难点），要获得此条件需要对所给的解析式进行适当的变形，具有很强的灵活性和技巧性.可见，有效实现基本不等式“和定”“积定”条件，就找到了“活用”、“巧用”基本不等式解题的源头.怎样才能有效获得“和定”“积定”这一重要条件呢？通常统称为“配凑”、“构造”，笔者在此通过对一些典型题目的解析，将本人在教学中应用基本不等式解题时获取“定值”的一些常用、细化方法作一个归纳、梳理，望能对读者有一定借鉴作用.

一、加项、减项变形

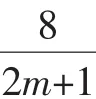
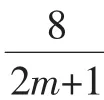
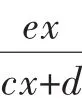
二、乘、除变形

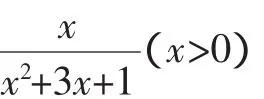
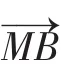
（1）求C的方程；

（2）点P为C上的动点，l为C在点P处的切线，求O点到l的距离.

评注：这两个问题都比较简单，却是很具有代表性的常见问题，属于一次比二次或二次比一次的分式函数求最值问题，通常都可以采用乘除变形，使题目隐藏的“定值”条件显现出来，从而在分母或分子中能够用均值不等式，使问题变得易于求解.

三、平方、开方变形

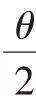
四、代换变形

1.常值代换

例5 （2010年湖北武汉调研）过定点P（2，1）的直线l交x轴正半轴于点A，交y轴正半轴于点B，O为坐标原点，则△OAB周长的最小值为（ ）.

A.8 B.10

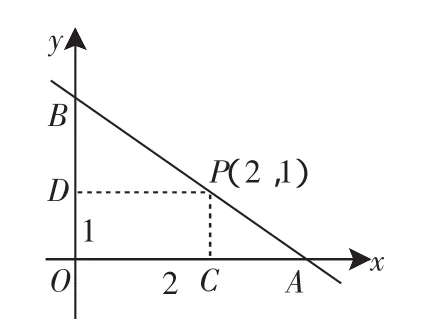
图1

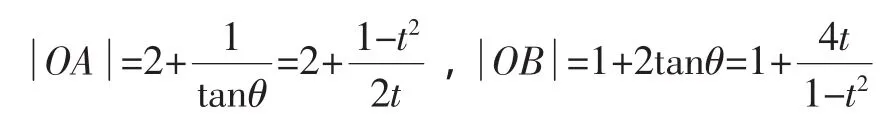
评注：这是一道难题，想到用分母之和“t+（1-t）=1”进行常值“1”代换，构成“积定”条件，从而用基本不等式求解，好比用“四两砣拨动了千斤鼎”，化难为易，化繁为简，大大简化了解题过程.“1”代换解决有些数学问题很巧妙，望注意适时应用，能用时切不可弃之不用.

2.变量代换

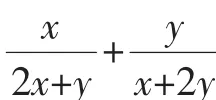
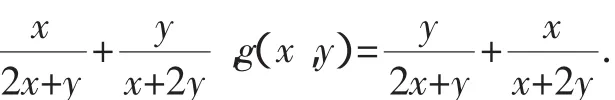
3.整体代换

例 7 已知x、y、z均为正数，xyz（x+y+z）=1，求（x+y）（y+z）的最小值.

评注：能观察出用这种整体代换变形，实现均值不等式的“积定”条件，十分巧妙.代换法是数学中应用最广泛的一种方法，在解题中若能熟练灵活地应用，将大大简化解题过程，收到事半功倍的效果.

五、代入（消元）变形

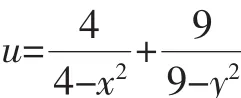
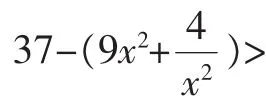
六、分解与组合变形

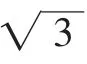
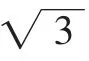
评注：这类题考查了较强变形式子的能力，打破了题目中式子原有结构，或分解或重新优化组合，构成基本不等式“和定”、“积定”特征形式，然后利用基本不等式，体现了“不破不立”的思想，在高考题中频频出现，如2010年重庆高考题（理 7）“已知x＞0，y＞0，x+2y+2xy=8，则x+2y的最小值”便属于这一类题，值得重视.

“分久必合，合久必分”，分解与组合是相对的，它们相互联系又互相转化，这是客观事物发展中的必然规律，把这一规律运用到数学解题中就是分解与组合的思想，望认真体会切实掌握.

七、重复使用基本不等式

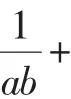
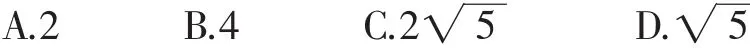
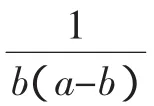
评注：求解最值问题时，有时需要同时或者连续多次使用基本不等式，这时一定要注意使用条件必须一致，即每次取得“=”的条件要一致，否则求出的结果是错误的.重复使用基本不等式求解的高考题出现的频率相当高（见 2011 年湖南，2009、2007、2005 年重庆，2008 年江苏等地的高考题），望能足够重视.

八、待定系数法变形

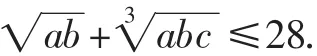
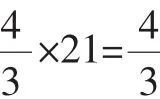
评注：分析题目结构，根据题目中的数“21”与“28”的关系，将问题合理转化是解决本问题的切入点，运用待定系数法确定需要“配凑”的系数是解决本问题的一把利器.

以上各题目从所给出的式子形式来看，都不能直接应用基本不等式求解（有的可以用其他方法求解），其原因在于不完全具备基本不等式的“正”、“定”、“等”三个条件，特别是“和定”、“积定”的条件不明显，只有通过相应的变形转化后才可实现.由此可见，“定值”条件决定着基本不等式应用的可行性，是解题成功的关键（在取得最值时，还必须要各项相等，这是检验“定值”转换是否正确的一种方法）.本文中共举例介绍了常用的八种构造“定值”的变形方法，值得注意的是，在具体的解题过程中，每一个题并不是只用其中的一种方法，往往是几种方法的综合运用.也正因为“定值”条件得以实现的变形方法如此灵活多样、丰富多彩，才使得基本不等式如此地充满了生机与活力，让人感受到数学的无穷奥妙和神奇；也正因为基本不等式的“活用”、“巧用”能给我们的思维提供广阔的发展空间，才会让人们学习起来充满了乐趣和美的享受，才会使运用基本不等式求解的高考考题层出不穷、常考不衰、常考常新.“问渠哪得清如许，为有源头活水来”，“活用”、“巧用”基本不等式解题的源头正在于此.

1.史美初.应用平均值不等式，在“活”与“巧”上下功夫［J］.中学数学教学参考（上旬），2005（1-2）.

2.安振平.妙用二元均值不等式证明不等式［J］.中学数学教学参考（上旬），2008（9）.

3.蒋明建.善用“1”巧解数学题［J］.高中数学教与学，2010（4）.