多元问题 “减元”处理——一道多元函数最值问题的多解及反思

☉湖南省衡阳县职业中专 龙向东

学习数学的最终目的之一就是能够用所学的数学知识解决问题.重视从不同的角度认识题目，并能够充分揭示题目中蕴涵的信息，并从中获得不同的解法，这无疑对培养学生思维的广度、深度与灵活性，培养学生的创新精神，训练发散思维，进而对学生综合解题能力的提升起着重要的作用.

一、问题提出

已知x，y，z∈R，且x+y+z=1，x2+y2+z2=3，则xyz的最大值为______.

本题（源自2011年全国高中数学联赛B，T9，原题：已知实数x，y，z满足：x≥y≥z，x+y+z=1，x2+y2+z2=3，求实数x的取值范围）条件简洁明了，结构对称优美，题意清晰而又内涵丰富.

二、解法探究

则①2-②，得2xy=（1-z）2-3+z2=2z2-2z-2，（*）

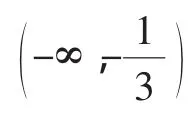
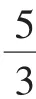
当且仅当x=y时取到等号.

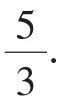
评注：目标式中有三个元，故从化归转化的角度看，减元转化为单元函数的值域问题是方向，减元的技巧则是通过x+y与x2+y2的结构差异联想到可用z来表示xy，另一个问题是如何准确界定z的范围？解法1是通过（*）和②两式结构特征联想到它们之间隐含的均值不等式，从而得到关于z的另一个不等式.

解法2：由题意，将z=1-（x+y）代入x2+y2+z2=3，得

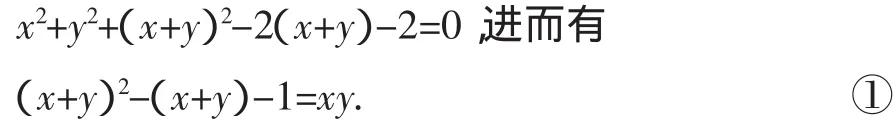
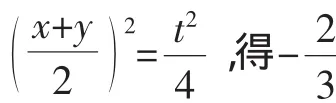
评注：本解法与解法1异曲同工，由于观察的角度不同，所采取的换元思路是不一样的，本法是用x，y表示z，再根据x+y与x2+y2的结构特征，用x+y整体表示xyz，而对于新元的范围界定仍是通过不等式获得，需要指明的是此类范围限定中，往往需结合利用到两个条件式的不等式才能获得最终的范围.

事实上，还有学生是这样减元的：1=（x+y+z）2=x2+y2+z2+2（xy+yz+xz）=3+2xy+z（x+y），从而xy=-1-z（1-z）=z2-z-1，下同解法1.尽管过程未必简洁，但却透露重要的一点：至少学生发现了可以利用所学知识之间的结构特征联系寻求解题的突破口，比如学生因为发现（x+y+z）2的展开式中含有xy，所以以此为开端逐步达到目的.G.波利亚在《怎样解题》一书中这样表述：“你应该考虑它，如果它看上去很有利，你应该考虑得更久一些；如果它看上去很可靠，你就应该弄清楚它能引导你到多远，由于这个有用的念头，整个情况已经发生了变化并从不同的方面重新考虑新的情况，寻找你与过去所获知识之间的联系.”或许有这方面的意思吧，教学中可以从题目的特点、条件结构等方面去指导学生解题.而对于解法1中函数f（z）=xyz=z3-z2-z中自变量z的范围界定，还可以利用条件的结构特征求解.

解法3：由解法1可得

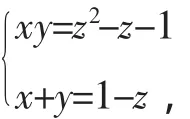
评注：通过x+y，xy与二次函数中根与系数关系式的结构相似性获得构造的灵感，找到了突破口，可谓巧妙.类似地还可以采用解法4.

评注：此法从条件式本身的方程结构上联想挖掘出了几何图形：直线与圆，结合题意转化为相关解析几何知识求解，巧妙的得到了范围，其独特的视角让人叫好.

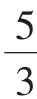
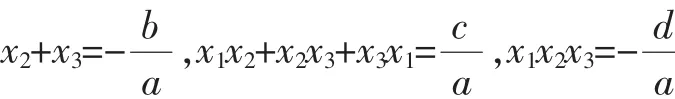
当然，就本题而言，从条件的结构特征角度观察，是否还可以转化为空间直角坐标系下平面x+y+z=1与球面x2+y2+z2=3有关的问题来求解，其中xyz是否可以理解为立方体的体积？是否可以通过选修教材中的球坐标方程来求解？是否还有其他的解法？这些都值得进一步研究.

三、反思

上述解法，体现了化归思想的运用.化归转化思想是指运用某种手段或方法把待解决的较为生疏或较为复杂的问题转化归结为熟悉的规范性问题来解决的思想方法.化归转化思想是考生解决难题时常用的手段，也是高中数学思想方法的重要内容.在解题实践中，大部分试题的条件与目标的联系不明显，能否根据问题的特点、条件与结论的结构和解题中出现的具体情况“随机应变”，调整思路、转换策略，是我们能否顺利解题的一个关键因素，也是思维灵活性的一个重要体现，强化解题过程中的应变能力，有利于提高解决数学问题的思维能力.数学的符号化、形式化特征，为化归思想的使用提供了便利条件，因为数学的符号语言具有演算性、形式化、符号化的特点，较易找到化归的目标和方向.所以教学中：一方面，应该重视在化归转化思想指导下启发引导学生从题目条件、结论的结构特征上去寻求解法，高中解题活动中经常能用到这样的结构转化，但如何能做到这样的联想呢？“其一能识别结构，特别是特征明显的结构；其二能建立知识的框架体系，在这个体系下熟悉知识间的联系、转化、迁移、发展等，建立函数、不等式、方程的联系，建立向量、几何、代数、三角的联系，建立求函数最值的模型结构与匹配的方法间的联系等”；另一方面，应该鼓励学生多角度、全方位地深入探索，“一题多解”作为训练学生的发散性思维、培养和提高学生思维能力是一种很好的方法.另外还应注重解题后的反思归纳并注意突出通性通法，主要从解题结果、解题过程（对已有解法的回顾，包括计算是否正确，推理是否合乎逻辑，思维是否缜密等；探讨解法的多样性）、解题思想方法、习题特点等方面引导学生归纳反思，反思是学生提高解题能力的重要手段，本题解法较多，主要有基本不等式法和函数转化法，这些方法将函数、三角、不等式乃至几何的相关知识有机地联系起来，这对于完善数学认知结构、提高思维的灵活性以及解题能力有着重要的意义.进一步地可从问题的结构特点、解题的思路和途径等多种角度引导学生去观察、感悟、联想、归纳，要多问：解法结果有无问题？过程是否完整？哪种解法更简单？哪种解法更常规，更巧妙，更典型？各解法的特点如何？阻碍解题的难点在哪里？能将上述解法分类么？解法中还涉及哪些知识？是否可以体会到解法中隐含的数学思想？

1.边欣.一道2011年全国高中数学联赛试题的简解［J］.数学通讯，2012（2）.

2.沈良.略谈数学结构观下的解题与教学［J］.数学通讯，2012（12）.