彰显解题功能 提升解题境界

●

(蒋王中学 江苏扬州 225126)

彰显解题功能提升解题境界

●严高明曹松青

(蒋王中学 江苏扬州 225126)

我们知道，数学解题主要有这样几种功能：教育功能、优化功能、拓展功能等,因此解题教学的目标绝不能仅仅定位于就题论题，简单地帮助学生获得答案，应当从达成并完善上述几种功能的角度去着意挖掘问题的剩余价值，提升解题境界.下面以一道小题为例来谈谈笔者的一些做法，供参考.

图1

题目如图1,点P(3,4)为圆x2+y2=25上的一点，点E,F为y轴上的2个点，△PEF是以P为顶点的等腰三角形，直线PE,PF交圆于点D,C，直线CD交y轴于点A,则直线CD的斜率为______.

1 彰显教育功能

本题最自然的思路是：设出直线PD的方程，与圆的方程联立，求出点D的坐标.同理求出点C的坐标，利用两点间直线斜率公式，求出直线CD的斜率.思路自然、运算繁琐，以至于不少学生一遇见这类问题，就产生恐惧心理，敢想而不敢为.从学生的长远利益着想，回避显然只是权宜之计，只会滋长学生的畏难情绪，影响其解题心理机制.这种负面影响甚至殃及到学生的将来，使得其在将来的学习和工作中表现出拈轻怕重、怕苦畏难的态度和作风.从这个角度去考虑，笔者认为还是要坚持让学生沿着这个最自然的思路将计算进行到底.这样就充分彰显了问题的教育功能，从而培养了学生知难而进的探索精神，让学生成为解题勇者.

2 彰显优化功能

上述通解虽然具有强大的教育功能，但是阻挡不了学生对简洁美的追求.事实上，数学时刻以它的简洁美召唤着探索者.在解题教学过程中，我们必须努力去探索、去寻求优美解，彰显解题的优化功能，让学生在优化中成为解题智者.

图2

优化1注意到本题是填空题，答案显然与点C,D位置无关，故可将其中一点特殊化(放到坐标轴上去).解法如下：

如图2，取C(-5,0)，则

代入圆x2+y2=25,得

5x2-22x+21=0.

于是

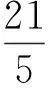
从而

图3

优化2考虑到特殊值法有投机取巧之嫌，显然不具有强大的说服力，我们更欣赏的是凭借数学自身的力量去解决问题.事实上，在解决解析几何问题时，若能挖掘问题的几何意义，借力于平面几何中的结论，则将大大减少计算量.若从平面几何的角度审视该问题，则不难发现如下解法：

∠ANP=∠MPC+∠ACP=∠DPM+∠ACP=∠MCP=π-∠MHP,

所以

即

优化3在上述优化2的基础上，继续挖掘几何意义，还会得到如下更简洁的解法：

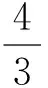
通过逐级优化，问题豁然开朗，且学生解决问题的视角也被大大拓宽，解题境界也得以大大提升.

3 彰显拓展功能

虽然问题已得到较完美的解决，但考虑到此问题的发展功能，还可引领学生将问题进一步拓展：

如果将上述问题一般化，拓展为如下问题：

由于字母的增加，计算量就会陡增，这时会给教学带来新的课题，即如何降低计算量?当然可采用上述优化3的方法加以证明，但考虑到若问题背景不是圆，则难以从几何的角度来解决.从发展功能的角度来看，采用代数解法虽然繁琐一些，但更具有长远意义.因此，笔者还是引导学生从宏观上把握问题的整体性，得到如下代数证法：

证明设CD：y=kx+t，即

圆x2+y2=r2可化为

[(x-a)+a]2+[(y-b)+b]2=r2,

即 (x-a)2+(y-b)2+2a(x-a)+2b(y-b)=0.

(2)

由式(1)和式(2)，得

即

两边同除以(x-a)2,得

从而

因为kPC+kPD=0，所以

图4

在拓展1的基础上，顺势将本题圆的背景设置为椭圆背景，得到如下拓展：

显然学生只需对拓展1的解法作一简单模仿，便可解决拓展2.但许多学生还是不乐意去实施，因为计算量太大了，在他们的内心深处有一个“梦想”：问题背景是圆，该有多好呀！考虑到椭圆是由圆压缩而成，因此笔者引导学生实施一个小小的压缩变换，将椭圆变为圆，“圆”了他们的梦.具体证法如下：

当然，本题中还可以圆的背景拓展为双曲线、抛物线等，这里不再赘述.

以上探究过程，就“恍如由傲来峰西面攀登泰山的景象：初看傲来峰峭壁千仞，以为上与天通；及至翻到傲来峰顶，才见扇子崖更在傲来峰上；及至翻到扇子崖，又见南天门更在扇子崖上：愈翻愈险，愈险愈奇”.解题教学不就如同登泰山吗？只要我们坚持去彰显解题功能，久而久之，学生的解题境界就必定会得到提升，也必定会成为解题的勇者、智者、思者……

[1] 严高明，曹松青.警惕！学生的计算自信在丧失[J].中学数学教学，2013(4)：11-13.