对一个二次曲线结论的深度探究

●

(杭州学军中学 浙江杭州 310012)

对一个二次曲线结论的深度探究

●郑日锋

(杭州学军中学 浙江杭州 310012)

文献[1]用了较大的篇幅，最后得出了如下的统一结论：

过二次曲线Ax2+Cy2+Dx+Ey+F=0(A2+C2≠0)上一点P(x0,y0)的2条直线与曲线交于点A,B，满足kPA·kPB=t(t≠0).若此二次曲线方程经过x′=x+x0,y′=y+y0换元后的方程为

A′x′2+C′y′2+D′x′+E′y′+F′=0(A′2+C′2≠0),

1 完善

此结论可以完善为如下定理1.

定理1过非退化的二次曲线Γ:Ax2+Bxy+Cy2+Dx+Ey+F=0上一点P(x0,y0)的2条直线与Γ交于点M,N，满足kPM·kPN=t(t≠0).

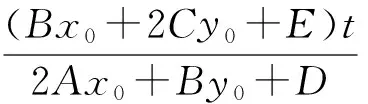
证明设直线MN的方程为

因为点P在二次曲线Γ上，所以二次曲线Γ的方程可以化为

A(x-x0)2+B(x-x0)(y-y0)+C(y-y0)2+(2Ax0+By0+D)(x-x0)+(Bx0+2Cy0+E)(y-y0)=0,

(2)

由式(1)，式(2)得

A(x-x0)2+B(x-x0)(y-y0)+C(y-y0)2+[(2Ax0+By0+D)(x-x0)+(Bx0+2Cy0+E)(y-y0)][m(x-x0)+n(y-y0)]=0,

即

[A+m(2Ax0+By0+D)]=0.

(3)

设M(x1,y1)，N(x2,y2),由kPM·kPN=t得

[C+n(Bx0+2Cy0+E)]s2+[B+n(2Ax0+By0+D)+m(Bx0+2Cy0+E)]s+[A+m(2Ax0+By0+D)]=0

的2个实根，由韦达定理得

由式(4)，式(5)得

即

(2Ax0+By0+D)m=Ct-A+t(Bx0+2Cy0+E)n.

(1)若Ct-A=0，则

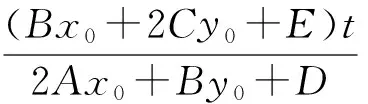
②当2Ax0+By0+D=0时，Bx0+2Cy0+E≠0(否则，若Bx0+2Cy0+E=0，二次曲线的方程变为A(x-x0)2+B(x-x0)(y-y0)+C(y-y0)2=0,此时二次曲线Γ为退化的二次曲线)．因此n=0,直线MN的斜率不存在．

(2)若Ct-A≠0，则

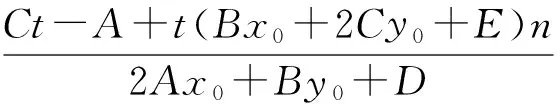
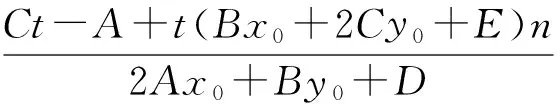
即(Ct-A)(x-x0)-(2Ax0+By0+D)+[t(Bx0+2Cy0+E)(x-x0)+(2Ax0+By0+D)(y-y0)]n=0.

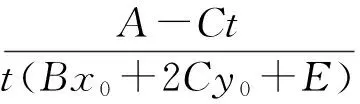
因此，直线MN过定点

以上证明过程通过巧设直线MN的方程，并把二次曲线方程化为关于x-x0,y-y0的方程(缺常数项)，于是构造以kPM,kPN为实根的一元二次方程，进一步利用韦达定理，得到关于m,n的关系式，从而得到结论.整个过程自然简洁，对于具体的问题也很容易操作．

2 联想

至此，我们自然会产生联想：如果改为kPM+kPN=t，结论如何？

由定理1的证明过程很容易得到如下定理2.

定理2过非退化的二次曲线Γ:Ax2+Bxy+Cy2+Dx+Ey+F=0上一点P(x0,y0)的2条直线与Γ交于点M,N，满足kPM+kPN=t(t为常数)．

[1] 徐存旭．大胆猜想 小心求证 逐步推广[J]．数学通报，2012(5)：40-43.