探寻解题模块　实施有效教学

黄　雯

(江苏省常州市第二中学，213003)



○教学研究○

探寻解题模块实施有效教学

黄雯

(江苏省常州市第二中学，213003)

解题模块是一种重要的认知结构,在高中数学解题教学中发挥着不可估量的作用．解题模块帮助学生在自己头脑里形成对某类数学问题的解题结构,将看似杂乱无章的解答变得有章可循,有法可依,从而最大限度地降低学生学习高中数学的难度．本文通过几类具体的数学题型,来说明解题模块在教学中的实践应用．

某次考试过后,一位老师在班里狠狠地批评了一些学生,原因是一道他已经讲过好多遍的题目还是有不少学生出了错．对于在一线勤恳耕耘的数学老师们可能都会碰到这样的情况:为什么反复强调、反复讲解的题型学生还是会出错?似乎教师的讲与学生的理解完全不搭界,你讲你的,他错他的．如果能够找到解决这一问题的行之有效的对策,相信对于高中数学的减负增效有着最直接的效果．

一、解题模块举例

张景中院士在谈到解题的时候说过一段精彩的话:“练武功的上乘境界是‘无招胜有招’．但武功仍要从一招一式入门．解题也是如此…这种‘无招胜有招’的境界,就是‘大巧’吧!但是小巧固不足取,大巧也确实太难,对于大多数学子,还要重视有章可循的招式…大巧法无定法,小巧一题一法．中巧呢,则希望用一个方法解出一类题目．也就是说,把数学问题分门别类,一类一类地寻求可以机械执行的方法,即算法．”

在怎样教授学生解题这个问题上,笔者认为要善于探寻解题模块．换言之,也就是帮助学生在自己头脑里形成对某类数学问题的解题结构．其实有很多数学题我们都可以想办法把隐性的解题经验显性化、算法化,将看似杂乱无章的解答变得有规律可循,有方法可依,从而最大限度地降低学生学习高中数学的难度．下面将通过几类具体的数学题型,来说明解题模块在教学中的应用．

题型1不等式恒成立问题

例1对于∀x∈R,不等式x2-x+2-m≥0恒成立,求实数m的取值范围.

解设f(x)=x2-x+2-m.

因为 ∀x∈R,f(x)≥0，所以Δ≤0 ，

即1-4(2-m)≤0，

变式1对于∀m∈[-2,2],不等式x2-x+2-m≥0恒成立,求实数x的取值范围.

分析在变式1中,m是变量,x是参数．将不等式变形为m-x2+x-2≤0,设f(m)=m-x2+x-2,这是关于m的一次函数,问题转化为使得f(m)≤0恒成立的问题．

解设f(m)=m-x2+x-2,m∈[-2,2],它是关于m的一次函数,要使f(m)≤0,只需两端点的函数值小于0,即

解得x∈(-∞,0]∪[1,+∞).

点评(1)在处理不等式恒成立问题时,首先需要判断哪个字母表示变量,哪个字母表示参数;

(2)上述两个例子的解法利用了“函数的保号性”．

如果f(x)是一次函数,设x∈[m,n],那么它的符号取决于两个端点函数值的符号,即

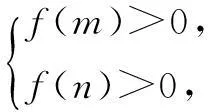
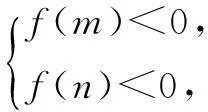
如果f(x)是二次函数,x∈R,那么它的符号取决于开口方向和判别式,即

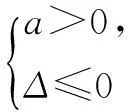
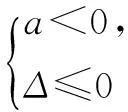
变式2对于∀x∈[1,2],不等式x2-mx+5≥0恒成立,求m的取值范围.

分析x是变量,m是参数．本题是二次不等式,变量x在区间[1,2]上变化,这与例1中x∈R不同．

解法1设f(x)=x2-mx+5,当x∈[1,2]时,f(x)≥0恒成立,等价于f(x)在[1,2]上的最小值大于等于零.

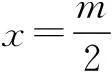
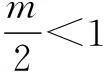
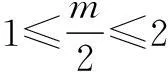
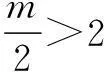
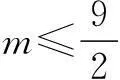
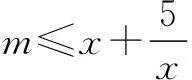
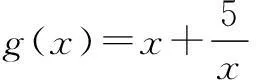
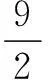
点评变式2的解法2是“参变分离法”,这个方法也经常用在不等式恒成立问题中．在参变量易分离的情况下,通常将不等式转化为f(k)≤g(x),x∈[m,n]的形式,左边只含有参数k,右边只含有变量x,那么原不等式恒成立问题就等价于f(k)小于等于g(x)在x∈[m,n]上的最小值M,解f(k)≤M,便得到相应的结论．

小结不等式恒成立问题的解题策略,大致归结为以下两个步骤.

(1)判断：判断问题中出现的字母哪个是变量,哪个是参数;

(2)方法：常用的方法有函数的保号性法、参变分离法．

题型2等差数列前n项和的最值

例2已知等差数列{an}的通项公式为an=3n-22,求当n为何值时其前n项和Sn取到最值.

解法1因为a1=-19<0,d>0,所以Sn有最小值.

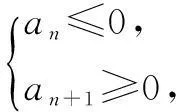
因为n∈N*所以n=7时,Sn有最小值.

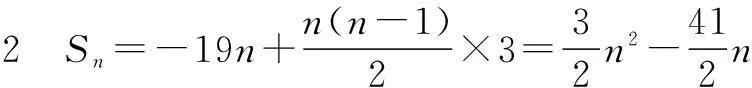
因为n∈N*，所以n=7时,Sn有最小值.

点评对于首项a1,公差d都确定的等差数列,我们可以从两个角度考虑.

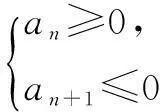
变式1已知{an}是等差数列,a1=13,前n项和为Sn,且S3=S11,求n取何值时,Sn有最大值.

解法1由S3=S11得d=-2.

所以an=13+(n-1)×(-2)

=-2n+15.

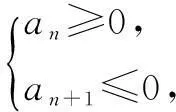
因为n∈N*， 所以n=7时,Sn有最大值49.

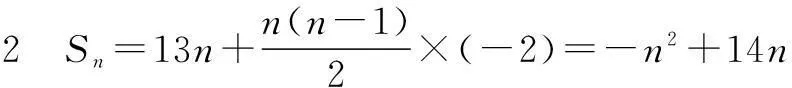
因此n=7时,Sn有最大值49.

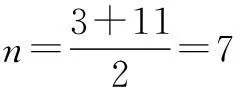
点评变式1的解法3可以看作是第三种方法：图象法．在已知S3=S11的情况下,利用Sn二次函数的图象对称性,直接求出对称轴解决问题．

小结求等差数列前n项和Sn最值的三种方法:

(1)从项出发．先判断是哪一类情形(a1<0,d>0或a1>0,d<0),再根据不等式组找到an符号的转折处;

(2)从和出发．把Sn看成是n的二次函数,通过求对称轴,确定函数最值在哪里取得;

(3)图象法．利用二次函数图象的对称性,直接求对称轴解决问题．

二、探求解题模块的注意点

首先,不是所有的数学题都可以归结到某一类型中去的．比如,证明题、开放题,通常它们都没有具体的操作步骤可以套用．

其次,教师在要求学生识记解题模块之前一定要讲清问题的来龙去脉,揭示蕴含在其中的数学思想方法,让学生在理解透彻的基础上加以记忆.否则,光是死记硬背的话很容易出现错误．

再者,一个好的解题模块中还应该包含有具体的实例,并且可以让学生在理解的基础上进行适当地记忆．当然例子要有典型性,这样学生解题时遇到类似的地方,就可以联想到解题模块中的例题,将例题中的方法迁移到解题中．

最后,笔者提出解题模块并不排斥其他创新的方法.相反地,教师在介绍“通法”的基础上适时补充一些“巧法”,更有利于学生发散性思维的培养．

达尔文曾经说过:“最有价值的知识是关于方法的知识．”教师在和学生通过习题不断地总结解题经验中，可以进一步地完善各种题型的解题模块,将其应用到解决新问题中去,促进知识的迁移．同时,解题模块的引入还培养了学生良好的反思习惯,尤其是当面对自己的错题时,学生会主动思考这属于哪一类题型,应该用怎样的方法来解决,甚至能主动归纳错题类型,将其纳入到已有的解题模块中或者创建一类新的解题模块．