方法本天成　“构造”巧得之
——浅谈高中数学解题中的构造法

王　华

(江苏省吴江中学，215200)



○解题研究○

方法本天成“构造”巧得之
——浅谈高中数学解题中的构造法

王华

(江苏省吴江中学，215200)

数学构造法是指在解决问题时,构造与原问题有关的数学模型,通过研究这些数学模型,找到解决问题的方法．它的基本原理就是借用一类我们熟知的问题性质,去探求未知问题的性质．

一、六种常见构造方法

1. 图形构造法

数学中的很多数量关系都隐藏着形的信息,利用图形中的相应信息可以很形象地反映出问题中的本质关系．图形构造法能为数与形构建一座桥梁,使问题更明朗化．

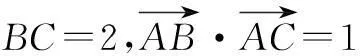
解法1(一般方法)依题意，有

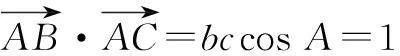
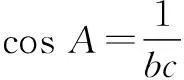
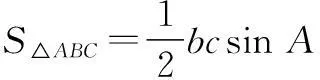
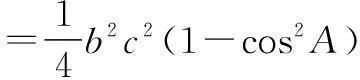
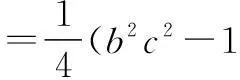
由余弦定理，得4=b2+c2-2,即

b2+c2=6，

∴6=b2+c2≥2bc,即bc≤3，

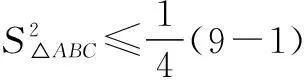
解法2(构造法)根据三角形面积公式,∆ABC的面积底边是定值,只有高是变化的量,且和点A的位置有关,因此可以研究点A的特点．

如图1,构建平面直角坐标系,使得B(-1,0),C(1,0).不妨令A(x,y)，则

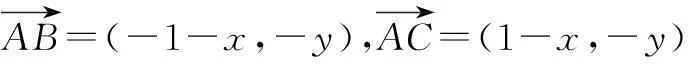
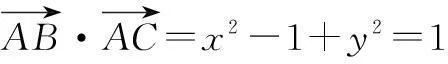
即x2+y2=2，

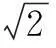
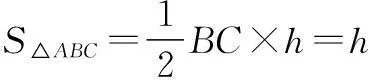
其中h为点A到BC得距离.

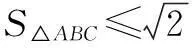
2. 函数构造法

构造函数法是数学解题中比较常见的方法之一.巧妙构造一个函数,利用函数的性质去解决问题,可以达到解题目的．

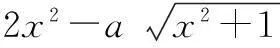
分析本题如果直接去研究不等式左边的条件,会比较难处理,因此本题首先应该对不等式进行等价处理．

解法1由题意,题中的不等式恒成立等价于不等式

对任意x∈R恒成立.

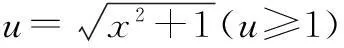
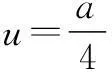
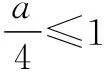
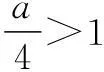
∴a<3.

解法2由题意，不等式等价于

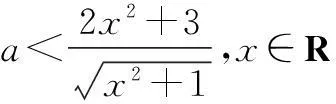
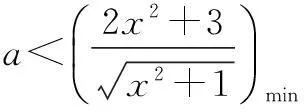
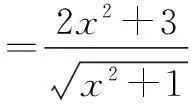
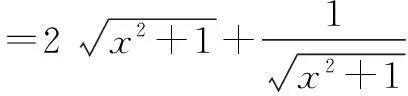
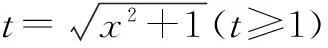
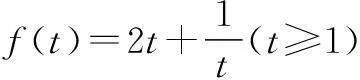
∵f(t)在[1,+∞)上为单调增函数，

∴f(t)≥f(1)=3,即f(t)min=3,

∴a<3.

这两个方法虽然过程不同,但都是构造某一个函数,通过研究函数的性质,使问题得以解决．

3. 向量构造法

在高中数学中,向量知识往往是作为解题的重要工具,向量的运算有坐标运算,也有图形(三角形或平行四边形)运算,是数形结合的重要工具．因此利用向量解决数学问题可以更简便快捷．

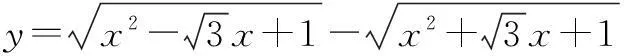
解将函数解析式变形，得

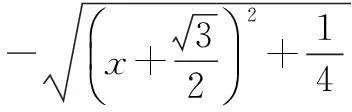
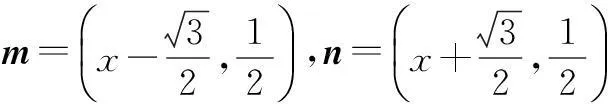
注意到m,n为不共线向量,则有

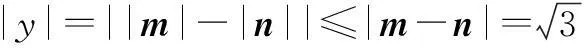
4. 方程构造法

解方程思想是数学解题中的重要思想方法,如果在解题过程中能找到已知与未知之间的等式关系且具有方程的某些特性,就可以考虑去构造一个方程,使数学问题得以解决．

例4已知a,b,c满足a+b+c=9,ab+bc+ca=24,试求b的取值范围．

解由题意可得c=9-a-b，代人ab+bc+ca=24，得

a(9-a-b)+(9-a-b)b+ab=24，

整理得a2+(b-9)a+b2-9b+24=0.

此方程可看作是关于a的二次方程,则相当于此二次方程有实数解，

因此有 (b-9)2-4(b2-9b+24)≥0，

解此二次不等式，得b∈[1,5].

5. 基本不等式构造法

基本不等式是高中数学中的重要知识之一,在高考中的要求比较高,在应用时往往和其它知识相结合,特别是和函数问题,取值范围问题联系比较密切．

分析此类问题,我们一般采用分离常数的方法,再利用基本不等式求解．

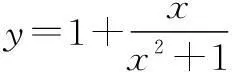
当x=0时,y=1；

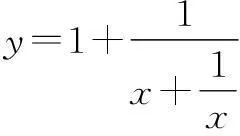
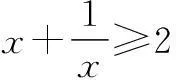
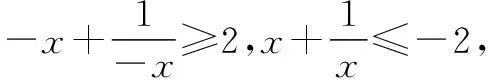
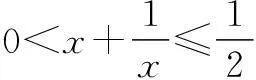
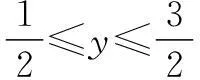
6. 等价命题构造法

当我们在研究一些数学命题时,发现直接论证比较困难时,我们可以考虑去构造命题的否命题,再通过研究相应的等价命题来解决问题．

例6已知命题:“∃x∈[1,2],使x2+2x+a≥0”为假命题,试求a的取值范围．

解由题意,此命题的否定形式为“∀x∈[1,2],使x2+2x+a<0”为真命题.

这等价于x2+2x+a<0对∀x∈[1,2]恒成立，

即等价于a<-(x2+2x)对∀x∈[1,2]恒成立.

不妨令f(x)=-(x2+2x)=-(x+1)2+1,∴f(x)min=f(1)=-3.

∴a<3.

二、教学感悟

1. 注重对学生阅读能力的培养

构造法解题需要学生对数学问题有一些创新的的想法,这离不开学生较强的“读题”能力,即数学阅读的能力．数学课程标准强调:注重学生各种能力的培养,其中包括数学阅读能力、数学应用能力和数学探究能力．在平时的教学中,有意识地去指导学生进行数学阅读,教会学生一些常见的数学阅读方法,通过阅读能力的提高来达到“读题”能力的提高,从而从“机械读题”到“意义读题”的提升.这样的话,构造法解题需要的隐蔽条件就会在学生较高的阅读能力下捕捉到．

2. 培养学生将所学知识点网络化的能力

构造法解题对学生的知识掌握要求比较高,需要建立知识之间的联系才能解决相关的数学问题.因此，在进行知识点教学和复习时,要关注知识点之间的联系,不仅要体现在它们之间的纵向联系,还要体现它们之间的横向联系,即不仅要建立章节之间知识点的外在联系,还要对本章的知识点建立内在联系．例如，高中知识点中的函数部分,它的思想方法是贯穿高中整个数学的学习过程,因此，在每个章节的学习中要经常与函数建立联系．经过这样的训练,学生就能对所学的知识点不单单是简单的记忆,而是有意识地去运用知识点,对知识点进行重组和概括,突出知识点的延伸功能,真正达到学有所用,为能熟练运用构造法解题打下坚实的基础．

3. 注重对学生发散性思维的培养

利用构造法解决数学问题时,需要学生多角度思考问题,多渠道解决数学问题,这些都需要学生具有发散性思维．在我们的实际教学中,我们可以从多方面进行发散思维的训练．比如，关注数学命题的发散,在不改变数学命题的本质的前提下,通过改变数学命题的条件,结论等,引导学生不断根据变化的情况积极的去思考、归纳、概括,从而达到多角度去看数学命题的本质.平时教学中，我们强调变式训练,就是对这方面的一个强化．关注学生解题方法的发散,对于学生碰到的同一个数学问题,要从多个角度进行研究和解决,对不同的数学问题要利用共同的方法进行解决；这个也是我们平时教学中强调的“一题多解”和“通性通法”的教学形式，这为学生进行构造法解题打下坚实的思维基础．

总之,在利用构造法解题的过程中,不仅要求学生会分析问题,解决问题,还需要学生有构造新问题的能力, 构造法解题过程就是一种探究,一种创新的思维过程,对学生的学习热情,进行自主学习能力的培养都是有着不可估量的作用．