多重随机环境中的马尔可夫链

费时龙

(宿州学院数学与统计学院,安徽宿州234000)

多重随机环境中的马尔可夫链

费时龙

(宿州学院数学与统计学院,安徽宿州234000)

引入了多重随机环境中的马尔可夫链,讨论了多重随机环境中的马尔可夫链的若干性质,给出了多重随机环境中的马尔可夫链的几个应用背景.证明了多重随机环境中的马尔可夫链的一个存在性定理,获得了多重随机环境中的马尔可夫链若干等价描述.

随机环境;多重马氏链;股市预测;人口预测

0 引言

马尔可夫链是随机过程中历史最悠久且至今仍然充满活力的一个分支.特别是对时间齐次的马尔可夫链(以下称为经典马氏链)的研究已取得了较为完善的结果,具有深厚的理论基础,在许多领域中有着广泛的应用背景,如现代物理、生物学、经济学、网络理论、保险学等.简单地说,经典马氏链主要是研究转移函数具有确定的情形;然而,现实世界中还大量存在着许多不确定情形,因此需要对经典马氏链模型进行推广.Cogburn首先考虑到转移函数会受到一个随机因素的干扰,引入了随机环境中的马尔可夫链(以下简称MCRE).自20世纪80年代以来,MCRE的理论得到了长足的发展,国内外许多学者对此进行了广泛的研究并取得了很多丰富的成果.刚开始的研究主要是集中在MCRE的两种特殊模型,即随机环境中的随机游动与随机环境中的分支过程,详见文献［1-6］.在此基础上,MCRE的一般理论的研究得到了较好的发展.Cogburn在MCRE的状态分类［7-8］、平稳分布［9］、中心极限定理［10］等方面获得了丰富的研究成果.Orey［11］对Cogburn等人的工作进行了总结和评价,同时得到类似于经典马氏链理论方面的结果并提出了一些公开的问题让大家研究解答.丁万鼎［12］研究了MCRE的构造并讨论了MCRE与马氏性的关系.胡迪鹤［13-14］分别讨论了MCRE的构造与随机环境中q-过程的存在唯一性.李应求［15-16］研究了MCRE与马氏双链的关系.关于MCRE的详细介绍可参考文献［17］.本文主要是在MCRE的研究基础上对MCRE模型进行推广,引入了多重随机环境中的马尔可夫链模型,讨论了多重MCRE的一些性质,给出了多重MCRE的一些应用.例1给出了多重MCRE在股市预测中的应用背景;例2给出了多重MCRE在人口预测中的应用背景;例3、例4给出了两种特殊的多重MCRE(二重随机环境中的随机游动);例5应用定理1.3的结果给出了多重MCRE在产品销售预测模型中的应用.

1 多重MCRE的模型与性质

(i)固定θm及xm,p(θm;xm,·)是A上的一个概率测度,

(ii)固定θm及A∈A,p(θm;·,A)关于Am可测,

(iii)固定xm及A∈A,p(·;xm,A)关于ßm可测,

(iV)对每个固定的A∈A,p(·;·,A)关于ßm×Am可测,

则称p(·;·,·)为一个m重随机马尔可夫核.

下面定理1.1将讨论m重随机环境中的马氏链的几个等价条件,定理1.2将给出随机环境中的马氏链、m重随机环境中的马氏链、n重随机环境中的马氏链之间的相互关系.

定理1.1下列条件等价.

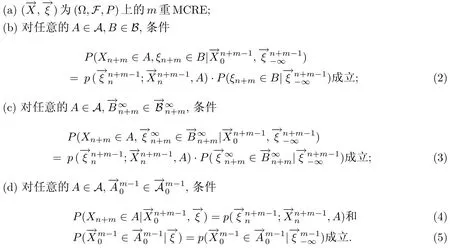
注1.2由注1.1及定理1.2知MCRE必然是m重MCRE,从而m重随机环境中的马尔可夫链是随机环境中的马尔可夫链模型的推广.它的直观想法为:系统未来(n+m时刻)的演变规律只与最近一段时间内(n时刻到n+m-1时刻)系统所处的状态和环境有关,而与过去较长时间(n时刻之前)无关.

下面给出该模型的几个应用背景.

例1(股票价格预测模型)设Xn,n=0,1,2,···表示在n时刻某种股票的价格.显然若不考虑环境因素的变化且假定未来的股票价格只与现在有关而与过去无关,则Xn为一个马氏链.一般的情况,若未来的股票价格不仅与现在有关,还与现在到过去一段时间(不妨设为m个单位时间)内的股票价格有关,则Xn为一个m重马氏链.更为一般的,若进一步考虑外部环境(如经济政策、公司经营状况、市场环境等因素)的变化,即假定未来的价格会受到一段时间(不妨设为m个单位时间)内外部环境的影响,则Xn为一个m重随机环境中的马氏链.因此,m重随机环境中的马氏链对于股票价格预测模型具有更符合实际的情形.

例2(人口预测模型)设Xn,n=0,1,2,···表示n时刻的人口数量.在理想的情况下,若假设未来的人口数量只与现在的人口数量有关,而与过去的人口数量无关,则Xn为一个马氏链.考虑到人的大致生育年龄段和死亡年龄段,假设未来的人口数量不仅与现在有关,还与现在到过去一段时间(不妨设为m个单位时间)内的人口数量有关,则Xn为一个m重马氏链.更为一般的,若进一步考虑自然环境因素的影响,即假定未来的人口数量会受到从现在到过去一段时间(不妨设为m个单位时间)内的自然环境的影响,则Xn为一个m重随机环境中的马氏链.因此,m重随机环境中的马氏链对于人口预测模型具有更合理的情形.

例3(空间随机环境中直线上二重紧邻的随机游动)设e={(ξi,ηi)}i∈Z为一列定义在概率空间(Ω,F,P)上取值于(0,1)2上的二维随机向量序列,若满足条件

则称{Xn,n≥0}为空间随机环境e中直线上二重紧邻的随机游动.

例4(时间随机环境中直线上二重紧邻的随机游动)例3中的转移函数是空间位置的随机变量函数,若将其替换成时间的随机变量函数,即满足条件

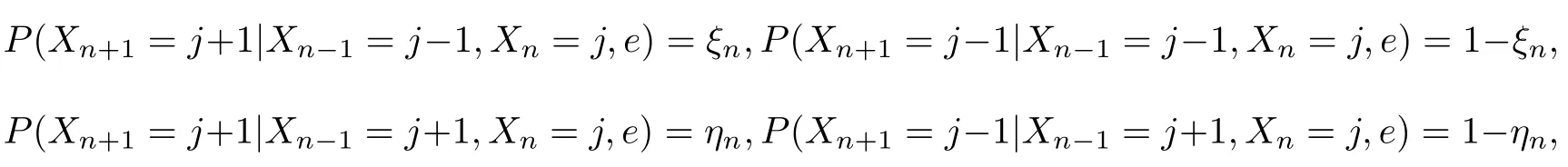
则称{Xn,n≥0}为时间随机环境e中直线上二重紧邻的随机游动.

下面定理1.3讨论m重随机环境中马尔可夫链的存在性,并讨论m重随机环境中的马氏链、m重马尔可夫链和马尔可夫链之间的相互关系.

由定理1.3中的(iV)与(V)知:通过扩大相空间维数的方法,我们可以利用m重马尔可夫链与马尔可夫链的相关理论工具研究m重随机环境中的马尔可夫链.下面给出该方法的一个应用.

例5(产品销售预测模型)企业在产品生产过程中需要对未来的销售情况进行预测,以便为企业的生产规模提供合理的理论依据.为简单起见,现将销售状态看成两种情形:以“Xn=1”表示在n时刻产品“畅销”;以“Xn=0”表示在n时刻产品“滞销”.再将市场环境状态也看成两种情形:以“ξn=1”表示在n时刻市场环境“良好”;以“ξn=0”表示在n时刻市场环境“恶化”.显然若不考虑市场环境序列的变化(即将市场环境序列固定),且未来的销售状态只与当前的销售状态有关,则{Xn,n≥0}为一个马氏链.但更一般的情况,若市场环境序列{ξn,n≥0}是随机变化的,且未来的销售状态不仅与当前的销售状态有关,还与当前到过去的m个单位时间销售状态及市场环境有关,则可将{Xn,n≥0}看成是m重随机环境{ξn,n≥0}中的马氏链,从而多重随机环境中的马氏链具有更广泛的适用范围.下面利用定理1.3的有关性质给出求P(Xn+1=1)及P(Xn+1=0)的方法.

求解方法不失一般性,不妨设m=2,并假定环境序列{ξn,n≥0}为时齐的2重马氏链.我们可以通过对市场调查获得其转移概率(如通过转移频数近似转移概率),设为

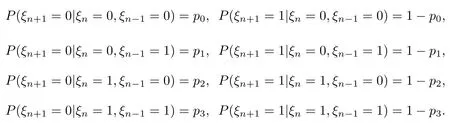
由于{ξn,n≥0}为具有2个状态的时齐的2重马氏链,故{(ξn+1,ξn),n≥0}为一个具有4个状态的时齐的马氏链.利用二进制的方法可将{(ξn+1,ξn),n≥0}的4个状态分别对应为:(0,0)↔0,(0,1)↔1,(1,0)↔2,(1,1)↔3,其转移概率矩阵为

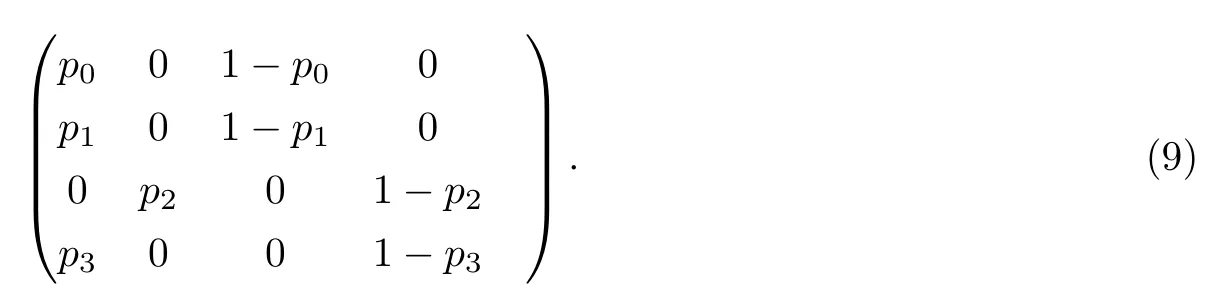
由转移概率矩阵(9)及{(ξn+1,ξn),n≥0}的初始分布((ξ1,ξ0)的分布),并再利用马氏链的相关理论即可求出(ξn+1,ξn)的分布,进而由关系式

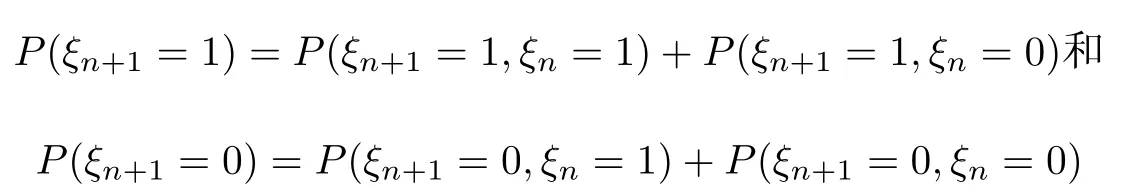
即可求出ξn+1的分布.同理,我们可以通过对历史数据的调查获得如下的转移概率.设

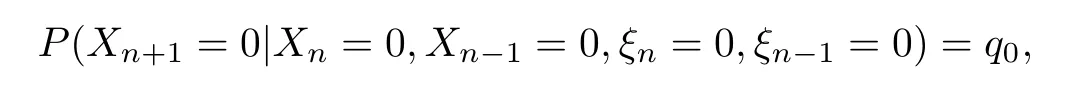
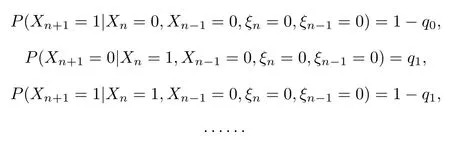
再根据定理1.3知{(Xn+1,Xn,ξn+1,ξn),n≥0}为一个具有16个状态的时齐的马氏链.我们可以利用上式获得其转移概率矩阵,再根据{(Xn+1,Xn,ξn+1,ξn),n≥0}的初始分布即可求出{(Xn+1,Xn,ξn+1,ξn),n≥0}的分布.从而利用全概率公式便可得到P(Xn+1= 1)及P(Xn+1=0)的求解公式(这里由于转移概率矩阵形式较复杂,省略具体求解表达式).

2 定理的证明

本节将给出定理1.1、定理1.2、定理1.3的证明,首先给出下列引理.

引理2.1［17］设(Ei,εi)为可测空间,Wi是概率空间(Ω,F,P)上的Ei值随机元(i= 1,2,3),fi是Ei上的有界可测函数(i=1,2,3),C是F中的子σ-代数,W1与W2关于C条件独立,W3关于C/ε3可测,f3是(E2×E3,ε2×ε3)上的有界可测函数,则

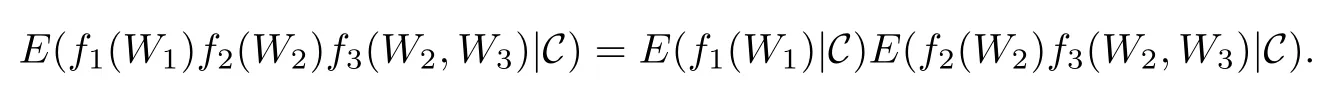
定理1.1的证明(a)⇐⇒(b)由定义1.2显然,下证(b)⇒(c).设

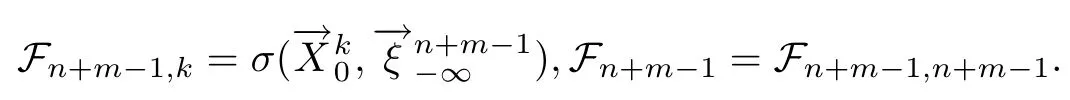
首先证明对任意的k≥1,有

这里A∈A,Bi∈ß,1≤i≤k,n≥0.应用数学归纳法证明式(10)、式(11).当k=1时,在式(2)中令A=χ可得式(10)成立.将k=1时的式(10)的结论代入式(11),可得当k=1时式(11)成立.设式(10)、式(11)对k成立,则对k+1时,有

由式(2)和注1.2得

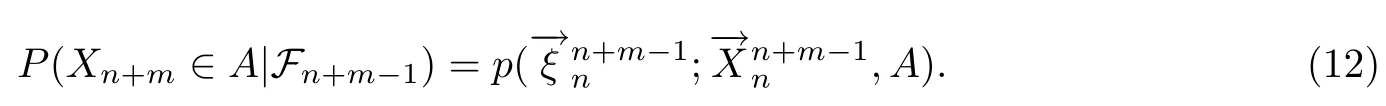
由归纳假设的式(10)对k成立知{ξn+m,···,ξn+m+k-1}与{X0,···,Xn+m-1}关于条件独立.由式(11)对k成立及式(12)可知{ξn+m,···,ξn+m+k-1}与Xn+m关于Fn+m-1条件独立.现将Xn+m看成引理2.1中的W1,将{ξn+m,···,ξn+m+k-1}看成引理2.1中的W2,将看成引理2.1中的W3,将Fn+m-1看成引理2.1中的C,则由引理2.1可得

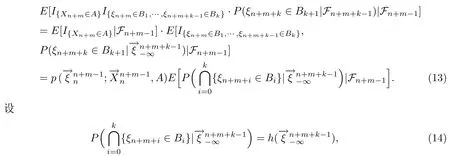
利用式(12)、式(13)、式(14)、式(15)式可得

特别地,在式(16)中令A=χ得式(10)对k+1成立,将式(10)对k+1成立的结论带入式(16)可得式(11)对k+1也成立,从而式(10)、式(11)成立.由式(10)和式(11)可得对中的所有柱集,式(3)成立,由单调类定理易证明式(3)成立.

再令A=χ得

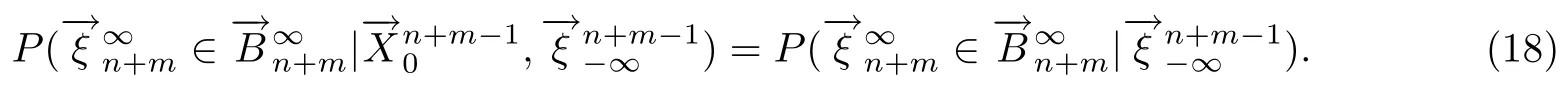
由式(17)和式(18)易得式(4)成立.在式(18)中令n=0得式(5)成立,故(c)⇒(d)得证.

下证(d)⇒(b).设式(4)和式(5)成立,则对k＜n及有界可测函数f,有

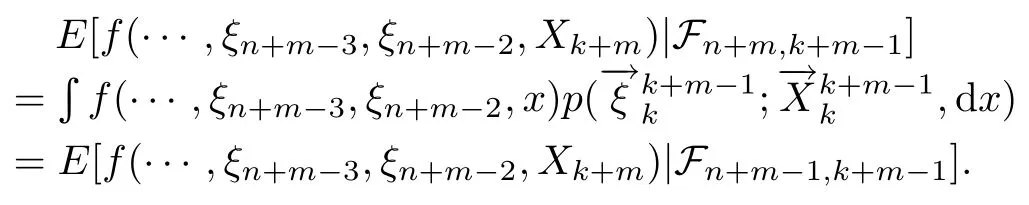
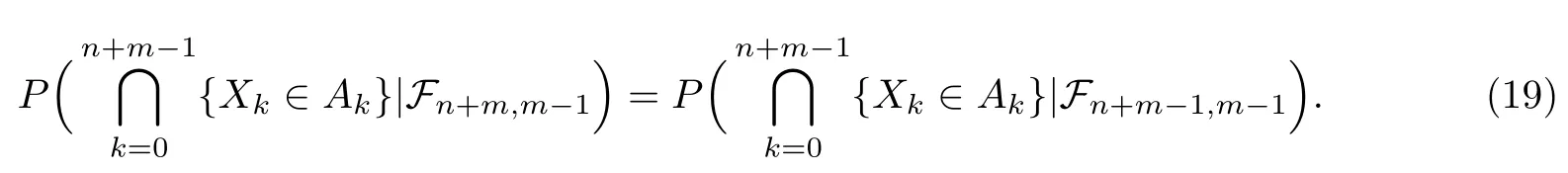
利用式(5),对有界可测函数g,h,有

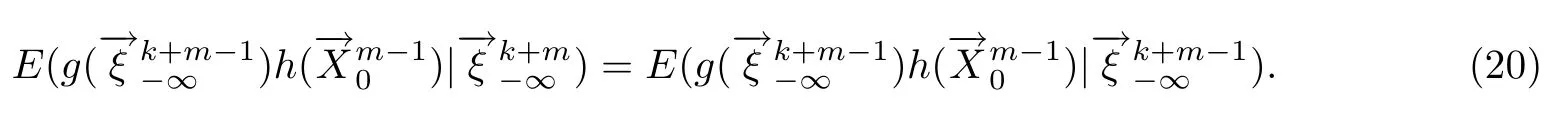
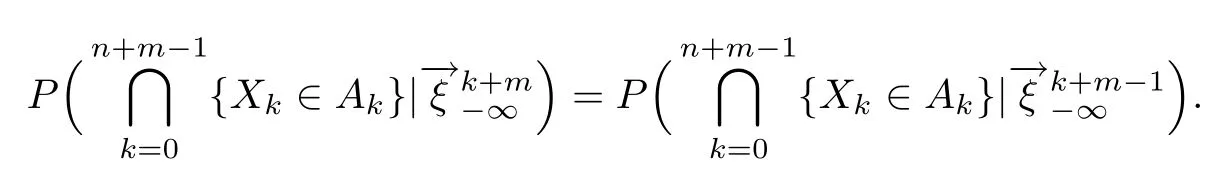
故ξk+m与{X0,X1,···,Xn+m-1}关于条件独立.因此

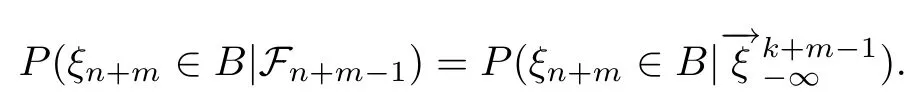
从而有

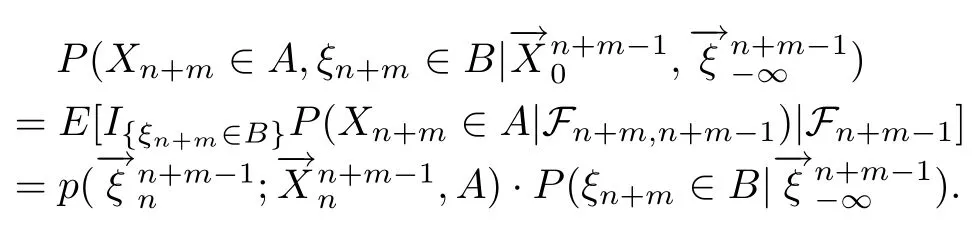
故(d)⇒(b)得证.

定理1.2的证明若p(·;·,·)为一个m重随机马尔可夫核,则记

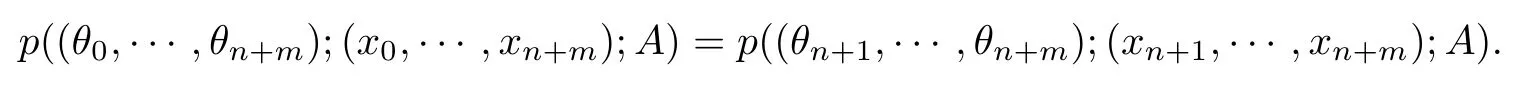
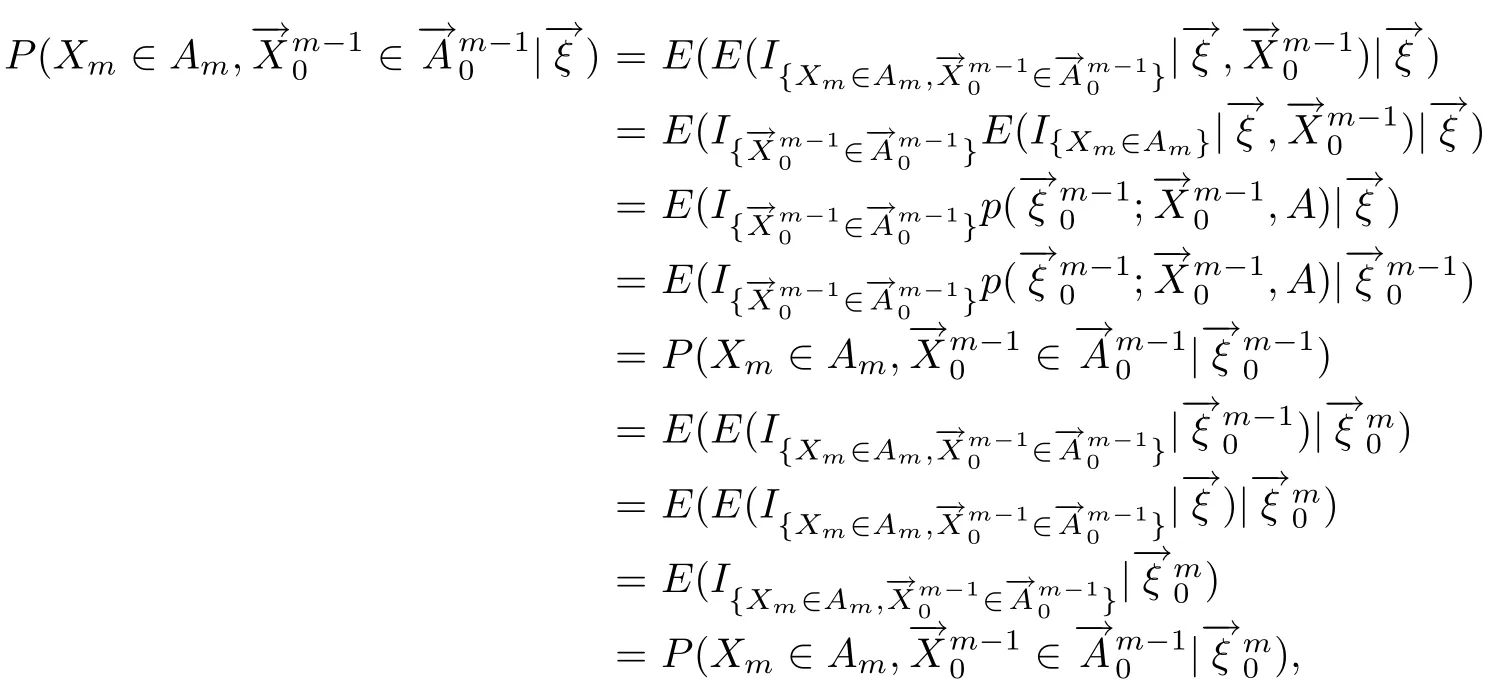
［1］SZASE D, TOTH B. peresist random walks in one-dimensional random environment ［J］. Journal of Statistical physics, 1984, 37(1): 28-38.

［2］SOLOMN F. Random walks in a random environment ［J］. Ann probab, 1975, 3(1): 1-31.

［3］KOZLOV M V. On the asymptotic behavior of the probability of non-extinction for critical branching processes in a random environment［J］. Theory prob Appl, 1976, 21(4): 742-751.

［4］ALILI S. persistent random walks in stationary environment ［J］. Journal of Statistical physics, 1999, 94(3):469-494.

［5］SMITH W L, WILKINSON W E. On branching processes in random environments ［J］. Ann Math Statist, 1969,40(3): 814-827.

［6］胡杨利,吴庆平,李应求.随机环境中依赖年龄分枝过程的爆炸问题［J］.数学学报A辑,2010,53(5):1027-1034.

［7］COGBURN R. Markov Chains in random environments［J］. Ann probab, 1980, 8(3): 908-916.

［8］COGBURN R. The ergodic theory of Markov chains in random environments［J］. Z W, 1984, 66(2): 109-128.

［9］COGBURN R. On direct convergence and periodicity for transition probabilities of Markov chains in randomenvironments［J］. Ann probab, 1990, 18(2): 642-654.

［10］COGBURN R. On the central limit theorem for Markov chains in random environments［J］. Ann probab, 1991,19(2): 587-604.

［11］OREY S. Markov chains with stochastically stationary transition probabilities［J］. Ann probab, 1991, 19(3):907-928.

［12］丁万鼎.关于随机环境中的马尔可夫链的马氏性［J］.安徽师大学报,1986,(4):1-5.

［13］胡迪鹤.随机环境中q-过程的存在唯一性［J］.中国科学A辑,2004,34(5):625-640.

［14］胡迪鹤.从P-m链到随机环境中的马氏链［J］.数学年刊A辑,2004,25(1):65-78.

［15］李应求.关于马氏环境中马氏链的几点注记［J］.数学进展,1999,28(4):358-360.

［16］李应求.随机环境中马氏链与马氏双链间的相互关系［J］.数学学报,2006,49(6):1373-1380.

［17］胡迪鹤.随机环境中的马尔可夫过程［M］.北京:高等教育出版社,2011.

(责任编辑李艺)

The multiple Markov chains in random environments

FEIShi-long
(School of Mathematics and Statistics,Suzhou University,Suzhou Anhui 234000,China)

The multiple Markov chains in random environments were introduced and several properties and application backgrounds of the multiple Markov chains in random environments were given.An existence theorem on the multiple Markov chains in random environments was p roved and several equivalent conditions of the multiple Markov chains in random environments were presented.

random enveronments;the multiple Markov chains;stock market prediction;population prediction

O 211.62

A

10.3969/j.issn.1000-5641.2016.01.010

1000-5641(2016)01-0081-10

2014-12

高校优秀青年人才支持计划重点项目(gxyqZD2016340);安徽省自然科学研究项目(KJ2013 B288);宿州学院青年人才基金(2013XQRL04);安徽省创新训练项目(AH201410379079, AH201410379077)

费时龙,男,硕士,讲师,主要研究方向为概率论与数理统计.E-mail:fsl627@sina.com.