等腰三角形解题中的基本模型及应用
王莉莉
(浙江省绍兴市新昌县西郊中学,浙江新昌 312500)
引 言
等腰三角形是初中几何知识的入门图形,也是进一步研究几何知识的重要基础,在中考中有着举足轻重的地位,无论填空题、选择题、解答题,都离不开这一核心知识的考查。但学生在初次涉及这类题型时,往往会对复杂多变的图形感到迷惑,一头雾水,无从下手。其实,不管如何复杂的图形,本质上都是由几个基本图形组合而成。因此,学会了剥离复杂图形,掌握等腰三角形基本解题模型,解题自然水到渠成了。
一、等腰三角形基本解题模型
就八年级等腰三角形知识章节,笔者总结出如下四种解题时常用的模型。
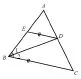
图1 角平分线+平行线模型
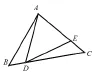
图2 手拉手共边模型
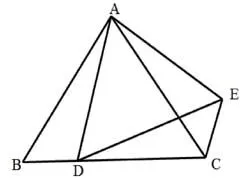
图3 手拉手共顶点模型
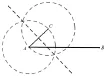
图4 两圆一中垂模型
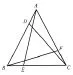
图5 等腰(边)三角形类弦图模型
【模型1】角平分线+平行线模型,如图1。该模型特征展示了等腰三角形底角平分线和过平分线一点平行底边的直线。
【模型2】手拉手共边(顶点)模型如图2、图3。该模型分两类:(1)两等腰三角形一腰重叠;(2)两等腰三角形一顶点重合后旋转任意角度变换得到多种图形。
【模型3】两圆一中垂模型,如图4。该模型条件给出两定点和一定直线,要求在直线上找一动点满足构成等腰三角形。
【模型4】等腰(边)三角形类弦图模型,如图5。该模型是以等边三角形为背景图,各边截取等长线段构造全等三角形和新的正三角形,同时也可以省略部分线段拓展更多图形。
二、等腰三角形模型的应用
(一)角平分线+平行线模型
例1.如图6,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E,交AC于F,AB=9,AC=8。求:(1)图中有几个等腰三角形;(2)AEF的周长,并说明理由。
分析:问题(1)的解题本质在于发现角平分线+平行线会产生多个相等的角,且根据同一三角形中等角对等边的性质可以得到多个等腰三角形。
问题(2)中根据线段之间的等量替换,能够顺利将第二个求周长问题转化为已知线段和的问题。因此,利用该模型解题效果事半功倍。

图6
(二)手拉手共边(顶点)模型
1.手拉手模型之一等腰三角形+等腰三角形(一腰重叠)
例2.如图7,在等腰ΔABC中,AB=AC。
(1)AD是BC上 的 高 线,E是AC上一点,且AE=AD,若∠BAD=30°, 则∠EDC=____________ 。
(2)AD是BC上 的 高 线,E是AC上一点,且AE=AD,若∠BAD=40°,则∠EDC=_____________ 。

图7
(3)思考:通过以上两题,你发现∠BAD 与∠EDC之间有什么关系?用等式表示。
(4)如果AD不是BC上的高线,AD=AE,那么∠BAD 与∠EDC之间是否仍有上述关系?请说明理由。
分析 :问题(1)(2)通过已知一个角的度数和等腰三角形等边对等角、三线合一性质可快速解题。问题(3)给定具体的角度,通过直观观察两角之间的数量关系可以归纳角与角之间的特殊规律,学生易得出结论。
问题(4)条件由特殊向一般改变,进一步弱化条件,引导学生揭示这一类基本图形具有的特殊规律,利用模型得出一般结论:两个等腰三角形,一腰重叠则∠BAD =2∠EDC。
2.手拉手模型之二等腰三角形+等腰三角形(一顶点重叠)
例3.在等腰ΔABC中,AB=AC,D是BC上一点(不与B、C重合),以AD为一边在AD的右侧作三角形ADE,使AD=AE,∠DAE=∠BAC,连结CE。
(1)如图8,若∠BAC=90°,①求证ΔABD≌△ACE;②求∠BCE的度数。
(2)设∠BAC=α,∠BCE=β,如图9,猜想α、β之间的数量关系,并予以证明。
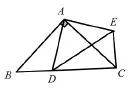
图8
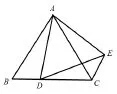
图9
分析:以上两个问题的解决都需要抓住图形变化中ΔABD≌△ACE的不变性。两个等腰三角形在共顶点模型中因为对应角度的和差相等关系不变,所以应用(SAS)的全等判定方式判定全等不会改变。即使将两个等腰三角形绕共点A旋转任意角度,构造更为复杂的图形,它们仍具有全等不变的事实。通过应用模型得出一般结论:两个顶角相等的等腰三角形,顶点重合,三角形全等,∠BAC +∠BCE=180°。结合全等三角形的知识,教师可引导学生体会知识的相辅相成。
(三)两圆一中垂模型
例4.如图,在△ABC中,AB=AC,∠B=2∠A。
(1)求∠A和∠B的度数。
(2)BD是△ABC中∠ABC的平分线。①写出图10中与BD相等的线段,并说明理由。②直线BC上是否存在其他的点P,使△BDP为等腰三角形?如果存在,在图11画出所有满足条件的点P,并直接写出对应的∠BDP的度数;如果不存在,请说明理由。
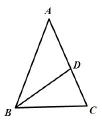
图10

图11
分析:本题第一小题考查等腰三角形边角对应的性质,学生容易解题。第二题是对等腰三角形有关边、角基础性质的提高,是易错题。我们可以通过图11的模型帮助学生寻找点P。当BD是三角形的腰时,以点B为圆心,BD长为半径画圆,交直线BC与P1、P2;以D为圆心,BD长为半径画圆,交直线BC于P3;当以BD为底时,作BD的中垂线与BC相交与P4。学生在解题中如果忽略对等腰三角形腰、底角不确定时的合理分类讨论,就容易出现错误。因此,解题时教师应帮助学生建立两圆一中垂的分类讨论模型,这样就能轻松解决以边、角不明确为共性的问题。
(四)等腰(边)三角形类弦图模型
例5.如图12,点M、N分别在正△ABC的边BC,AC上,且BM=CN,AM、BN交于点Q。
(1)求证∠BQM=60°。
(2)若将题中“BM=CN”与“∠BQM=60°”的位置交换,得到的是否仍是真命题?
(3)若将题中的点M,N分别移动到BC,CA的延长线上,是否仍能得到∠BQM=60°?
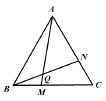
图12
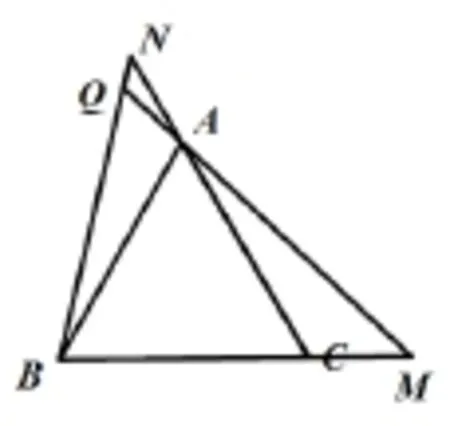
图13
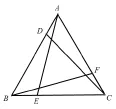
图14
分析:问题(1)是由图14隐藏了线段CD改编而来,在图14中我们利用等边三角形的旋转对称性,根据(SAS)判定△ABE≌△BCF≌△CAD,再利用外角的性质得到新构成的三角形仍为正三角形。解答这道题的关键是利用图14模型得到△ABM≌△BCN,同样利用外角性质得出∠BQM=60°的结论。问题(2)的条件结论互换不会影响解题的本质方法。问题(3)是问题(2)的拓展,解答时应抓住当点M、N分别移动到BC、CA的延长线上时,△ABM≌△BCN仍满足。因此,在等边三角形类弦图的大框架下,改变部分条件,拓展延伸的问题,仍可借鉴此模型解题,教师可引导学生体会万变不离其宗的意义。
结 语
苏霍姆林斯基认为:“教给学生方法比教给学生知识更重要。”提炼基本模型是知识升华的过程。从上述例题中可以发现,等腰三角形的有关证明题采用模型角度进行分析,便能降低解题难度。因此,理解和掌握以上所列举的等腰三角形模型,对用等腰三角形知识的解题具有重要意义。它能促使学生更准确地把握图形本质,促使学生更合理地找到解决问题的方向,促使学生生成更有效的学习方法[1]。
当然,在等腰三角形的相关解题过程中,运用模型时要灵活变通,不可过度依赖、生搬硬套,把模型固定化,把解题思路僵化。同时,我们在解题过程中可提炼的模型并不只有以上几种,图形千变万化,知识层层叠加,我们只有以等腰三角形基本性质为基础,以基本模型为生长点,多观察、多思考、多类比、多提炼总结,才能提高数学学习的有效性。

