考虑参数不确定性的板结构振动响应统计分析
张艾萍, 李亚轩, 肖 斌, 石双霞, 曹丽华, 高 超, 邱 瑞
(1.东北电力大学 能源与动力工程学院,吉林 吉林 132012;2.中国电力工程顾问集团 东北电力设计院有限公司,长春 130021)
实际工程结构中,由于系统参数、外部激励以及边界条件等一系列不确定性因素,致使系统的固有特性、动态响应与频响特性等[1-3]具有随机性特征。随着工程中向复杂化和高精度方向的飞速发展,传统上忽略或简化这些因素的确定性结构分析方法,不再能满足客观要求,因此有必要将其纳入到系统响应分析过程中。
近年来针对结构振动的动力学分析[4-5]是该领域的热点问题,但在过程中引入不确定性因素的分析技术尚未成熟,其中:MCS(Monte Carlo Simulation)方法[6]从统计的角度出发,给出了随机系统一种统计分析方法,但对于大型复杂结构系统,因其工作量繁重而往往不被采用;而从动力学基本原理出发,辅以数学理论方法进行不确定性分析,也可得到较精确结果。梁震涛等[7]利用随机因子法与代数综合法计算了板梁组合结构响应的均值、方差表达式,指出随机性与确定性模型的分析结果确有差异。Adhikari[8]基于随机矩阵理论提出了量化悬臂板的质量、刚度和阻尼不确定性矩阵变量分布,分析宽频范围内系统动态响应。李舜酩等[9]以Lagrange动力学方程和Rayleigh-Ritz能量法为理论基础,建立了随机质量板的随机振动方程,实现振动响应的统计特性分析。王凤阳等[10]将摄动理论与虚拟激励法相结合,讨论了随机荷载激励下不确定参数结构的随机响应统计特征。此外,还有学者提出了精细积分法[11]及其改进[12],也可得到结构随机振动响应的概率统计特性。
上述MCS方法及其它结合数学理论改进方法皆是以相关动力学方程为出发点,而本文则从另外一个角度出发求解系统随机响应,即:只需明确系统各不确定性因素,基于概率统计特性与正交多项式理论逼近随机响应,并结合FEA计算,利用Fourier-Hermite多项式展开、广义模型降维和多重Gauss-Hermite数值积分,获得板结构单点激励作用下稳态振动响应的显示多项式函数形式,继而得出其概率统计特征,并基于此对弹簧支撑离散随机刚度边界条件下系统随机响应开展统计分析,这将对研究板结构等典型系统的随机动力学响应与传递方面具有一定的探索意义。
1 基本原理
对于一个给定的线性多自由度结构系统,其在载荷激励下的动力学基本方程[13]可表示为

(1)

当系统忽略阻尼或在比例阻尼条件下,质量矩阵M、阻尼矩阵C和刚度矩阵K均为对称实数矩阵。在模态坐标解耦条件下,应用模态叠加原理,可得单点激励下原点p处响应为
(2)
式中:Mr、Cr和Kr分别为模态坐标下的模态质量、模态阻尼和模态刚度;φpr和fp(ω)分别为激振点p处第r阶模态频率对应的模态向量和激振力。
考虑系统具有变边界条件,由于存在系统不确定性,导致上式中模态刚度具有不确定性。此时,系统响应也具有随机性,可表示为
(3)
式中:x1,x2,…,xN分别为系统变边界条件下的各个随机参数变量;显然,在给定激励频率ω下,系统p处原点响应成为随机参数变量的函数。
然而,仅应用上述动力学理论推导,难以实现对系统响应结果的预测。
2 系统振动响应统计分析
2.1 Fourier-Hermite多项式展开
采用高维模型[14],可将任意一个连续、可微的多变量函数按照各随机参数进行有限变量的层次函数展开,故式(3)可表示为
(4)
式中:x={x1,x2,…,xN}T∈RN为N维空间随机参数向量;y0为一个实常数;yi1…iS(xi1,…,xiS)为任意S(S≤N)个随机参数xi1,…,xiS间耦合作用对多变量响应函数y(x)的贡献量。
针对式(4),考虑各随机变量均服从相应的正态分布时,进行Fourier-Hermite多项式展开,得到y(x)的S个变量函数逼近形式,其表达式为[15]

(5)
式中:多项式展开系数

(6)
式中:fk(xk)为单个随机参数xk的概率密度函数;fX(x)为各随机参数的联合概率密度函数;ψj(xi)为以xi为自变量的第j阶Hermite多项式函数;m为选取Hermite多项式的最高阶数,j≤m。

2.2 广义模型降维
多维变量函数的广义降维法由Xu等[16]提出,以结构概率特性分析为出发点,将多变量函数以排列组合的方式展开为
(7)
式中:R为y(x)多项式展开的变量元数,R≤N;y(xk1,xk2,…,xkR-k)中未标明的变量取各自均值。
将式(7)代入式(6)可得多项式展开系数

(8)
以及均值
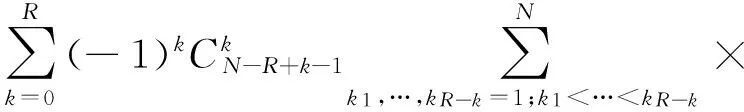
(9)
从式(9)可以看出,引入广义降维法将N维积分进行积分降维,将大大提高多项式展开系数及均值的计算效率,尤其在S< 针对Hermite多项式的多重Gauss-Hermite求积公式为 (10) 式中:n1,…,nS分别为相应变量xi1,…,xiS所选取积分节点的数目;Wk为各个变量相应积分节点xk处的求积系数。针对含有e-x2特殊项的积分问题,式(10)可将其转化为累加和的形式,可以更为方便和快捷地求解多项式展开系数与均值。 为提高式(10)的计算精度与效率,可令n=n1=…=nS。 (11) 在简谐激励下,矩形板结构在两侧自由、左边固支-右边弹簧支撑边界条件下,受到单点简谐力激励起原点振动,其FEM模型如图1所示。对此,利用文中提出的方法,针对稳态激励原点处z方向振动位移响应,获得其系统随机响应统计特征。 图1 矩形钢板简图 该钢板的结构设计参数分布如表1所示。激励方式为单点正弦载荷激励,且激振力幅值F=1 000 N,作用于钢板右上方长、宽各1/3处,即图1中所示的网格节点上。仿真分析时,为了研究变弹簧支撑边界条件下钢板的振动响应特性,假设钢板右端边界条件处总刚度均值及其变异系数保持不变且均匀分布于网格节点上;钢板右端所有支撑弹簧的刚度系数可看作不确定性因素,均服从相互独立的高斯分布。 表1 结构设计参数分布 对工程结构进行FEM分析时,网格单元尺寸的选取将对结构系统响应求解结果的精确性产生直接影响,因此有必要选取一定的划分标准。韩增尧[17]最先以波动理论为基础,提出了针对具体结构的网格单元划分标准。对于平板,网格单元尺寸要求如下[18] (12) 式中:δ为平板厚度;E为平板材料的弹性模量;μ为泊松比;ρ为质量密度;λ为平板的弯曲波波长;fmax为所考虑的频率范围上限。 利用ANSYS有限元软件对各参数均取其均值的板结构模型进行谐响应分析,可得钢板在0~100 Hz频率范围内激励点处的z方向位移级谱,如图2所示。 图2 激励点处z方向振动响应的位移级谱 Fig.2 Displacement level spectrum ofzdirection vibration response at the driving point 在第二阶固有频率(22.57 Hz)与第三阶固有频率(32.166 Hz)之间选取25 Hz作为激励频率进行后续单频稳态受迫振动分析。采取1.0×105次直接MCS模拟对上述具有k1~kn随机刚度系数变量的矩形钢板结构进行单频谐响应分析计算,其激励点处z方向的振动位移响应幅值样本分布及其概率密度曲线如图3所示。 以ANSYS软件作为求解器,根据本文提出的Fourier-Hermite多项式展开式(5)进行振动位移响应分析,其中Gauss-Hermite求积公式选取n=7个积分节点和m=5阶Hermite多项式,在此基础上嵌入1.0×105次局部MCS模拟,分析系统激励点处z方向的振动位移响应幅值统计特征,其结果如图4所示,其中包括单变量、双变量和三变量的z方向位移幅值显示化多项式函数逼近统计结果。由图4可知,z方向位移幅值的单变量结果与双变量、三变量以及直接MCS模拟结果相比具有一定程度偏差,这是由于其忽略了两个及以上变量之间的耦合作用对响应结果的贡献,但实际上它们亦对系统位移响应具有一定影响。而采用双变量与三变量时位移响应的概率密度曲线近似重合,而且能极为准确地反映出直接MCS模拟柱状图的分布规律,说明三个以及更多随机变量间耦合作用对位移响应的贡献较小。 图3 激励点处z方向振动位移响应幅值的样本分布 表2给出了单点正弦载荷激励下激励点处z方向位移响应幅值由式(11)所求得的误差分析结果,以更为直观的方式说明了上述分析结果的正确性。工程上对于计算精度一般要求小于等于5%,可知本例中板结构位移响应的单变量、双变量和三变量逼近均已在误差允许范围内,但单变量响应逼近统计结果的各阶矩误差相对于双变量、三变量来说均较大,可见精确度仍不够高。尽管双变量和三变量响应逼近统计结果仍分别具有一定差别,但与单变量和双变量的差别相比较来看已经很小,说明三个以及更多随机变量间的耦合作用可以忽略不计。再者,文中仅针对板结构基础单元,对于实际中复杂结构由于误差的累积必然导致误差进一步加大。综上所述,在计算精准度以及工作量大小的权衡考虑下,双变量逼近该例中系统响应结果较为合适。 表2激励点处z方向振动位移幅值的误差分析 Tab.2Erroranalysisofzdirectionvibrationdisplacementamplitudeatthedrivingpoint% 误差一阶矩二阶矩三阶矩四阶矩单变量0.015850.065440.178640.38416双变量0.002800.006600.013540.02635三变量0.002330.004240.005910.00756 为了更为准确地获得变边界条件下板结构原点响应的统计特征,对平板网格做出如下调整:在长度方向满足以波动理论为基础的网格划分标准下,将网格单元长宽比[19]控制在1.5以内进行网格细化,具体划分情况如表3所示,其它未标明的结构设计参数由表1提供,且激振点的位置保持不变。以双变量逼近作为系统振动响应幅值的准确值进行对比分析。 表3 网格划分详细信息 图5给出了在节点弹簧数分别为7、10和13边界条件下,同一激励点处z方向的振动位移响应幅值概率统计特征。由该图可以看出三种边界条件下位移幅值概率密度曲线的趋势基本一致,均服从正态分布;但节点弹簧数为7时,由于宽度方向网格划分与式(12)相悖,导致位移幅值概率密度曲线反映出的均值及分布规律与其它两种边界条件相比差异明显;而节点弹簧数为13时的概率密度曲线与节点弹簧数为10时相比均值几乎相同,但方差有所减小,说明在板结构右端处于弹性离散边界条件下及总刚度不变时,随着离散节点弹簧变量的增加,随机响应结果的概率统计有向均值处聚拢的趋势。 为此,在板结构有限元网格满足划分标准前提下,进一步对长度和宽度方向网格进行细化,获得节点弹簧数分别为10,13,16和19边界条件下系统位移响应幅值概率统计特征,如图6所示。由该图可以看出,随着FEM网格细化,尽管所考虑的节点弹簧变量数逐渐增加,但激励点处随机位移响应幅值的均值大致相同,仅方差呈现减小趋势。可见,考虑板结构右端在随机离散刚度边界条件及总刚度一定的情况下,随着离散节点弹簧变量的增加,随机响应结果的概率统计有进一步向均值附近聚拢的趋势;但是这种趋势在逐渐地减弱,当节点弹簧数量趋近无穷时,即当板右端处于弹性连续边界条件,随机响应结果概率统计将满足某一定分布。 图5 不同边界条件下z方向振动位移响应幅值的统计结果 Fig.5 Statistical results ofzdirection vibration response amplitude under different boundary conditions 图6 不同边界条件下z方向振动位移响应幅值的变化趋势 Fig.6 The change trend ofzdirection vibration displacement response amplitude under different boundary conditions 本文结合Fourier-Hermite多项式展开、广义模型降维法以及Gauss-Hermite数值积分,提出了一种关于结构系统随机响应统计特征的分析方法,并结合网格划分技术对系统响应的预测结果进一步对比分析。主要结论如下: (1)随着考虑系统随机变量元数的增加,其系统稳态位移幅值响应统计特征将更加符合直接MCS模拟求解结果,但调用有限元次数与计算成本也将随之呈多项式增长,故应当根据误差分析选择适当随机变量元数,以在满足精度前提下尽可能减少计算工作量。 (2)当考虑随机参数变量个数较多时,采用文中方法仍可获得较高的计算效率和求解精度。 (3)本文并未假定系统稳态位移响应服从某一特定分布,故该方法适用性强。 (4)对网格逐步细化及离散节点弹簧数渐增的分析结果表明,FEM随机响应统计分布将向均值附近聚拢,且趋于连续随机刚度边界条件的某一确定分布。 然而,目前存在的不足之处是,当板结构右端处于弹性连续随机刚度边界条件时,建模以及响应逼近求解过程的工作量均将大大增加,需借助理论分析来进一步完善;再者,文中仅针对单点单频激励下板结构原点稳态振动随机响应的分析,对于跨点响应分析亦需进一步拓展研究。 参 考 文 献 [1] ADHIKARI S, FRISWELL M. Random eigenvalue problems in structural dynamics[J]. International Journal for Numerical Methods in Engineering, 2004, 69(3): 562-591. [2] 高伟,陈建军,马娟,等. 平稳随机激励下线性随机桁架结构动力响应分析[J]. 振动工程学报,2004,17(1):44-48. GAO Wei, CHEN Jianjun, MA Juan, et al. Dynamic response analysis of linear stochastic truss structures under stationary random excitation[J]. Journal of Vibration Engineering, 2004, 17(1): 44-48. [3] 高超,李亚轩,肖斌,等. 考虑参数不确定的系统固有频率统计分析[J]. 现代振动与噪声技术,2017(12):609-616. GAO Chao, LI Yaxuan, XIAO Bin, et al. Statistical analysis of natural frequency of the system with parameter uncertainties[J]. Modern Vibration and Noise Technology, 2017(12):609-616. [4] 蒲育,滕兆春,赵海英. 四边弹性约束矩形板面内自由振动的DQM求解[J]. 振动与冲击,2016,35(12):55-60. PU Yu, TENG Zhaochun, ZHAO Haiying. In-plane free vibration analysis for rectangular plates with elastically restrained edges by differential quadrature method[J]. Journal of Vibration and Shock, 2016, 35(12): 55-60. [5] 刚宪约,李丽君,柴山,等. 求解运动激励结构动态响应的固定边界-模态叠加法[J]. 机械工程学报,2016,52(13):87-93. GANG Xianyue, LI Lijun, CHAI Shan, et al. Fixed boundary mode superposition method for the dynamic analysis of base motion excited structures[J]. Chinese Journal of Mechanical Engineering, 2016, 52(13): 87-93. [6] HURTADO J E, BARBAT A H. Monte Carlo techniques in computational stochastic mechanics[J]. Archives of Computational Methods in Engineering, 1998, 5(1): 3-29. [7] 梁震涛,陈建军,马洪波. 随机参数板梁组合结构有限元分析的随机因子法[J]. 西安电子科技大学学报,2005,32(2):201-205. LIANG Zhentao, CHEN Jianjun, MA Hongbo. Random factor method of finite element analysis for random plate-beam composite structures[J]. Journal of Xidian University, 2005, 32(2): 201-205. [8] ADHIKARI S. Matrix variate distributions for probabilistic structural dynamics[J]. AIAA Journal, 2007, 45(7): 1748-1762. [9] 李舜酩,廖庆斌,尚伟燕. 随机质量板的振动响应及其统计分析[J]. 振动工程学报,2009,22(1):60-64. LI Shunming, LIAO Qingbin, SHANG Weiyan. Analyses of vibration responses and its statistical characteristics for random mass plate[J]. Journal of Vibration Engineering, 2009, 22(1): 60-64. [10] 王凤阳,赵岩,林家浩. 参数不确定结构平稳随机响应虚拟激励摄动方法[J]. 大连理工大学学报,2011,51(3):320-325. WANG Fengyang, ZHAO Yan, LIN Jiahao. Pseudo-excitation perturbation method for stationary random response of structure with uncertain parameters[J]. Journal of Dalian University of Technology, 2011, 51(3): 320-325. [11] 张森文,曹开彬. 随机振动响应计算的精细积分时域平均法[J]. 振动工程学报,1999,12(3):367-373. ZHANG Senwen, CAO Kaibin. Time-domain averaging of precise integration method for response of random vibration[J]. Journal of Vibration Engineering, 1999,12(3): 367-373. [12] 宋向华,安伟光,蒋运华. 任意随机激励下结构随机振动分析的一种数值方法[J]. 振动与冲击,2013,32(13):147-152. SONG Xianghua, AN Weiguang, JINAG Yunhua. A numerical method for random vibration analysis of structures under arbitrary random excitations[J]. Journal of Vibration and Shock, 2013, 32(13): 147-152. [13] 傅志方. 振动模态分析与参数辨识[M]. 北京:机械工业出版社,1990. [14] RABITZ H, ALIÖ F. General foundations of high-dimensional model representations[J]. Journal of Mathematical Chemistry, 1999, 25(2/3): 197-233. [15] RAHMAN S. A polynomial dimensional decomposition for stochastic computing[J]. International Journal for Numerical Methods in Engineering, 2008, 76(13): 2091-2116. [16] XU H, RAHMAN S. A generalized dimension-reduction method for multidimensional integration in stochastic mechanics[J]. International Journal for Numerical Methods in Engineering, 2004, 61(12): 1992-2019. [17] 韩增尧. 复杂航天器声振力学环境预示技术研究[D]. 北京:中国空间技术研究院,2000. [18] 徐孝诚,尹立中. 关于结构高频响应分析中有限元网格划分的细化标准[J]. 振动与冲击,2002,21(1):52-53. XU Xiaocheng, YIN Lizhong. On fining standard of fem meshing used in high frequency structure response analysis[J]. Journal of Vibration and Shock, 2002, 21(1): 52-53. [19] 漆文邦,郑超. 基于单元不同长宽比网格划分的有限元误差分析研究[J]. 中国农村水利水电,2010(2):108-110. QI Wenbang, ZHENG Chao. A study of sensitivity to mesh distortion of isoparameter elements[J]. China Rural Water and Hydropower, 2010(2): 108-110.2.3 多重Gauss-Hermite积分
2.4 误差分析

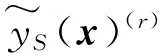
3 数值仿真
3.1 模型建立


3.2 网格单元划分

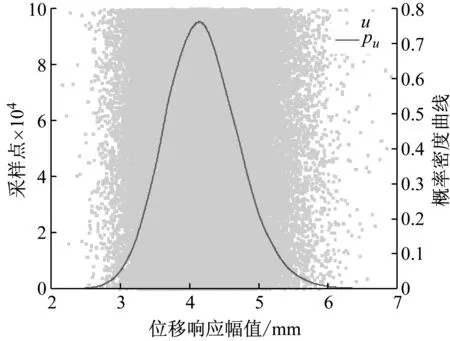
3.3 位移响应预测分析


3.4 变弹性随机边界条件的影响



4 结 论

