空间刚性梁轨道与姿态耦合动力学问题的辛分析

尹婷婷， 邓子辰,2， 蒋宪宏

(1. 西北工业大学 力学与土木建筑学院，西安 710072； 2. 大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116023)

梁的动力学问题是一个古老的力学问题，一直备受学术界关注。在过去的一个多世纪中，欧拉-伯努利梁模型和铁木辛柯梁模型相继被提出，并用于描述柔性梁的动力学问题，取得了一系列的创新性成果。以上两种经典梁理论所不同的是，欧拉-伯努利梁模型在描述梁的动力学问题时基于以下假设：梁只有弯曲变形,而梁对剪切变形完全刚性,即忽略了剪切变形和转动惯量；而铁木辛柯梁模型则考虑剪切变形与转动惯量。从模型的完备性方面看，铁木辛柯梁模型能够更好地描述柔性梁的动力学问题。

空间梁动力学问题相较于传统梁动力学问题[1]，具有以下特点：① 空间梁边界条件可以设定为两端自由边界，而经典梁模型通常包括简支、固支等情形；② 空间梁需要考虑大范围运动与姿态及结构振动间的耦合效应，而经典梁模型仅仅考虑结构振动问题；③ 空间梁由于所处工作环境复杂，因此所受载荷相对复杂。由于以上的特点，空间梁的动力学问题已经引起了力学界的广泛关注：Silva等[2-3]在考虑重力梯度影响的基础上，给出了空间柔性梁的建模方法和数值模拟结果，首开空间梁动力学问题的研究先河；Chen等[4]开展了关于空间柔性梁的几何非线性分析，得到了一些有意义的结果；Quadrelli等[5]基于多体动力学理论，采用混合变分方法研究了空间梁的动力学行为，其研究成果对于本文数值结果的分析具有一定的参考意义；刘锦阳等[6]基于连续介质理论，建立了大范围运动空间梁耦合动力学模型，并初步仿真分析了空间梁的耦合效应；Zhang等[7-8]采用欧拉-伯努利梁模型分析了空间刚柔耦合结构的动力学行为，将刚柔耦合动力学分析思想引入空间结构分析，具有广泛的应用前景；最近，Hu等考虑大跨度空间柔性阻尼梁的结构、姿态与轨道耦合问题，建立了动力学方程模型，并采用广义多辛分析方法[9-10]得到了空间柔性阻尼梁的阻尼效应及其平衡态条件，为本文的建模过程提供了理论依据。

在针对大跨度空间柔性阻尼梁的保结构分析过程中，由于构件跨度大，因此构件的柔性将不容忽视，也就是构件的柔性变形及振动不可忽略。不可否认，空间结构中大跨度的梁结构是比较常见的[11]，同时也应该意识到，空间结构中许多连接件的结构跨度比较小且相对刚度较大，这类构件在轨组装之前，如果依然采用已有文献[12]的建模和分析方法，虽然能使得动力学分析结果更为精确，但是将大大增加计算复杂度，无法为构件的实时轨道和姿态主动控制预留足够的时间，以致于无法及时完成组装过程。因此，在实际工程中，这类构件可以简化为刚性梁然后开展动力学行为分析，并忽略其阻尼效应。基于此，本文将针对空间刚性梁的平面运动与自身姿态之间的强耦合问题，采用辛数学方法[13]分析空间刚性梁的耦合动力学特性，为空间结构构件的主动控制设计提供参考。

1 空间刚性梁的耦合动力学模型

考虑一刚性梁的轨道与姿态耦合问题，如图1所示。假定刚性梁受地球中心引力场作用，只考虑其在平面轨道上做面内运功，忽略太阳光压、大气阻力、日月引力等摄动力的影响。假定该刚性梁运行在地球同步轨道上，建立地球赤道平面的惯性极坐标系：以地心O为坐标系的极点，极轴OX指向春分点，空间刚性梁的质心位置M可用极坐标表示为(r,θ)，r为质心M到地心O的距离，并称为极径，θ为极轴OX与OM之间的夹角，并称为极角。此外，以轴线OM与空间刚性梁之间的夹角α描述空间梁的姿态变化。

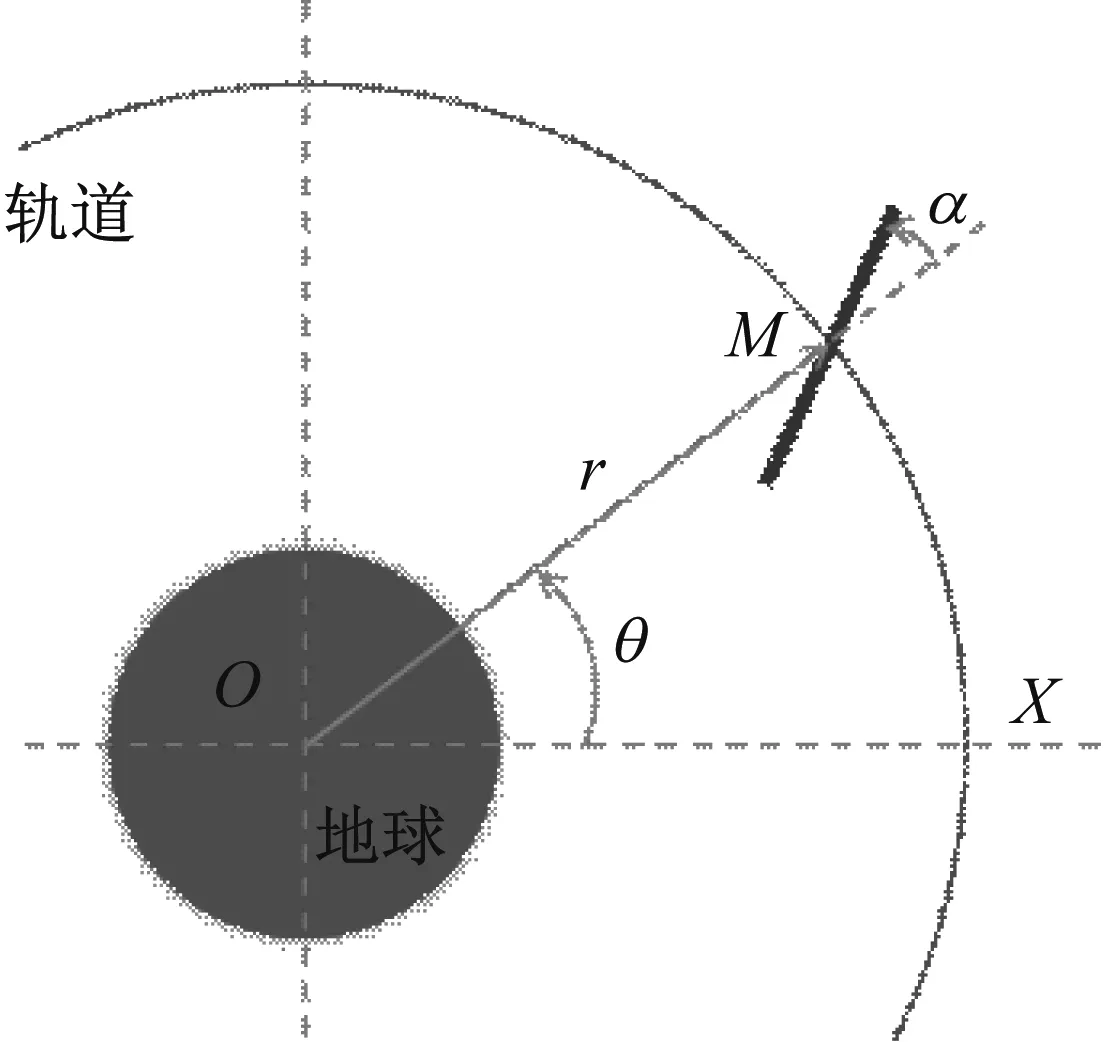
图1 空间刚性梁轨道与姿态耦合动力学模型

简化的空间刚性梁模型长度为l，线密度为ρ，其空间位形可用极坐标描述为

q=[q1q2q3]T=[rθα]T

三个广义坐标的物理意义分别为：r表示空间刚性梁模型在轨运行的轨道半径；θ表示空间刚性梁质心的轨道转角(即真近角)；α表示空间刚性梁模型的姿态角。

空间刚性梁模型系统的动能可以表示为

(1)

系统势能可以表示为[14]

(2)

式中：μ为地球引力常数，势能表达式中的第二项为引力梯度近似项，在梁的跨度不大的情况下，可以忽略其他引力梯度高阶项。

引入Lagrange函数

(3)

根据第二类Lagrange方程

(4)

可以推导得到空间刚性梁模型的动力学控制方程

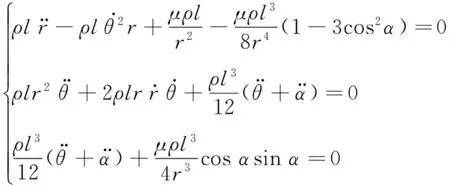
(5)

方程式(5)是一个高度非线性的二阶微分方程组，由于受到万有引力梯度的影响，空间刚性梁模型的轨道坐标和姿态坐标耦合在一起，这为空间刚性梁的动力学分析带来了极大的不便。

2 辛分析方法

上一节已提到，方程式(5)是一个强非线性系统，无法采用现有的理论得到其解析解，因此，空间刚性梁的轨道与姿态耦合动力学分析必须借助于合适的数值分析方法。由于空间结构构件的一个突出需求就是其在轨服役时间长，因此，所使用的数值分析方法需要具有长时间的数值稳定性，而保结构分析方法正好能够满足这一特殊的需求。

保结构分析方法起源于冯康院士提出的辛几何算法[15]，近年来已经发展推广至针对无限维动力学系统的(广义)多辛分析方法[16]，并逐渐形成了较为完整的理论体系。冯康院士在提出辛几何算法的初期，就已经开始尝试将辛几何算法应用于天体力学的研究，并对天体运动行为进行了长时间的预测，这为本文的研究工作奠定了理论基础。

(6)

龙格库塔方法由于其程序模块化程度高，稳定性好，备受计算数学家的青睐。然而，从保结构的观点看，龙格库塔方法并不能自动保辛，因此，Feng[17]通过添加人工约束，使得龙格库塔方法在某些特殊情形下满足保辛要求，从而发展成了辛龙格库塔方法。以下就从传统龙格库塔方法出发，简要介绍辛龙格库塔方法。s级的经典龙格库塔方法的一般格式为

(7)

Sanz-Serna等[18]已经证明式(7)是辛的，当且仅当其系数满足如下的条件

bibj-aijbi-ajibj=0

(8)

式中：i,j=1,2,…,s。

在式(8)中，当系数aij、bi取不同的值时，可以得到不同的辛龙格库塔格式。一种常用的2级4阶辛龙格库塔格式，其系数aij、bi取值为

(9)

采用2级4阶辛龙格库塔方法离散对偶方程式(6)，即可得到刚性梁轨道与姿态耦合动力学模型的辛龙格库塔格式。

3 数值实验

图2 轨道半径扰动量的演化情况

图3 真近角的演化情况

图4 姿态角的演化情况

从图2～图4中不难发现，当初始姿态角速度为零时，刚性梁的圆周运动与自身的转动之间没有发现显著的耦合效应，这是因为由于梁的尺寸很小，引力梯度的影响难以在数值结果中得到体现；当初始姿态角速度不为零时，刚性梁轨道与姿态之间的耦合效应比较明显，随着初始姿态角速度的增大，轨道半径扰动增大，刚性梁圆周运动周期缩短(表现为真近角增长速度的增大)，姿态角振动幅值略有减小(为了反映出振动幅值略有减小的趋势，在图4中将姿态角的模拟时间延长至2 160 h)。

以上模拟结果从一定程度上反映了刚性梁轨道与姿态之间的耦合效应，这些耦合效应还需要得到试验的进一步验证。然而，空间刚性梁的试验耗资巨大，因此，本文将从另一个角度对以上结果加以验证。我们注意到，式(5)是一个严格的保守动力学系统，而辛方法的最大优点就是能够长时间保持系统的整体能量，因此，在模拟过程中记录每一时间步的系统总能量

(10)

然后，得到每一时间步的总能量值与初始时刻能量值之间的相对误差，记为

以case 3情形为例，得到的每个时间点的总能量相对误差如图5(a)所示。为了与辛方法做对比，展现辛方法的保结构优势，本文同时采用传统四阶龙格库塔格式模拟空间刚性梁的空间运动与姿态演化，在模拟过程中记录总能量相对误差，所得到的能量相对误差如图5(b)所示。

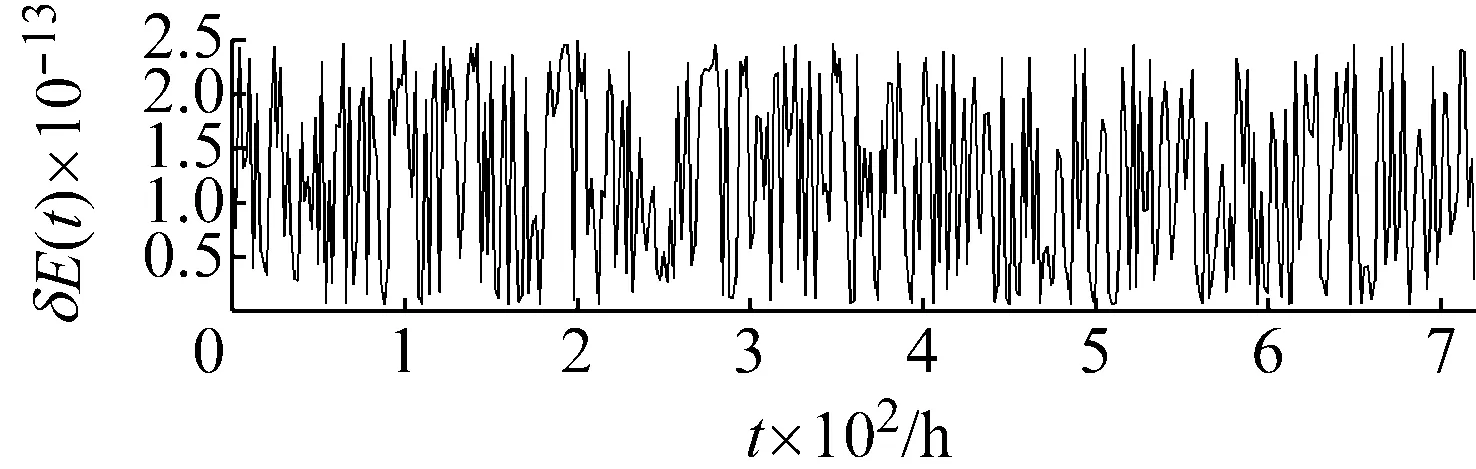
(a) 辛方法能量相对误差结果

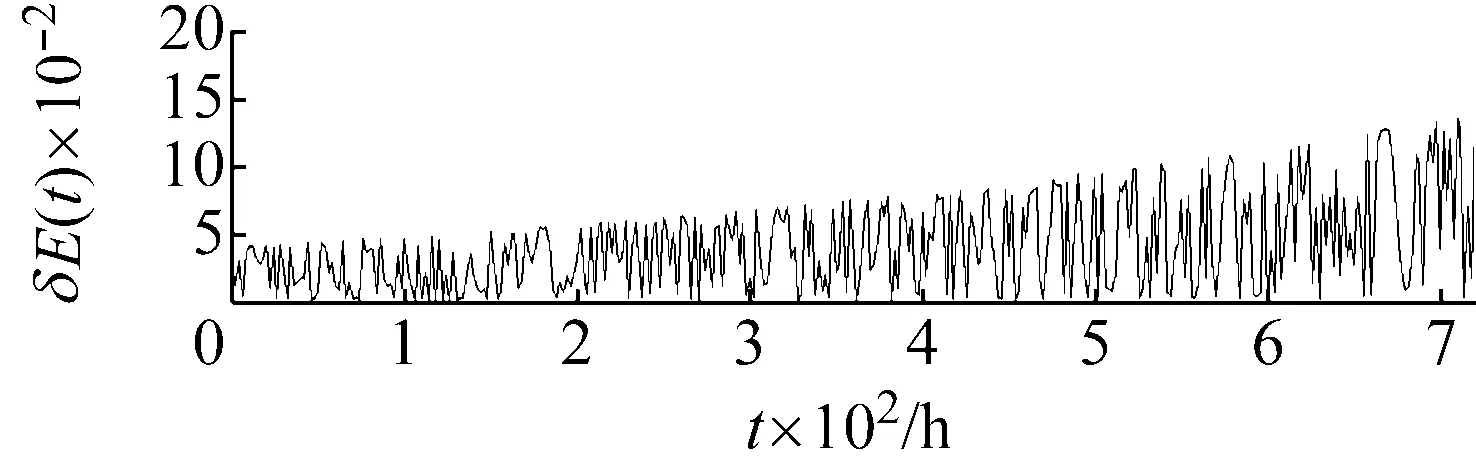
(b) 龙格库塔方法能量相对误差结果

从图5中可以看出，采用辛分析方法能够长时间保持系统总能量这一守恒量；而使用传统四阶龙格库塔格式得到的系统总能量相对误差的数量级远高于使用辛方法所得到的对应结果，并且随着模拟时间的延长，误差累积明显，当模拟时长至700 h后，累积的能量相对误差超过10%。以上结果间接地证明了相对于传统的龙格库塔方法，本文采用辛方法得到的刚性梁轨道与姿态耦合效应的数值结果是可信的。

4 结 论

近年来，空间柔性梁模型及数值分析方法引起了学术界的广泛关注，然而，空间柔性梁的动力学模型异常复杂，相应的数值分析方法效率不高，这难以满足结构主动控制的要求，为此，本文着眼于空间结构中某些大刚度小尺寸连接件，这些连接件在轨组装之前的动力学模型没有必要采用柔性梁模型进行动力学分析，本文将其简化为空间刚性梁，建立了其轨道与姿态相互耦合的动力学模型。针对建立的动力学模型，采用辛龙格库塔方法进行了刚性梁的耦合动力学分析，得到了如下结论：

(1) 当刚性梁的初始姿态角速度为零时，从数值结果中无法体现出姿态与轨道的耦合效应，其原因是，相对于轨道半径，刚性梁的尺寸极小，引力梯度的影响难以在本文数值结果中得到体现。这种情形下姿态与轨道耦合效应尚需要发展更为精确的数值方法加以分析。

(2) 随着刚性梁初始姿态角速度的增大，刚性梁的姿态与轨道耦合效应将愈发明显，耦合效应体现在：随着初始姿态角速度的增大，轨道半径扰动增大，真近角增长速度的增大，姿态角振动幅值略有减小。

以上结论的正确性从文中最后关于系统总能量相对误差的结果中得到间接证明，同时，数值方法的长时间稳定性也得到了相应的检验。

参 考 文 献

[1] 刘锦阳, 洪嘉振. 大范围运动空间梁的耦合动力学模型[J]. 上海交通大学学报, 2003, 37(4):532-534.

LIU Jinyang, HONG Jiazhen. Coupling dynamic modeling of the spatial beam undergoing large overall motions[J]. Jornal of Shanghai Jiao Tong University, 2003, 37(4):532-534.

[2] SILVA M R C, ZARETZKY C L. Nonlinear dynamics of a flexible beam in a central gravitational field—I. Equations of motion[J]. International Journal of Solids and Structures, 1993, 30(17):2287-2299.

[3] SILVA M R C, ZARETZKY C L. Nonlinear dynamics of a flexible beam in a central gravitational field—II. Nonlinear motions in circular orbit[J]. International Journal of Solids and Structures, 1993, 30(17):2301-2316.

[4] CHEN Z Q, AGAR T J A. Geometric nonlinear analysis of flexible spatial beam structures[J]. Computers & Structures, 1993, 49(6):1083-1094.

[5] QUADRELLI B, ATLURI S. Analysis of flexible multibody systems with spatial beams using mixed variational principles[J]. International Journal for Numerical Methods in Engineering, 1998, 42(6):1071-1090.

[6] 刘锦阳, 李彬, 洪嘉振. 作大范围空间运动柔性梁的刚-柔耦合动力学[J]. 力学学报, 2006, 38(2):276-282.

LIU Jinyang, LI Bin, HONG Jiazhen. Rigid-flexible coupling dynamics of a flexible beam with three-dimensional large overall motion[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(2):276-282.

[7] ZHANG Z G, QI Z H, WU Z G, et al. A spatial Euler-Bernoulli beam element for rigid-flexible coupling dynamic analysis of flexible structures[J]. Shock and Vibration, 2015(2): 1-15.

[8] 张志刚, 齐朝晖, 吴志刚, 等. 考虑变形耦合的几何非线性空间梁单元[J]. 计算力学学报, 2014, 31(5):603-608.

ZHANG Zhigang, QI Zhaohui, WU Zhigang, et al. A geometrical nonlinear space beam element with considering deformation coupling[J]. Chinese Journal of Computational Mechanics, 2014, 31(5):603-608.

[9] HU W P, DENG Z C, HAN S M, et al. Generalized multi-symplectic integrators for a class of Hamiltonian nonlinear wave PDEs[J]. Journal of Computational Physics, 2013, 235(4):394-406.

[10] 胡伟鹏, 邓子辰, 吴子燕, 等. 桥梁在移动荷载作用下动力学响应的广义多辛算法[J]. 振动与冲击, 2008, 27(4):66-69.

HU Weipeng, DENG Zichen, WU Ziyan, et al. Generalized multi-symplectic method for bridges subjected to moving loads[J]. Journal of Vibration and Shock, 2008, 27(4):66-69.

[11] 徐圣, 刘锦阳, 余征跃. 几何非线性空间梁的动力学建模与实验研究[J]. 振动与冲击, 2014, 33(21):108-113.

XU Sheng, LIU Jinyang, YU Zhengyue. Dynamic modeling and tests for a geometric nonlinear spatial beam[J]. Journal of Vibration and Shock, 2014, 33(21):108-113.

[12] HU W P, LI Q J, JIANG X H, et al. Coupling dynamic behaviors of spatial flexible beam with weak damping[J]. International Journal for Numerical Methods in Engineering, 2017, 111: 660-675.

[13] 刘铁权，邓子辰， 周加喜. 基于辛数学方法的一维声子晶体禁带计算[J]. 振动与冲击, 2010, 29(12):102-105.

LIU Tiequan, DENG Zichen, ZHOU Jiaxi. Symplectic method for calculation of band gap of one-dimensional phononic crystals[J]. Journal of Vibration and Shock, 2010, 29(12):102-105.

[14] 邓子辰, 曹珊珊, 李庆军, 等. 基于辛 Runge-Kutta 方法的太阳帆塔动力学特性研究[J]. 中国科学(技术科学), 2016, 46: 1242-1253.

DENG Zichen, CAO Shanshan, LI Qingjun, et al. Dynamic behavior of sail tower SPS based on the symplectic Runge-Kutta method[J]. Scientia Sinica(Technologica), 2016, 46:1242-1253.

[15] FENG K. On difference schemes and symplectic geometry[C]//Proceeding of the 1984 Beijing Symposium on Differential Geometry and Differential Equations. Beijing: Science Press, 1984: 42-58.

[16] BRIDGES T J. Multi-symplectic structures and wave propagation[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1997, 121(1):147-190.

[17] FENG K. Difference-schemes for Hamiltonian-Formalism and symplectic-geometry[J]. Journal of Computational Mathematics, 1986, 4(3):279-289.

[18] SANZ-SERNA J M. Runge-Kutta schemes for Hamiltonian systems[J]. BIT Numerical Mathematics, 1988, 28(4):877-883.