Strongly Ding projective modules with respect to a semidualizing module
(1.School of Mathematics and Physics,Anhui University of Technology,Maanshan 243032,P.R.China;2.Institute of Mathematics,School of Mathematics Sciences,Nanjing Normal University,Nanjing 210023,P.R.China)
§1. Introduction
Throughout,unless otherwise indicated,all rings are commutative rings with identity and all modules are unitary modules.Auslander and Bridger[1]introduced the G-dimension for finitely generated modules.Enochs and Jenda de fined and studied the Gorenstein projective,Gorenstein injective[8]and Gorenstein flat modules[10]and developed Gorenstein homological algebra[9]on modules over a ring R.Various generalizations of these modules are given over speci fic rings(see,e.g.,[12-14,17-18,23,27,31-32]).As special cases of Gorenstein projective and Gorenstein injective modules,strongly Gorenstein flat and Gorenstein FP-injective modules were studied in[6-7],and later in[11]under di ff erent names—the Ding projective and Ding injective modules.It was shown in[6]that the class of Ding projective modules over coherent rings are indeed stronger than Gorenstein flat modules.This class of modules can gives some new interesting characterizations of rings.For example,it was proved in[6,Proposition 2.15]that a ring R is right perfect if and only if every flat right R-module is Ding projective.
Recently,Ding projective dimensions and strongly Ding projective modules were further investigated in[30].More generally,Ding projective modules and Ding projective dimensions with respect to a semidualizing module were studied in[29]and[31].In this paper,we study the concept of strongly Ding projective modules with respect to a semidualizing module.The properties of strongly DC- flat modules under change of rings are also investigated.The paper is organized as follows.In section 2,we give some notions and de finitions which we need in the later sections.Section 3 is a study of strongly Ding projective modules with respect to a semidualizing module.The concept of strongly DC-projective modules is introduced and some characterizations of this class of modules are given.Strongly Ding projective modules are a particular case of strongly DC-projective modules when C=R.In Section 4,we study the properties of strongly Ding flat modules with respect to a semidualizing module.It is proved that if M is a strongly DC- flat module,then M+is strongly DC-injective.Some results on strongly Ding flat modules are obtained as corollaries of these results.
§2. Preliminaries
An R-module M is called FP-injective[21]in casefor every finite presented R-module P.A degreewise finite projective resolution of an R-module M is a projective resolution P of M such that each Piin P is finitely generated projective.A class of modules X is projectively resolving if it is closed under extensions,kernels of surjections and it contains all projective modules[17].
De finition 2.1An R-module C is semidualizing if the following conditions are satis fied:
(1)C admits a degreewise finite projective resolution,
(2)The natural homothety morphism R→HomR(C,C)is an isomorphism,
(3)
Two examples of semidualizing modules are the free module of rank 1,and the dualizing(canonical)module over a Cohen-Macaulay local ring,when it exists.
De finition 2.2Let C be a semidualizing R-module.Set

Modules in PC(R),FC(R),IC(R)and FIC(R)are called C-projective,C- flat,C-injective and C-FP-injective,respectively.
Clearly,if C=R,then PR(R),FR(R),IR(R)and FIR(R)are just the classes of ordinary projective,flat,injective and FP-injective R-modules,respectively,which are denoted by F(R),P(R),I(R)and FI(R),respectively,for simplicity.By[19,Proposition 5.1],PC(R)is closed under direct sums and direct summands,and IC(R)is closed under direct products and direct summands.Moreover,the classes PC(R)and FC(R)are projectively resolving,and the class IC(R)is injectively resolving by[19,Corollary 6.4].
De finition 2.3[6−7,11]An R-module M is called Ding projective if there exists an exact sequence of projective R-modules

withsuch that HomR(P,F(R))is exact.Ding injective module is dually de fined.An R-module N is called Ding flat if there exists an exact sequence of flat R-modules
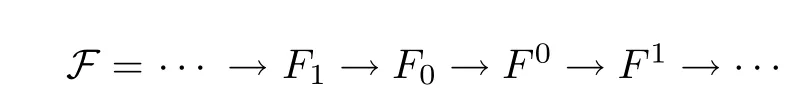
withsuch thatis exact.
It is easy to see that Ding projective(resp.,Ding injective)modules are Gorenstein projective(resp.,Gorenstein injective).But Gorenstein injective modules over a Noetherian ring is Ding injective.
De finition 2.4Let X be a class of R-modules and M an R-module.Then an X-resolution of M is a complex of R-modules in X of the form

such thatandfor all n ≥ 1.Moreover,the exact sequence

is called the augmented X-resolution of M associated to
Given a class X of R-modules and a complex Y,we say Y is HomR(X,−)-exact if the complex HomR(X,Y)is exact for each X ∈ X.Dually,the complex Y is HomR(−,X)-exact if HomR(Y,X)is exact for each X ∈X,and Y isX-exact ifis exact for each X∈X.The X-projective dimension of M is de fined as

An X-resolutionof M is proper if the augmented resolutionis HomR(X,−)-exact.The(proper)X-coresolution and X-injective dimensions can be de fined dually.And the X-injective dimension of M is denoted by X-idR(M).
Note 2.5Let C be a semidualizing R-module.We use the following abbreviations
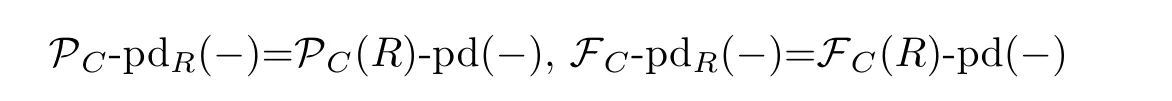
Over a commutative Noetherian ring R,Foxby[14]studied two subcategories of the category of R-modules relative to a(semi)dualizing module C,which are the Auslander class AC(R)and Bass class BC(R).In the non-Noetherian setting,these de finitions are taken from[19,26].
De finition 2.6The Auslander class AC(R)with respect to C consists of all R-modules M satisfying:and the natural map µM:M →is an isomorphism.
The Bass class of R with respect to C,denoted BC(R),consists of all R-modules N satisfying:and the natural evaluation map νN:is an isomorphism.
§3. Strongly DC-projective Modules
In this section,we introduce and study strongly Ding projective modules with respect to a semidualizing module.
We begin with the following
De finition 3.1An R-module M is said to be n-strongly Ding projective with respect to C(or simply n-strongly DC-projective),if there exists an exact sequence

such that P is HomR(−,FC(R))-exact,where each Piis projective for all 1≤ i≤ n.
If C=R,then we call a n-strongly DC-projective module a n-strongly Ding projective module.It is easy to see that every n-strongly Ding projective module is n-strongly Gorenstein projective[2].We denote by n-SDPC(R)the subcategory of n-strongly DC-projective R-modules.The subcategory of n-strongly Ding projective modules is denoted by n-SDP(R).
Remark 3.2
(1)We call a 1-strongly DC-projective module a strongly DC-projective module,for simplicity.Clearly,1-strongly DR-projective modules are precisely the class of strongly Ding projective modules.Every strongly Ding projective module is strongly Gorenstein projective[3].
(2)Let M be an n-strongly DC-projective module andwithIt is easy to see that each Kiis n-strongly DC-projective for all i.Similarly,we can easily check that eachis n-strongly DC-projective for all 2≤i≤n.
Recall that an R-module M is Ding projective with respect to C(or simply DC-projective),if there exists an exact sequence of C-projective R-modules

withsuch that the sequence is HomR(−,FC(R))-exact.
The next lemma is a corollary of[29,Theorem 2.7],which shows that the class of DC-projective modules coincides with the DC-projective modules de fined in[29].
Lemma 3.3An R-module M is DC-projective if and only if there exists a HomR(−,FC(R))-exact exact sequence

such that alland
The following result gives some equivalent characterizations of n-strongly DC-projective modules.
Theorem 3.4Let M be an R-module.Then the following are equivalent
(1)M is an n-strongly DC-projective module.
(2)There exists an exact sequence

with each Piprojective such that
(3)There exists an exact sequence

with each Piprojective such that the sequence is HomR(−,F)-exact for every module F with
(4)There exists an exact sequencewhere each Piis projective,and there exists a positive integer k such that
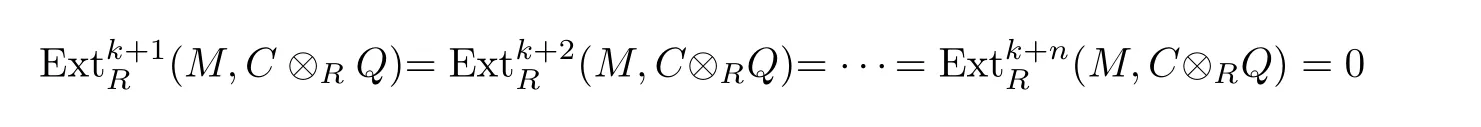
for every
(5)There exists an exact sequencewhere each Piis projective,and there exists a positive integer k such that

for every module N with
Proofandare obvious by De finition 3.1.
Let M be an n-strongly DC-projective module.Then there exists an exact sequence
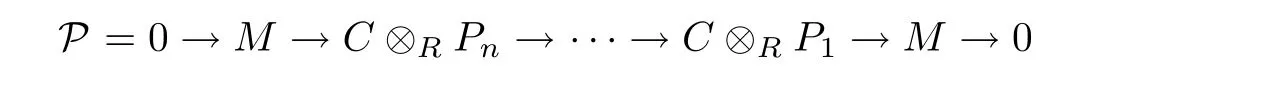
such that P is HomR(−,FC(R))-exact,where each Piis projective.Let F be a module and m≥1 a positive integer such thatThen there is an exact sequence 0→K→V→F→0 with V∈FC(R)andSince every n-strongly DC-projective module is DC-projective by Proposition 3.6(3),it follows thatby Lemma 3.3 and[29,Proposition 1.5].
Moreover,sinceby[19,Corollary 6.1]andby[15,Corollary 3.2(2)],we havefor 1≤i≤n by dimension shifting.This implies that the sequence of complexes

is exact.Moreover,since the complexes HomR(P,K)and HomR(P,V)are exact by inductive hypothesis,we conclude that the complex HomR(P,F)is exact.
(2)⇔(4).Assume that M is n-strongly DC-projective,then there exists an exact sequence

with each Piprojective such thatSinceby[19,Corollary 6.1]and[15,Corollary 3.2(2)]by dimension shifting,we have the isomorphism

for all k≥1,where Q is a flat R-module.Therefore,if the n successive terms ofis zero,then we havewith Q an flat R-module and k≥1.
The proof is similar to that of
Corollary 3.5[30,Theorem3.2]Let M be an R-module.Then the following are equivalent
(1)M is strongly Ding projective.
(2)There exists an exact sequence 0→M→P→M→0 with P projective such that
(3)There exists an exact sequence 0→M→P→M→0 with P projective such that the short sequence 0→HomR(M,F)→HomR(P,F)→HomR(M,F)→0 is exact for every flat R-module F.
(4)There exists an exact sequence 0→M→P→M→0 with P projective such that the short sequence 0→HomR(M,F)→HomR(P,F)→HomR(M,F)→0 is exact for every R-module F with finite flat dimension.
The next proposition reveals the relations between strongly DC-projective module,n-strongly DC-projective modules and DC-projective modules.
Proposition 3.6Let n and m be two positive integers.Then the following statements hold
(1)Every strongly DC-projective module is n-strongly DC-projective.
(2)If m=kn,then every n-strongly DC-projective module is m-strongly DC-projective.
(3)Every n-strongly DC-projective module is DC-projective.
(4)For any n≥1,the class n-SDPC(R)is closed under direct sums.
(5)If M is n-strongly DC-projective andwith 1 ≤ i≤ nthenis strongly DC-projective.
Propostition 3.6Let R be a coherent ring.Then an R-module M is DC-projective if and only if it is a direct summand of a strongly DC-projective module.
ProofThe proof is similar to that of[3,Theorem 2.7].
Lemma 3.8Let m and n be two positive integers.Then we have
(1)If m=kn,thenT
(2)If m=kn+i with k a positive integer and 0 Proof(1)follows directly from Proposition 3.6. (2)The proof is a modi fication of that of[28,Proposition 3.4].Note thatTby Proposition 3.6.LetTThen there exists an exact sequencesuch that P is HomR(−,FC(R))-exact,where each Piis projective.Let Hi=for 2≤ i≤ m.Sinceand PC(R)is closed under direct sums,there existandwithandprojective such that Sinceand PC(R)is closed under extensions by[19,Proposition 5.2],we have.Consider the following pullback diagram Becauseand PC(R)is projectively resolving by[19,Corollary 6.4],we have Y∈PC(R).Now combining the sequence P and the first row in the above diagram,we obtain the following exact sequence: which is HomR(−,FC(R))-exact.This implies that M is i-strongly DC-projective.Therefore,T Proposition 3.9Twhere(m,n)is the greatest common divisor of m and n. ProofThe implicationis obvious by Proposition 3.6(2).It suffices to prove the converse inclusion.If m=nq0+r0with 0 Theorem 3.10Let M be an R-module and n≥1.Then the following statements are equivalent (1)M is an n-strongly DC-projective module. Prooffollows from Proposition 3.6(5).andare trivial by Proposition 3.6.It suffices to proveSuppose that there exists an exact sequence Recall that an R-module M is n-strongly Gorenstein flat[28],if there exists an exact sequence 0→ M → Fn→ ···→ F1→ M → 0 with each Fiflat such that− leaves the sequence exact whenever I is an injective R-module. More generally,we give the following De finition 4.1An R-module M is said to be an n-strongly DC- flat module,if there exists an exact sequence with each Fiflat for any 1≤i≤n,such that the sequence is−exact. We denote by n-SDFC(R)the subcategory of n-strongly DC- flat R-modules relative to the semidualizing module C.Recall that an R-module M is called DC- flat,if there exists an exact sequence of C- flat R-modules withsuch that the sequence is− exact,where all Fi,Fiare flat R-modules. Remark 4.2(1)If C=R,it is easy to see that DC- flat modules are just the class of Ding flat modules,and n-strongly DC- flat modules are precisely the class of n-strong Ding flat modules.Clearly,every n-strongly DC- flat module is DC- flat and every n-strong Ding flat module is Ding flat. (2)We call a 1-strongly DC- flat module a strongly DC- flat module,for simplicity.In particular,a 1-strongly DR- flat module is called to be a strongly Ding flat module.Clearly,every strongly DC- flat module is n-strongly DC- flat. De finition 4.3An R-module M is said to be n-strongly DC-injective,if there exists an exact sequence with each Iiinjective for any 1≤ i≤ n such that the sequence is HomR(FIC(R),−)− exact. It was shown in[28,Proposition 4.9]that if M is an n-strongly Gorenstein flat module,the M+is n-strongly Gorenstein injective.Similarly,we have the following Proposition 4.4If M is an n-strongly DC- flat module,then M+is n-strongly DC-injective. ProofSuppose that M is n-strongly DC- flat.Then there exists an exact sequence with each Fiflat such that F isexact,and thusfor every FP-injective R-module I.Therefore,we have the following exact sequence with eachinjective.Moreover,we have the isomorphism for any i≥1 by[4,Chapter VI,Proposition 5.1],whereThis implies that the exact sequence F+is− exact,and thus M+is n-strongly DC-injective. Lemma 4.4Let R be a coherent ring.Then an R-module M is C-FP-injective if and only if its character module M+is C- flat. ProofAssume that M is C-FP-injective.Then we can write M as HomR(C,E)for some FP-injective R-module E.Since C has a degreewise finite projective resolution and Q/Z is injective,we have the following by the Hom-evaluation isomorphism.Moreover,E+is a flat module by[5,Theorem 1]since R is coherent,and hence M+is C- flat.Conversely,if M+is C- flat then M+∈BC(R)andis a flat R-module by[19,Lemma 5.1(a)].This implies thatis a FP-injective module by[5,Theorem 1].Since M+∈BC(R),we have the isomorphisms Here the second isomorphism follows from the adjoint isomorphism and the third one is the Hom-evaluation isomorphism since C has a degreewise finite projective resolution and Q/Z is injective.This implies thatis C-FP-injective. The next proposition shows that n-strongly DC-projective modules over coherent rings are indeed stronger than n-strongly DC- flat modules. Proposition 4.6Let R be a coherent ring.Then every n-strongly DC-projective R-module is n-strongly DC- flat. ProofSuppose that M is an n-strongly DC-projective R-module.Then there exists an exact sequence of R-modules such that P is HomR(−,FC(R))-exact,where each Piis projective.For any C-FP-injective R-module HomR(C,I),we note that HomR(C,I)+is C- flat by Lemma 4.5.Now applying the functor HomR¡−,HomR(C,I)+¢to the exact sequence P,we get the exact sequence which gives the exactness of the sequence This implies that the following sequence is exact.Therefore,M is an n-strongly DC- flat module. Corollary 4.7Let R be a coherent ring.Then every n-strongly Ding projective module is n-strongly Gorenstein flat. Let R and S be two commutative rings.Recall that a ring homomorphism ϕ :R → S is a flat ring homomorphism if S is a flat R-module. Lemma 4.8[25,Theorem3.4.1]Let C be a semidualizing R-module and let ϕ :R → S be a ring homomorphism.Then S∈AC(R)if and only ifis a semidualizing S-module withfor all i≥1. Lemma 4.9Let ϕ :R → S be a flat ring homomorphism.If M is FP-injective as an S-module,then M is FP-injective as an R-module. ProofLet N be a finitely presented R-module.Then there is an exact sequence 0→K→P→N→0 of R-modules with K finitely generated and P finitely presented projective.Since ϕ:R→S is a flat ring homomorphism,we have the following exact sequence of S-modules It is clear that K⊗RS is finitely generated andis finitely generated projective.This implies that N⊗RS is finitely presented,and thussince M is FP-injective as an S-module.Therefore,we haveby[20,Theorem 11.65].It follows that M is an FP-injective R-module,as desired. Next we investigate the property of n-strongly DC- flat modules under change of rings. Proposition 4.10Let ϕ:R→S be a flat ring homomorphism.Ifthen ProofAssume that M∈n-SDFC(R).Then there exists an exact sequence with each Fiflat as R-module such that F isexact.Therefore,we havefor every FP-injective R-module I.Since S is a flat R-module,the complex is exact,and thus the complex is exact.It is easy to see that everyis flat as S-module for each i.Since S∈AC(R),is a semidualizing S-module by Lemma 4.8.It suffices to show that the complexis exact for every FP-injective S-module E.In fact,we have sinceand E is an FP-injective S-module,it follows that HomS(S,E)is an FP-injective R-module by Lemma 4.9.Now the result follows from the above isomorphism,and hence Corollary 4.11If ϕ :R → S is a flat ring homomorphism,then Proposition 4.12Let S be a multiplicatively closed set of a ring R.If M is n-strongly DC- flat,then S−1M is n-strongly DC- flat. ProofAssume that M is n-strongly DC- flat.Then there exists an exact sequence such that− exact,where each Fiis flat.Since S−1R is flat as an R-module,the following sequence is exact.For each i,we have the isomorphismsTherefore,we have the exact sequence Now it suffices to prove that the sequence− exact.In fact,for every HomR(C,E)∈FIC(R),we have the isomorphisms which implies that S−1F is FIC(R)⊗R− exact.Therefore,S−1M is n-strongly DC- flat. Corollary 4.13Let S be a multiplicatively closed set of a ring R.Then (1)If M is n-strongly Ding flat,then S−1M is n-strongly Ding flat, (2)If M is strongly Ding flat,then S−1M is strongly Ding flat, (3)If M is strongly DC- flat,then S−1M is DC- flat. Acknowledgments The author wishes to express his sincere thanks to the referee for the helpful comments and suggestions. [1]AUSLANDER M,BRIDGER M.Stable module theory[M].Mem.Amer.Math.Soc.,Vol.94,Amer.Math.Soc.,Providence,RI,1969. [2]BENNIS D,MAHDOU N.A generalization of strongly Gorenstein projective modules[J].J.Algebra Appl.,2009,8(2):219-227. [3]BENNIS D,MAHDOU N.Strongly Gorenstein projective,injective and flat modules[J].J.Algebra Appl.,2007,210:437-445. [4]CARTAN H,EILENBER S.Homological algebra[M].Princeton University Press,1956. [5]CHEATHAM T J,STONE D R.Flat and projective character modules[J].Proc.Amer.Math.Soc.,1981,81:175-177. [6]DING Nan-qin,LI Yuan-lin,MAO Li-xin.Strongly Gorenstein flat modules[J].J.Aust.Math.Soc.,2009,86(3):323-338. [7]DING Nan-qin,MAO Li-xin.Goresntein FP-injective and Gorenstein flat modules[J].J.Algebra Appl.,2008,7(4):491-506. [8]ENOCHS E E,JENDA O M G.Gorenstein injective and projective modules[J].Math.Z.,1995,220:611-633. [9]ENOCHS E E,JENDA O M G.Relative homological algebra[M].Walter de Gruyter,Berlin,2000. [10]ENOCHS E E,JENDA O M G,TORRECILLAS B.Gorenstein flat modules[J].Nanjing Daxue Xuebao(Shuxue Bannian Kan),1993,10:1-9. [11]GILLESPIE J.Model structures on modules over Ding-Chen rings[J].Homology,Homotopy Appl.,2010,12(1):61-73. [12]CHRISTENSEN L W.Gorenstein dimensions,Springer,Berlin,2000. [13]CHRISTENSEN L W,FRANKILDA,HOLM H.On Gorenstein projective,injective and flat dimensions-A functorial description with applications[J].J.Algebra,2006,302:231-279. [14]FOXBY H B.Gorenstein modules and related modules[J].Math.Scand.,1972,31:267-284. [15]GENG Yu-xian,DING Nan-qin.W-Gorenstein modules[J.J.Algebra,2011,325:132-146. [16]GOLOD E S.G-dimension and generalized perfect ideas[J].Algebraic geometry and its applications,Trudy Mat.Inst.Steklov,1984,165:62-66(in Russian). [17]HOLM H.Gorenstein homological dimension[J].J.Pure Appl.Algebra,2004,189(1-3):167-193. [18]HOLM H,JORGENSEN P.Semi-dualizing modules and related Gorenstein homological dimension[J].J.Pure Appl.Algebra,2006,205(2):423-445. [19]HOLM H,WHITE D.Foxby equivalence over associative rings[J].J.Math.Kyoto Univ.,2007,47(4):781-808. [20]ROTMAN J J.An introduction to homological algebra[M].Academic Press,New York,1979. [21]STENRSTRÖM B.Coherent rings and FP-injective modules[J].J.London Math.Soc.,1970,2:323-329. [22]VASCONCELOS W V.Divisor theory in module categories[M].North-Holland Publishing Co.,Amsterdam,1974. [23]WAGSTAFF S S,SHARIF T,WHITE D.Tate cohomology with respect to semidualizing modules[J].J.Algebra,2010,324:2336-2368. [24]WAGSTAFF S S,SHARIF T,WHITE D.Stability of Gorenstein categories[J].J.London Math.Soc.,2008,77(2):481-502. [25]WAGSTAFF S S.Semidualizing modules,http://www.ndsu.edu/pubweb/∼ssatherw/. [26]WHITE D.Gorenstein homological dimension with respect to a semidualizing module[J].J.Commut.Algebra,2010,2(1):111-137. [27]YANG Xiao-yan.n-strongly Gorenstein Projective and Injective and Flat Modules[J].Chin.Quart.J.of Math.,2014,29(4):553-564. [28]ZHAO Guo-qiang,HUANG Zhao-yong.n-strongly Gorenstein projective,injective and flat modules[J].Comm.Algebra,2011,39:3044-3062. [29]ZHANG Chun-xia,WANG Li-ming,LIU Zhong-kui.Ding projective modules with respect to a semidualizing module[J].Bull.Korean Math.Soc.,2014,51(2):339-356. [30]ZHANG Chun-xia,WANG Li-ming.Strongly Gorenstein flat dimensions[J].J.Math.Res.Exposition,2011,31(6):977-988. [31]ZHAO Liang,ZHOU Yi-qiang.DC-projective dimensions,Foxby equivalence and SDC-projective modules[J].J.Algebra Appl.,2016,15(6):1650111(23 pages). [32]ZHAO Liang,WEI Jia-qun,HU Jiang-sheng.Weak Gorenstein cotorsion modules.Algebra Colloq.,to appear.

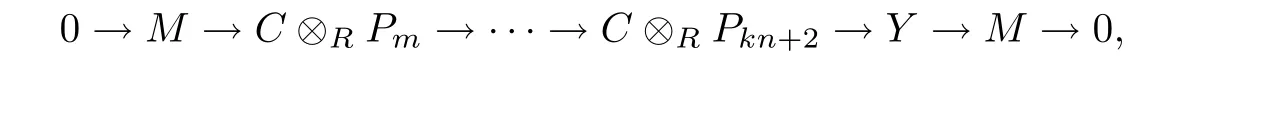
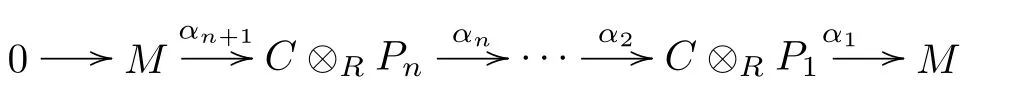




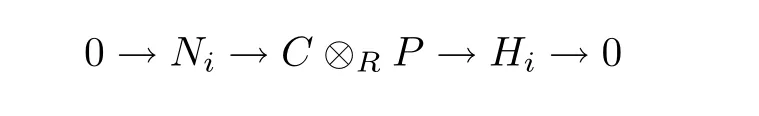
§4. Strongly DC- flat Modules




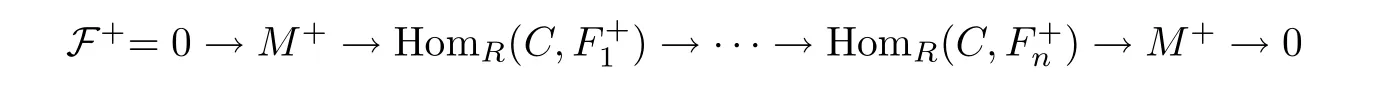





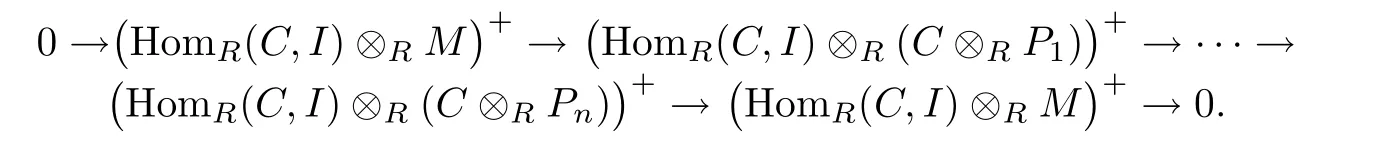
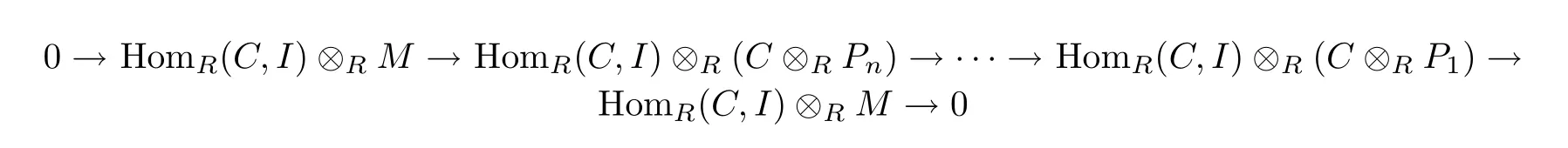
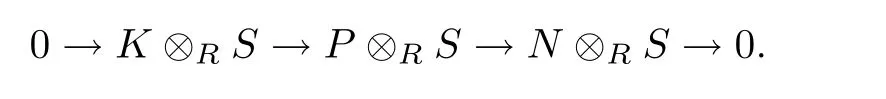



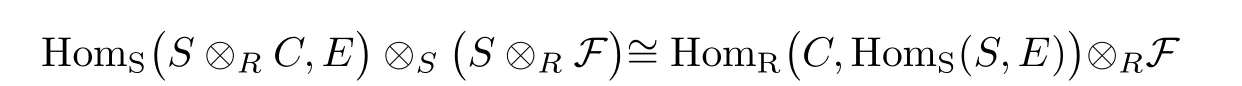

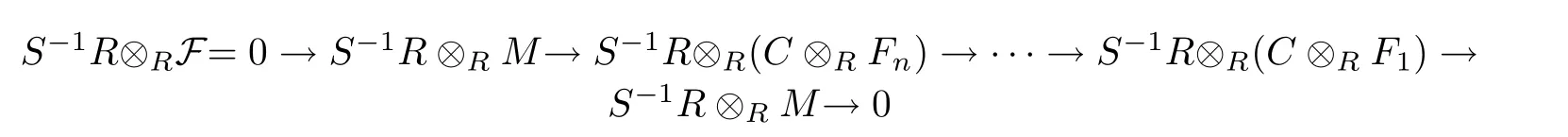


 Chinese Quarterly Journal of Mathematics2018年1期
Chinese Quarterly Journal of Mathematics2018年1期
