Strongly α-Reflexive Rings Relative to a Monoid
PENG Zhai-ming,GU Qin-qin,ZHANG Rui-rui
(1.1.School of Economic&Management,NanJing University of Science&Technology,Nanjing;2.School of Mathematics&Physics,Anhui University of Technology,Maanshan)
Abstract:For a monoid M and an endomorphism α of a ring R,we introduce the notion of strongly M-α-reflexive rings and study its properties.For an u.p.-monoid M and a right Ore ring R with its classical right quotient ring Q,we prove that R is strongly M-α-reflexive if and only if Q is strongly M-α-reflexive,where R is α-rigid,α is an epimorphism of R.The relationship between some special subrings of upper triangular matrix rings and strongly M-α-reflexive rings is also investigated.Several known results similar to strongly M-α-reversible rings are obtained.
Key words:Unique product monoid;α-reflexive ring;strongly M-α-reflexive ring;strictly totally ordered monoid
§1. Introduction
Throughout this paper,R denotes an associative ring with identity,α denotes a non-zero and non-identity endomorphism,unless specified otherwise.For a ring R,the polynomial ring with an indeterminate x over R is denoted by R[x]and the n by n full matrix ring over R is denoted by Mn(R).Also,for a monoid M,e stands for the identity of M,R[M]denotes the monoid ring over R.For a ring R with an endomorphism α,an endomorphism of Mn(R)induced by(aij)→(α(aij))is denoted by¯α.
In 1981,Mason[1] first studied the reflexive property of rings.A right ideal I is reflexive if xRy⊆I implies yRx⊆I for x,y∈R.R is called reflexive if(0)is a reflexive ideal(i.e.,aRb=(0)implies bRa=(0)for a,b∈R).Later,the properties of reflexive rings and related concepts were studied in[2].According to Hashemi and Moussavi[3],an endomorphism α of a ring R is called rigid if aα(a)=0 implies a=0 for all a ∈ R.A ring R is α-rigid if there exists a rigid endomorphism α of R.Also,a ring R is α-compatible if for each a,b ∈ R,ab=0 if and only if aα(b)=0.By[3,Lemma 2.2],a ring R is α-rigid if and only if R is α-compatible and reduced(i.e.,rings with no nonzero nilpotent elements).A ring R is called semicommutative if whenever ab=0 implies aRb=0.Reduced rings are semicommutative,but the converse is not true.As mentioned in[4],Zhao and Zhu studied a generalization of a reflexive ring and that of an α-rigid ring,which is called an α-reflexive ring,whenever aRb=0 implies bRα(a)=0 with a reflexive endomorphism α of R.Also in[5],Kwak,Lee and Yun called it a right α-skew reflexive ring.In 1997,Rege and Chhawchharia[6]introduced the notion of an Armendariz ring.They defined a ring R to be an Armendariz ring if whenever polynomials f(x)=a0+a1x+ ···+amxm,g(x)=b0+b1x+ ···+bnxn∈ R[x]satisfy f(x)g(x)=0,then aibj=0 for each i,j.Liu[7]called a ring R an M-Armendariz ring(an Armendariz ring relative to a monoid M),if whenever α =a1g1+a2g2+···+angn,β =b1h1+b2h2+···+bmgm∈ R[M]satisfy αβ =0,then aibj=0,for all i,j.In 2014,Elshokry,Ali and Liu[8]introduced the notion of 3-M-Armendariz rings,which is a generalization of an M-Armendariz ring,where M is a monoid.A ring R is called 3-M-Armendariz if whenever elements α =a1g1+···+angn,β =b1h1+ ···+bmhm, γ =c1l1+ ···+crlr∈ R[M],satisfy αβγ =0,then aibjck=0 for each i,j,k.As mentioned in[9],Singh,Juyal and Khan studied a generalization of a strongly reversible ring,which is called strongly M-reversible,whenever αβ =0 implies βα =0 with α,β ∈ R[M].Later,Ali,Elshokry and Liu[10]presented the concept of a strongly M-αreversible ring.For an endomorphism α of a ring R, α is called strongly right(respectively,left)reversible relative to M if whenever ϕ,ψ ∈ R[M]with ϕψ =0,then ψα(ϕ)=0(resp.,α(ψ)ϕ =0).A ring R is called strongly right(resp.,left)M-α-reversible if there exists a strongly right(respectively,left)reversible endomorphism α of R relative to M.A ring is strongly M-α-reversible if it is both strongly right and left M-α-reversible.In[11],a ring R is called strongly M-reflexive whenever α,β ∈ R[M]with αR[M]β =0,then βR[M]α =0.The extensions of reflexive rings,strongly reflexive rings,Armendariz rings and reversible rings have been discussed in a number of publications(see,for example,[7],[11],[12]).
Motivated by the above facts,we introduce the concept of a strongly M-α-reflexive ring for an endomorphism α of a ring R and a moniod M,as a generalization of an α-reflexive ring and that of a strongly M-reflexive ring.We study basic examples and properties of strongly M-α-reflexive rings.For a monoid M and a right Ore ring R with Q its classical right quotient ring,we prove that if R is α-rigid with epimorphism α,then R is strongly M-α-reflexive if and only if Q is strongly M-α-reflexive.It is shown that if R is a reduced α-reflexive ring,M is a u.p.-monoid,then T(R,R)is strongly M-¯α-reflexive.At last,we prove that some special subrings of upper triangular matrix rings over a reduced ring are strongly M-α-reflexive under some additional conditions,where M is a strictly totally ordered monoid.
§2. Strongly M-α-reflexive Rings
In this section,we introduce the notion of a strongly M-α-reflexive ring and consider its properties and basic extensions.Some examples related to strongly M-α-reflexive rings are given.
Let α be an endomorphism of a ring R.For ϕ =a1g1+ ···+angn∈ R[M],we denote α(a1)g1+ ···+ α(an)gnas α(ϕ).We start with the following definition.
Definition 2.1 An endomorphism α of a ring R is called strongly reflexive relative to M if whenever ϕ,ψ ∈ R[M]with ϕR[M]ψ =0,then ψR[M]α(ϕ)=0.A ring R is called strongly M-α-refleixve if there exists a strongly refleixve endomorphism α of R relative to M.
Remark (i)A ring R is strongly M-reflexive if R is strongly M-1R-reflexive,where 1Ris the identity endomorphism of R.(ii)Every subring S with α(S) ⊆ S of a strongly M-αreflexive is also strongly M-α-reflexive.(iii)For any i∈ I,let Ribe a strongly M-αi-reflexive ring with αian endomorphism of Ri.Then S= Πi∈IRiis strongly M-α-reflexive,where the endomorphism α of S is defined by:

(iv)If M={e},then every α-reflexive ring is strongly M-α-reflexive,and let M=(N∪{0},+).Thus,a ring R is strongly M-α-reflexive if and only if R is α-reflexive.
The next example shows that α-reflexive rings need not be strongly M-α-reflexive.
Example 2.1 Let R be a α-reflexive ring with an endomorphism α.Suppose S=M2(R).Then S is an¯α-reflexive ring by[5,Theorem 3.3].However,let
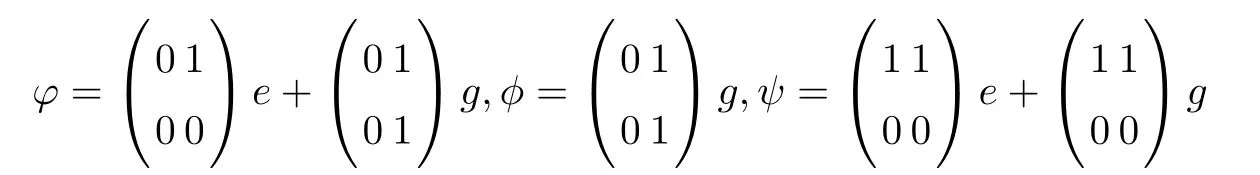

Thus S is not a strongly M-¯α-reflexive.
A monoid M is called a u.p.-monoid(unique product monoid)if for any two nonempty finite subsets A,B∈M,there exists an element g∈M uniquely in the form of ab with a∈A and b∈ B.Every u.p.-monoid M has no nonunity element of finite order.Let(M,„)be an ordered monoid.If for any g,g0,h∈M,g≺ g0implies that gh≺ g0h and hg≺ hg0,then(M,„)is called a strictly ordered monoid.
Lemma 2.3[9,Lemma1]Let M be a u.p.-monoid and R a reduced ring.Then R[M]is reduced.
Lemma 2.4[10,Corollary2.3]Let M be a strictly totally ordered monoid and R a reduced ring.Then R[M]is reduced.
Theorem 2.5 Let M be a u.p.-monoid and R a reduced ring.If R is α-reflexive,then R is strongly M-α-reflexive.
ProofLet ϕ =a1f1+···+anfnand ψ =b1h1+···+bmhm∈ R[M],be such that ϕφψ =0 for all φ =c1g1+ ···+ckgk.It is obvious that R is a 3-M-Armendariz ring,since R is reduced by[13,Proposition 1]and[8,Theorem 2.6].Thus aickbj=0,for all i,j,k.With these facts and the fact that R is α-reflexive,we have bjckα(ai)=0.Then ψφα(ϕ)=0.This means that R is strongly M-α-reflexive.
Corollary 2.6 Let R be a 3-M-Armendariz ring.Then R is α-reflexive if and only if R is strongly M-α-reflexive.
Corollary 2.7 Let M be a strictly totally ordered monoid and R a reduced ring.If R is α-reflexive,then R is strongly M-α-reflexive.
Lemma 2.8 Let M be a u.p.-monoid and R be a α-rigid ring.Then R[M]is α-rigid.
Proof Since R is α-rigid if and only if R is α-compatible and reduced,thus R[M]is reduced by Lemma 2.3.We will show that R[M]is also α-compatible.Let ϕ =aigi,ψ=bjhjbe in R[M]with ϕψ =0.Since R reduced rings are M-Armendariz rings by[7,Proposition 1.1],we obtain that aibj=0.With these facts and the fact that R is α-compatible,we have aiα(bj)=0,thus ϕα(ψ)=0.This means that R[M]is α-compatible.
An element u of a ring R is called right(resp.,left)regular if ur=0(resp.,ru=0)implies r=0 for r∈R.An element is regular if it is both left and right regular.Recall that a ring R is called right(resp.,left)Ore if given a,b∈R with b regular,there exist a1,b1∈R with b1regular such that ab1=ba1(resp.,b1a=a1b).We suppose that the classical right quotient ring Q of R exists.Then for an automorphism α of R and any ab−1∈ Q where a,b∈ R with b regular,the induced map¯α:Q→Q defined by¯α(ab−1)=α(a)α(b)−1is also an endomorphism.Accordingly,we have the following result.
Theorem 2.9 Let M be a u.p.-monoid and R a right Ore ring with classical right quotient ring Q.If α is an epimorphism of R such that R is an α-rigid ring,then R is strongly M-αreflexive if and only if Q is strongly M-¯α-reflexive.
Proof Assume that R is strongly M-α-reflexive.Let ϕ =be in

Then by[14,Proposition 2.1.16],we assume that ui=aiδ−1,vj=bjη−1,wk=ckθ−1with ai,bj,ck∈ R for all i,j,k and some regular elements δ,η,θ∈ R.Moreover,for each k,j,there exist dk,ej∈ R and regular elementsµ,ξ∈ R such that δ−1ck=dkµ−1,(θµ)−1bj=ejξ−1alsoby[14,Proposition 2.1.16].Suppose thatFrom Eq.(2.1),we have the following equation:
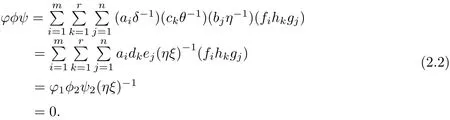
Eq.(2.2)implies that ϕ1φ2ψ2=0.
Since ϕ1φ2ψ2=0,we get α(ϕ1φ2ψ2)=0,i.e., α(ϕ1)α(φ2ψ2)=0.With the fat that R is α-rigid if and only if R is α-compatible and reduced,we have that R[M]is α-compatible and reduced by Lemma 2.8.It follows that α(ϕ1)(φ2ψ2)=0.Use the condition that R[M]is reduced and the fact that reduced rings are semicommutative.Therefore,α(ϕ1)δφ2θψ2=α(ϕ1)φ1ψ1ξ=0 and hence we have α(ϕ1)φ1ψ1=0.Using[14,Proposition 2.1.16]again,for each i,k,there exist oi,pk∈ R and regular elements σ,τ,ς∈ R such that η−1ck=pkς−1and(θς)−1α(ai)=oiτ−1.Since α is an epimorphism of R,there exists qi∈ R such that oi= α(qi)for each i.Suppose that

This shows that α(ϕ2)φ1ψ1=0.Thus ψ1φ1α(α(ϕ2))=0 since R is strongly M-α-reflexive.
Therefore,ψ1φ1α(ϕ2)=0,since R[M]is an α-compatible ring.Then

so that Q is strongly M-¯α-reflexive.
Corollary 2.10 Let R be a ring and∆a multiplicative monoid in R consisting of central regular elements.If α is an automorphism of R,then R is strongly M-α-reflexive if and only if so is∆−1R.
§3. Extensions of Strongly M-α-reflexive Rings
In this section we examine several kinds of ring extensions which play a very important role in ring theory,being concerned with strongly M-α-Reflexive rings.
Given a ring R and a(R,R)-bimodule M,the trivial extension of R by M is the ring T(R,M)=R⊕M with the usual addition and the following multiplication:(r1,m1)(r2,m2)=(r1r2,r1m2+m1r2).This is isomorphic to the ring of all matriceswhere r∈R,m ∈ M and the usual matrix operations are used.For an endomorphism α of a ring R and the trivial extension T(R,R)of R,¯α:T(R,R)→T(R,R)defined by¯α(aij)=(α(aij))is an endomorphism of T(R,R).
It is easy to see that for an α-reflexive ring R,T(R,R)need not to be an¯α-reflexive ring(see[5,Example 2.7(3),Example 3.6]).However,we have the following theorem.
Theorem 3.1 Let M be a u.p.-monoid and R a reduced ring.If R is an α-reflexive ring,then T(R,R)is a strongly M-¯α-reflexive ring.
ProofIt is obvious that T(R,R)is an¯α-reflexive ring by[4,Proposition 2.2]and a 3-MArmendariz ring by[8,Corollary 2.15].It follows that T(R,R)is a strongly M-¯α-reflexive ring by Corollary 2.6.
Let R be a ring.Define a ring S3(R)as follows:
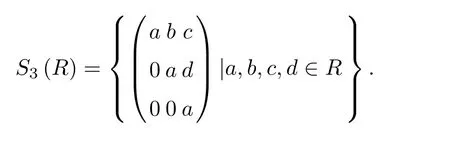
Lemma 3.2 Let M be a strictly totally ordered monoid and R a reduced ring.Then R is a 3-M-Armendariz ring.
Lemma 3.3 Let R be a reduced ring.Then aRbRb=0 if and only if aRb=0 for a,b∈R.
ProofFor a,b∈R,aRbRb=0 implies that aRbRbR=0 and(aRbR)2=aRbRaRbR⊆aRbRbR=0.Since R is reduced,then aRbR=0 and so aRb=0.The converse is obvious.
Theorem 3.4 Let M be a strictly totally ordered monoid with|M|≥2,and R a reduced ring.If R is α-reflexive ring,then S3(R)is strongly M-¯α-reflexive.
ProofIt is obvious that S3(R)is¯α-reflexive ring by[5,Theorem 3.3].Moreover,R is 3-M-Armendariz by Lemma 3.2,thus S3(R)is 3-M-Armendariz by[8,Theorem 2.12].Then,S3(R)is strongly M-¯α-reflexive by Corollary 2.6.
We denote the n×n upper triangular matrix ring over R by Tn(R),respectively.Now we study two special kinds subrings of Tn(R).Firstly,define the first special kind subring Vn(R)of Tn(R)as follows:

In view of Theorem 3.4,one may suspect that Vn(R)is strongly M-¯α-reflexive if M is a strictly totally ordered monoid and R is a reduced α-reflexive ring.But the following example eliminates the possibility.
Example 3.5 Let M be a strictly totally ordered monoid and R a reduced ring.If R is α-reflexive,then
Facing the child s clear and glistening4() eyes, the hostess was stupefied, leaning on the door feebly() and holding her face with two hands, afraid to look him in the eye.

is not strongly M-¯α-reflexive.In particular,let α be an endomorphism of V4(R)defined by¯α(1)=1,for
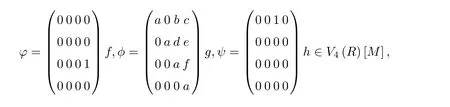
we have ϕφψ=0,but ψφ¯α(ϕ)6=0∈V4(R)[M].
Secondly,define Wn(R)as follows:

Obviously,Wn(R)is a subring of Tn(R).Then,we have the following result.
Theorem 3.6 Let M be a strictly totally ordered monoid and R a reduced ring.If R is α-reflexive,then Wn(R)is strongly M-¯α-reflexive.
Proof It is obvious that R is strongly M-α-reflexive by Corollary 2.7.Then,we use(a1,a2,···,an)∈ Wn(R)to denote
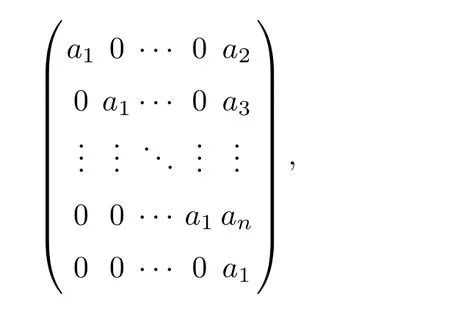
and we can denote their addition and multiplication by

So every elements in Wn(R[M])can be expressed in the form of(ϕ1,ϕ2,···,ϕn)for some ϕi’s in R[M].Let ϕ =(ϕ1,ϕ2,···,ϕn),ψ =(ψ1,ψ2,···,ψn)∈ Wn(R[M])with ϕWn(R[M])ψ =0.For any φ =(φ1,φ2,···,φn)∈ R[M],ϕφψ =0.Thus we have the following equations:


If we multiply Eq.(3.2)on the right-hand side by τψ1for any τ∈ R[M],yields ϕ1φψ2τψ1+ϕ2φψ1τψ1=0 and hence ϕ2φψ1τψ1=0,thus ϕ2R[M]ψ1=0 by Lemma 3.3 and Eq.(3.6),and ϕ1R[M]ψ2=0.Then
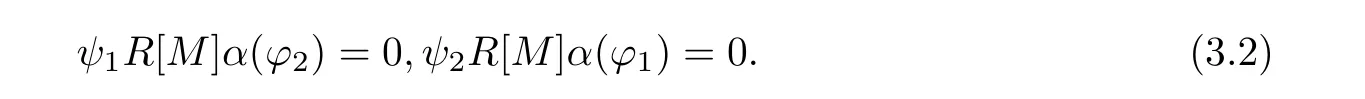
If we multiply Eq.(3.3)on the right-hand side by τψ1for any τ∈ R[M],then ϕ3R[M]ψ1=0 and ϕ1R[M]ψ3=0 by the similar argument as above.Then

Continuing this process,we multiply Eq.(3.5)on the right-hand side by τψ1for any τ∈ R[M],then ϕnR[M]ψ1=0 and ϕ1R[M]ψn=0 by the similar argument as above.Then

Thus,ψWn(R[M])¯α(ϕ)=(ψ1φ1α(ϕ1),ψ1φ1α(ϕ2)+ψ1φ2α(ϕ1)+ψ2φ1α(ϕ1),···,ψ1φ1α(ϕn)+ψ1φnα(ϕ1)+ψnφ1α(ϕ1))=0.Therefore,Wn(R)is strongly M-¯α-reflexive.
Corollary 3.7 Let M be a strictly totally ordered monoid and R a reduced ring.If R is α-reflexive,then

is strongly M-¯α-reflexive.
Ali,Elshokry and Liu[10,Proposition 2.24]have shown that if R is a reduced and strongly M-α-reversible ring,then R[M]is a strongly N-α-reversible ring,where M and N are u.p.-monoids.For strongly M-α-reflexive,we have the following results.
Proposition 3.8 Let M and N be u.p.-monoids.If R is a reduced and strongly M-αreflexive ring,then R[M]is strongly N-α-reflexive.
Proof It is obvious that R[M]is reduced by Lemma 2.3,and R[M]is α-reflexive since R is a strongly M-α-reflexive ring.Thus,R[M]is strongly N-α-reflexive by Theorem 2.5.
Proposition 3.9 Let M and N be u.p.-monoids.If R is a reduced and strongly M-αreflexive ring,then R[N]is strongly M-α-reflexive.

Proof We employ the method of[10,Proposition 2.25].It is easy to see that there exists an isomorphism of rings R[N][M]∼=R[M][N]defined by for all p,q and r,since R[M]is strongly N-α-reflexive by Proposition 3.8.So bjqckrα(aip)=0 for all i,j,k,p,q,r since R is strongly M-α-reflexive.Hence

for all p,q and r.
Also,in[10],Ali,Elshokry and Liu proved that,for arbitrary monoids M and N,if R is a reduced and strongly M-α-reversible ring,then R is strongly(M × N)-α-reversible.Similarly,we have the following proposition.
Proposition 3.10 Let M and N be u.p.-monoids.If R is a reduced and strongly M-αreflexive ring,then R is strongly(M × N)-α-reflexive.
Proof We use the similar argument to the proof of[10,Proposition 2.26].Suppose that∈ R[M × N].Without loss of generality,we assume that{n1,n2,···,ns}={n1,n2,···,nt}with ni6=njwhen 1≤ i 6=j≤ t.For any 1≤ p≤ t,denote Ap={i|1≤ i≤R[M][N].Note that mi6=mi0for any i,i0∈ Apwith i 6=i0.Now,it is obvious that there exists an isomorphism of rings R[M×N]→R[M][N]define by

Then,it is obvious that

The ring of Laurent polynomials in x,with coefficients in a ring R,consists of all formalwith obvious addition and multiplication,where mi∈R and k,n are(possibly negative)integers.Denote it by R[x;x−1].For an endomorphism α of R,we define the map:R[x;x−1]→R[x;x−1]defined byextends α and also is an endomorphism of R[x;x−1].We still denote the map¯α:R[x;x−1]→R[x;x−1]by α.
The following results extend the class of strongly M-α-reflexive rings.
Corollary 3.11 Let M be a monoid,for a ring R.If α is an endomorphism of R,then R[x]is strongly M-α-reflexive if and only if R[x;x−1]is strongly M-α-reflexive.
Proof It suffices to establish the necessity since R[x]is a subring of R[x;x−1].Suppose that R[x]is strongly M-α-reflexive.Let ∆ ={1,x,x2,···},then clearly ∆ is a multiplicative closed subset of R[x].Since R[x;x−1]= ∆−1R[x],it follows that R[x;x−1]is strongly M-αreflexive by Corollary 2.10.
It was proved in[4,Proposition 3.2]that if R is an Armendariz ring,then R is α-reflexive if and only if R[x]is α-reflexive if and only if R[x;x−1]is α-reflexive.Also in[10,Proposition 2.17],it was shown that if R is an M-Armendariz ring,then R is strongly right M-α-reversible if and only if R[x;x−1]is strongly right M-α-reversible.Accordingly,we have the equivalence on strongly M-α-reflexive rings in another situation.
Proposition 3.12 Let M be a monoid,and R a 3-M-Armendariz ring.Then the following are equivalent:
(1)R is strongly M-α-reflexive.
(2)R[x;x−1]is strongly M-α-reflexive.
Proposition 3.13 Let M be a monoid,and R be a ring,e0a central idempotent of R with α(e0)=e0.Then the following statements are equivalent:(1)R is strongly M-α-reflexive.
(2)e0R and(1−e0)R is strongly M-α-reflexive.
Proof (1) ⇔ (2)This is straightforward since subrings with α(e0)=e0and finite direct products of strongly M-α-reflexive rings are strongly M-α-reflexive.
 Chinese Quarterly Journal of Mathematics2018年3期
Chinese Quarterly Journal of Mathematics2018年3期
- Chinese Quarterly Journal of Mathematics的其它文章
- The Existence of Domain Wall Solutions in Ambjørn-Nielsen-Olesen Theory
- The Distance Energy of Circulant Graphs
- Critical Exercise Price for American Floating Strike Lookback Option in a Mixed Jump-Diffusion Model
- Estimation of Derivatives for Bounded Regular Vanishing Functions
- Generalizations of Hermite-Hadamard Type Inequalities Involving S-convex Functions
- The Maschke-type Theorems of Yetter-Drinfeld Hopf Algebras
