The Maschke-type Theorems of Yetter-Drinfeld Hopf Algebras

SHI Mei-hua,JIA Ling

(Zhejiang International Studies University,Ludong University)

Abstract:In this paper,we give the Maschke-type theorem for a Yetter-Drinfeld Hopf

Key words:Maschke-type theorem;Yetter-Drinfeld Hopf algebra;Yetter-Drinfeld Hopf module algebra;integral

It is well-known that a Hopf algebra with a projection has the Radford biproduct decomposition[4].In this decomposition one of the factors is not a Hopf algebra in the usual sense,but it is a Hopf algebra in the category of Yetter-Drinfeld modules over the other factor(the projection).There are other important examples of Hopf algebras in braided category such as(G,χ)-Hopf algebras and twisted Hopf algebras([2]).With the deeper researches many interesting results are obtained.For example,Doi considered Hopf modules in Yetter-Drinfeld category([5])and Schauenburg proved that the category of Yetter-Drinfeld modules is equivalent to the category of modules over Drinfeld double([6]).

In this paper we mainly give the Maschke-type theorem for a Yetter-Drinfeld Hopf algebra.

Conventions We work over a field k.All algebras and coalgebras are over k.For a coalgebra H we denote ∆(h)=Ph1⊗ h2and for a left H-comodule M we denote ρ(m)=idVdenotes the identity map from V to itself for any k-space V.

We first recall some basic notions.Suppose that(H,m,µ,∆,ε,S)is a Hopf algebra.A left Yetter-Drinfeld modules over H is a k-space M is endowed with both a left H-module structure by.and a left H-comodule structure by ρ verifyingP(h ·m)(−1)⊗ (h ·m)(0)=Ph1m(−1)S(h3)⊗h2·m(0).The category of Yetter-Drinfeld modules over H denoted byis a prebraided category with the prebraiding given by τM,N:M⊗N → N⊗M,τM,N(m⊗n)=·n ⊗ m(0)for two Yetter-Drinfeld modules M and N.

Definition 1[5]Let H be a Hopf algebra.An object L inD is called a Yetter-Drinfeld bialgebra if it is a k-algebra and also a k-coalgebra satisfying the following conditions for all h∈H,l,j∈L:

(1)L is an H-module algebra via the action·,that is,

(2)L is an H-module coalgebra via the action·,that is,

(3)L is an H-comodule algebra via the coaction ρ,that is,

(4)L is an H-comodule coalgebra via the coaction ρ,that is,

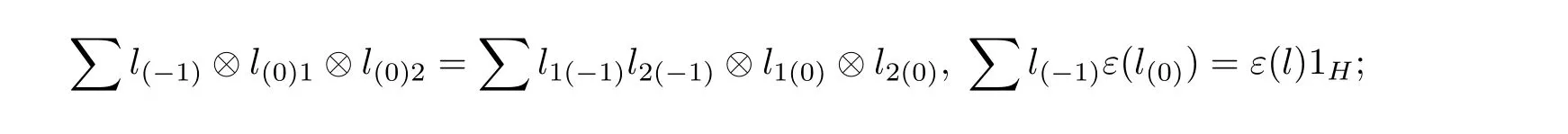
(5) ∆ and ε are algebra homomorphisms inHHY D,that is,

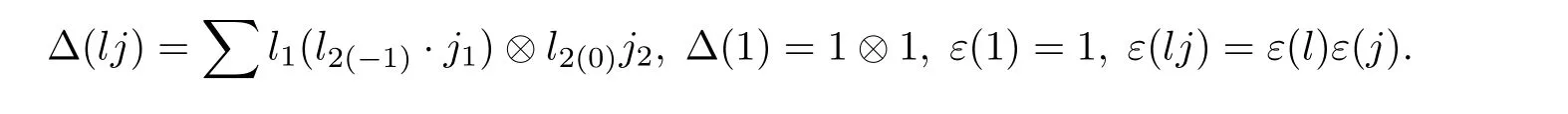
In addition,if there exists a morphism S:L→L inHHY D such that it is the convolution inverse to idL,then L is called a Yetter-Drinfeld Hopf algebra over H.

Lemma 1[5]Let L be a Yetter-Drinfeld Hopf algebra over H with the antipode S,then for any l,l0∈ L,S(ll0)=P(l(−1)·S(l0))S(l(0)),S(1)=1,∆(S(l))=Pl1(−1)·S(l2)⊗S(l1(0)),ε(S(l))= ε(l).

Definition 2 Let L be a Yetter-Drinfeld Hopf algebra over H,an element t∈L is called a right integral if tl= ε(l)t for any l∈ L.In addition,if ε(t)=1 andPt(−1)⊗ t(0)=1 ⊗ t then it is called a coinvariant normalized right integral.

Example 1 L=kZ2⊗k[Z2]is a Yetter-Drinfeld Hopf algebra over H=k[Z2]under the following structures form[7]:

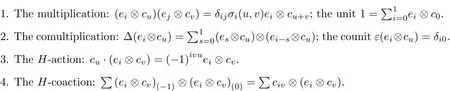
5.The antipode:S(ei⊗cu)= σi(u,−u)−1e−i⊗c−u, σ0(i,u)=1, σ1(i,u)= ιq(i,u),q(i,u)=1 if and only if i=u=1,otherwise q(i,u)=0,ι is a primitive fourth root of unity.

Definition 3 Let L be a Yetter-Drinfeld Hopf algebra over a Hopf algebra H(via the action ·and the coaction ρL)and A an algebra inHHY D(via the action*and the coaction ρA).A is called a left Yetter-Drinfeld L-module algebra if A is a left L-module(via the action◦)satisfying the following for all h∈H,y∈L,a,b∈A:

Example[8]Let L be a Yetter-Drinfeld Hopf algebra over a Hopf algebra H(via the action ·and the coaction ρ).Note that L is a left Yetter-Drinfeld L-module algebra with the action ◦given by y◦z=Py1(y2(−1)·z)S(y2(0)),y,z∈ L.Indeed,obviously 1◦x=x for any x∈L.We have to show the following equations hold.In fact,for any x,y,z∈L,

From[6]and[8-9]we know that if L is a Yetter-Drinfeld Hopf algebra over H(via the action·and the coaction ρ)and A a left Yetter-Drinfeld L-module algebra(via the L-action ◦ and H-action*),then A]L is an associative algebra which equals to A⊗L as a k-space with the multiplication given by(a]l)(b]l0)=Pa(l1◦(l2(−1)*b))]l2(0)l0for all a,b∈ A,l,l0∈ L and the unit 1A]1L.

Directly from easy computations we can obtain the following lemma.

Lemma 2 Let L be a Yetter-Drinfeld Hopf algebra over H and A be a left Yetter-Drinfeld L-module algebra,then A and L are both subalgebras of A]L.

Lemma 3 Let L be a Yetter-Drinfeld Hopf algebra over H and A be a left Yetter-Drinfeld L-module algebra,then M is a left A]L-module if and only if M is both a left A-module and a left L-module satisfyingP(l1◦(l2(−1)*a))∗(l2(0)ƒm)=lƒ(a∗m)for any a ∈ A,l∈ L,m ∈ M,where M is a left A-module via ∗ and a left L-module via ƒ.

Proof If M is a left A]L-module via ”·”,then M is a left A-module via the action given by a ∗ m=(a]1)·m and a left L-module via the action given by l ƒ m=(1]l)·m by Lemma 2.Moreover for any a ∈ A,l∈ L,m ∈ M,l ƒ(a∗m)=[(1]l)(a]1)]·m=P[l1◦(l2(−1)*a)]l2(0)]·m=P[(l1◦ (l2(−1)*a)]1)(1]l2(0))]·m=P(l1◦ (l2(−1)*a))∗ (l2(0)ƒ m).

If M is both a left A-module and a left L-module,then we claim that M is a left A]L-module via the action defined by(a]l)·m=a∗(l ƒ m).Indeed,for all a,b∈ A,l,j∈ L,m ∈ M,

Lemma 4 Let L be a Yetter-Drinfeld Hopf algebra over H with bijective antipode and A be a left Yetter-Drinfeld L-module algebra,and M,N be two A]L-modules where M and N are the left L-modules via ƒ and.and the left A-modules via ∗ and?respectively.Let t be a coinvariant normalized integral in L.If f:M→N is a left A-module map,then the mapis a left A]L-module map.

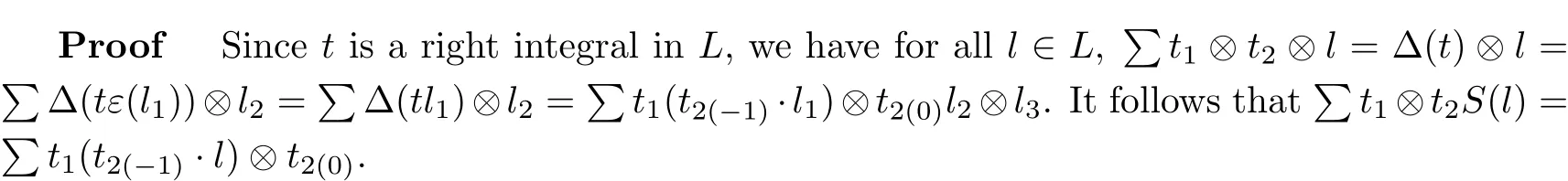
Next we will prove thatf is both a left A-module map and a left L-module map.As a matter of fact,for all l0=S(l)∈L,m∈M,

So f is also a left A-module map.By the above discussion we know thatf is a left A]L-module map.

By the above Lemma,we can obtain the Maschke-type theorem for a Yetter-Drinfeld Hopf algebra.

Theorem 1 Let L be a Yetter-Drinfeld Hopf algebra over H with bijective antipode and A be a left Yetter-Drinfeld L-module algebra,and M be an A]L-module.Let t be a coinvariant normalized integral in L and N an A]L-submodule of M.If N is an A-direct summand of M,then N is an A]L-direct summand of M.

Proof Let f:M→N be an A-module projection map.Define f:M→N,m 7→then by Lemma 4f is an A]L-module map.

In what follows we need only to show that f is a projection.Indeed,for all n∈N,f(n)=

Remark 1 If we let L:=H and define the left H-action ·on L as h ·l= ε(h)l and the left H-coaction on H as⊗l for any h ∈ H,l∈ L,then it is very easy to prove that H is a Yetter-Drinfeld Hopf algebra over H.Therefore the classical Maschke-type theorem for a Hopf algebra can be seen special case of this theorem.

AcknowledgementsWe thank all professors for their helpful comments.