一类含有中值点函数等式的证明

葛 莉，张孔生

（安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030）

含有中值点的函数等式的证明大多是通过构造辅助函数，然后论证辅助函数在给定的区间上满足相关的中值定理[1-2]，所以辅助函数的构造是证明的关键，文[3-14]对相关构造方法进行归纳和总结，提供如几何法、观察法、不定积分法、微分方程法、行列式法等。文[15]构造辅助函数法虽然多样，却不具一般性。本文对含有中值点的一类函数等式的证明作了研究，得到了辅助函数的构造公式，从而使这一类函数等式及其变形式的命题证明得以解决，并对辅助函数的构造公式做进一步推广，给出此类命题中辅助函数构造的更一般的方法。

1 形如 f′(ξ)+g(ξ)f(ξ)=0的函数等式

设f(x),g(x)在[a,b]上连续，在(a,b)内可导，且满足某些附加条件，求证：存在∃ξ∈(a,b)，使得等式f′(ξ)+g(ξ)f(ξ)=0成立。

证明的思路：要证f′(ξ)+g(ξ)f(ξ)=0 成立，

故可构造辅助函数F(x)=e∫g(x)dxf(x)，然后证明F(x)在区间[a,b]上满足罗尔定理的条件，即证得。这一类命题证明的过程如下：

（1）将要证的命题化为f′(ξ)+g(ξ)f(ξ)=0 的形式；

（2）取g(x)的一个原函数G(x)，构造辅助函数F(x)=eG(x)f(x)；

（3）F(x)=eG(x)f(x)在给定区间上满足罗尔定理的条件。

例1 已知设f(x)在[0,π]上连续，在 (0,π)内可导，求证：存在∃ξ∈(0,π)，使得f′(ξ)=f(ξ)cotξ。

分析 将要证等式化为如下形式：

取G(x)=ln sinx，

构造辅助函数F(x)=eG(x)f(x)=f(x)sinx。

证明 令F(x)=f(x)sinx，则F(0)=F(π)=0，所以F(x)在[0,π]上满足罗尔定理条件，故∃ξ∈(0,π)，使得F′(ξ)=0 ，即f′(ξ)-cotξf(ξ)=0 ，移项得证。

例 2 已知a＞0，设f(x)在[a,b]上连续，在(a,b)内可导，且f(a)=0 求证：存在 ∃ξ∈(a,b)，使得

分析 将要证等式化为如下形式：

构造辅助函数F(x)=eG(x)f(x)=(b-x)af(x)。

证明 令F(x)=(b-x)af(x)，则F(a)=F(b)=0，所以F(x)在[a,b]上满足罗尔定理条件，故∃ξ∈(a,b)，使得F′(ξ)=0 ，即

整理得证。

此形式的函数等式，还有如下其它变形式。

类型 1 形如f′(ξ)+g(ξ)(f(ξ)-a(ξ))=a′(ξ)的函数等式

分析 通过移项，则上述等式即可化为(f′(ξ)-a'(ξ))+g(ξ)(f(ξ)-a(ξ))=0 ，构造辅助函数F(x)=e∫g(x。

例3 设f(x)在[0,1]上连续，内[0,1]可导，且f(0)=0，f(1)=1，求证：∃ξ∈(0,1)，使得

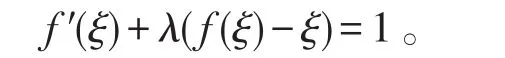
分析 移项后，则要证等式可化为如下形式：

f′(ξ)-1+λ(f(ξ)-ξ)=0 ，其中g(x)=λ，取

构造辅助函数F(x)=eG(x)(f(x)-x)=eλx(f(x)-x)。

证明 令F(x)=eλx(f(x)-x)，则F(0)=F(1)=0。

分析 将要证等式化为如下形式：从而F(x)在[0,1]上满足罗尔定理的条件，故∃ξ∈(0,1)，使得F′(ξ)=0 ，即

eλξ(f′(ξ)-1)+λeλξ(f(ξ)-ξ)=0 ，整理得证。

类型 2 形如f″(ξ)+g(ξ)f′(ξ)=0 的函数等式

分析 若u(x)=f′(x)令，则上述等式即可化为u′(x)+g(x)u(x)=0，仿第一个解法，构造辅助函数F(x)=e∫g(x)dxu(x)=e∫g(x)dxf′(x)，然后论证其在给定的闭区间上满足罗尔定理的条件即可。

例4 设f(x)在[]0,1上二阶可导，且f(0)=f(1),求证：存在 ∃ξ∈(0,1)，使得

分析 如果令f′(x)=u(x)，则要证等式可化为如下形式：，符合上述类型，其中g(x)=取G(x)=ln(1-x)2，从而构造辅助F(x)=eG(x)u(x)=(x-1)2f′(x)。

证明 令F(x)=(x-1)2f′(x)，由于f(0)=f(1)，则f(x)在[0,1]上满足罗尔定理的条件，故∃η∈(0,1)，使得f′(η)=0 ，又F(η)=F(1)=0 。所以F(x)在[η,1]上满足罗尔定理的条件，故∃ξ∈(η,1)⊂(0,1)，使得F′(ξ)=0 ，即

整理得证。

类型 3 形如g(ξ)f(t)dt+f(ξ)=0 的函数等式

例5 设f(x)在求证：∃ξ∈(0,π)，使得

证明 令F(x)=eG(x)u(x)=，则

所以F(x)在[0 , 1]上满足罗尔定理的条件，故∃ξ∈(0,1)，使得F′(ξ)=0 ，即移项得证。

对于上述构造辅助函数的方法，都可归纳为利用求解一阶线性齐次方程f′(x)+g(x)f(x)=0的通解f(x)e-∫g(x)dx=C，进而构造辅助函数F(x)=f(x)e-∫g(x)dx，那么上述函数等式可做进一步的推广。

2 形如 f′(ξ)+g(ξ)f(ξ)=h(ξ)的函数等式

证明的思路：要证f′(ξ)+g(ξ)f(ξ)=h(ξ)成立，可将等式转化为一阶线性微分方程f′(x)+g(x)f(x)=h(x)，求得通解Φ(f(x),x)=C,构造辅助函数F(x)=Φ(f(x),x)，然后证明F(x)在区间[a,b]上满足罗尔定理的条件，即证得。这一类命题证明的过程如下：

（1）将要证的命题化为微分方程f′(x)+g(x)f(x)=h(x)；

（2）求解微分方程，得通解Φ(f(x),x)=C，构造辅助函数F(x)=Φ(f(x),x)；

（3）证明F(x)在给定区间上满足罗尔定理的条件。

例 6 设ab＞0，f(x)在[a,b]上连续，在(a,b)内可导，求证：∃ξ∈(a,b)，使得

3 小结

本文通过对一类含有单中值点的函数等式进行研究，利用一阶线性微分方程的通解来构造辅助函数，得到了辅助函数的构造公式，并对辅助函数的构造公式做了进一步的推广，给出此类命题中辅助函数构造的更一般的方法，希望对于微分中值定理研究能起到一定的推进作用。