修正的Dai-Liao三项共轭梯度方法

陈贞晶

(重庆师范大学数学科学学院， 重庆 401331)

引 言

共轭梯度法是求解大规模无约束优化问题的最经典、最有效的方法之一,具有低存储要求、强收敛性、计算简单等优点。

考虑下面的无约束优化问题：

minf(x),x∈Rn

(1)

其中f:Rn→R是连续可微的。

共轭梯度法的迭代格式如下：

xk+1=xk+αkdk

(2)

d1=-g1,dk+1=-gk+1+βkdk

(3)

其中αk>0是通过某种线搜索获得的步长，dk+1是搜索方向，gk+1=g(xk+1)是目标函数f(x)在xk+1处的梯度，βk是共轭梯度法参数，简称CG参数，不同的βk值对应不同的共轭梯度方法[1]。

常用的线搜索有很多，本文只考虑Wolfe线搜索(4)-(5)和强Wolfe线搜索(4)-(6)，如下所示：

f(xk+αkdk)-f(xk)≤δαk▽f(xk)Tdk

(4)

▽f(xk+αkdk)Tdk≥σ▽f(xk)Tdk

(5)

|▽f(xk+αkdk)Tdk|≤-σ▽f(xk)Tdk

(6)

共轭条件如下所示：

(7)

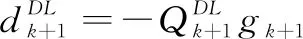
(8)

简称为DL方法且在Wolfe线搜索下满足DL共轭条件(7)，但是不满足充分下降条件

(9)

2005年，Hager和Zhang[4]提出了一种在任何线搜索下满足充分下降条件的DL类型的共轭梯度方法，简称HZ方法，如下所示：

为了得到更好的收敛性，对HZ进行非负限制，得到如下截断形式：

2011年，Narushima[5]等人提出了一类三项共轭梯度法的搜索方向的一般形式，如下所示：

(10)

2013年，Dai和Kou[6]在2013年提出一个共轭参数：

以及截断形式：

这也是一个DL类型的共轭梯度法，满足充分下降条件，是目前经典的共轭梯度方法中计算性能最佳的方法。

这个方法简称为DDL方法，在Wolfe条件下满足充分下降条件(9)，并且对一致凸函数全局收敛，在计算上与HZ、DK、DL方法作比较，结果均优于HZ、DK、DL方法，故DDL方法有效可行。

基于上述方法的优缺点，对以下两种修正的DL方法做进一步的修正，使得数值结果更加理想可行。

1 修正MDL+的方法

2017年，Narushima[8]等人对无约束优化问题，基于割线方程提出了下降的三项共轭梯度法。搜索方向和CG参数如下所示：

(11)

将其代入DL共轭条件(7)式可得出新的CG参数如下：

(12)

其中，

为了避免(12)式的分母为0，修正它为如下的形式：

(13)

其中，ξk是一个参数，定义如下:

(14)

(15)

其中，

(16)

(17)

(18)

因此，搜索方向可以表示成三项CG方法的形式，如下：

(19)

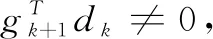
式(19)还可以写成以下三项CG形式：

(20)

其中，

(21)

基于文献[8]和[9]的思想，对文献[9]中的参数ηk运用文献[8]中的截断形式加以截断，提出以下两种截断形式，因此式(20)可以修正成以下形式：

(22)

其中，

(23)

(24)

(25)

其中，

(26)

(27)

TMDL1+算法[9]：

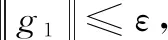
Step2计算αk使得Wolfe条件(4)-(5)成立；

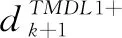
Step5令k:=k+1,转至Step2。

2 收敛性

接下来，研究TMDL1+算法的收敛性质。假设gk≠0,否则将会发现一个平稳点。为了证明TMDL1+方法全局收敛，对目标函数作以下两个基本假设[12]：

假设A：

(i)f在水平集Γ={x∈Rn：f(x)≤f(x1)}上是有界的，即存在一个数B>0,使得

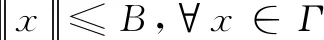
(28)

(ii)在Γ的某些邻域Ω中，f(x)是连续可微的且梯度g(x)是Lipschitz连续的，即存在L>0,使得

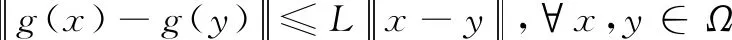
(29)

(30)

引理1(充分下降性)[6]

(31)

成立。

证明当k=0时，d1=-g1。因此不等式(31)恒成立。当k≥1时，dk+1与gk+1做内积可得：

(32)

引理2

假设目标函数满足假设A，如果步长αk满足Wolfe条件(4)-(5)，则有

(33)

接下来给出的引理3表明上述的TMDL1+算法满足Zoutendijk条件[10]。

引理3

假设序列{dk}由(22)产生，其中参数tk如(24)所示，步长αk满足Wolfe条件(4)-(5)，若f(x)满足假设A，则有Zoutendijk条件成立：

(34)

Nocedal[11]建立的以下研究结果对证明共轭梯度法的全局收敛性具有重要作用。

引理4

假设条件A对目标函数成立，考虑共轭梯度方法(2)，其中dk是下降方,步长αk满足强Wolfe条件(4)和(5)。如果

(35)

则有

(36)

对一致凸函数，我们可以证明TMDL1+算法收敛，即(36)成立。

定理5

假设目标函数f(x)满足假设条件A，如果函数f(x)是一致凸的，TMDL1+算法收敛，即(36)成立。

证明：

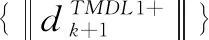
(37)

基于(24)式可知

(38)

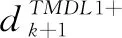
(39)

由方程(34)可得

成立。在引理4的基础上，可得：

3 数值分析

Hager和Zhang[4]在2005年提出了一个具有充分下降性的共轭梯度方法，简称HZ方法，参数如下：

以及截断形式：

Dai和Kou[6]在2013年提出一个共轭参数：

以及截断形式：

图1～图4分别对应的是HZ+、MDL+、TMDL1+、TMDL2+这四种方法解决测试问题所用的计算时间，迭代次数，函数值计算次数，梯度值计算次数的Dolan and More性能曲线图。从表1中可知数值越小，计算效果就越好，由此可以看出在计算时间上TMDL1+和TMDL2+方法优于HZ+、DK+和MDL+方法。

解决测试问题所用的计算时间，迭代次数，函数计算次数，梯度计算次数结果见表1。

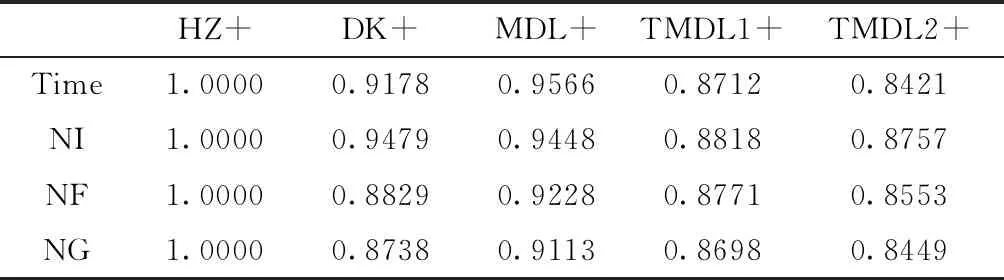
表1 测试结果

解决测试问题所用的计算时间，迭代次数，函数值计算次数，梯度计算次数的Dolan and More[13]性能曲线图如图1～图4所示：

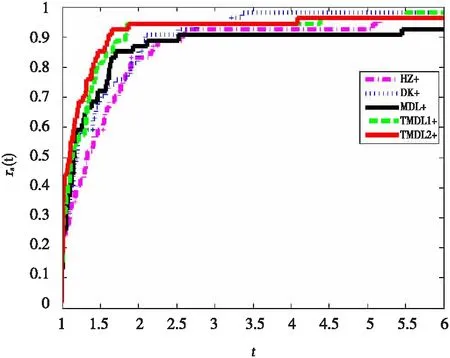
图1 计算时间

图2 迭代次数

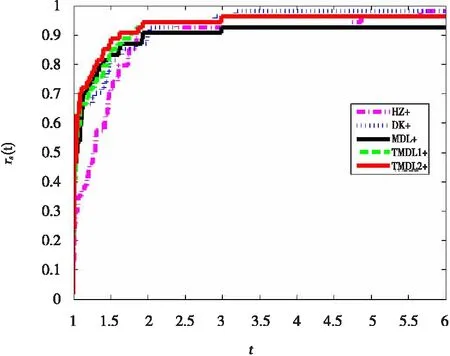
图3 函数计算次数

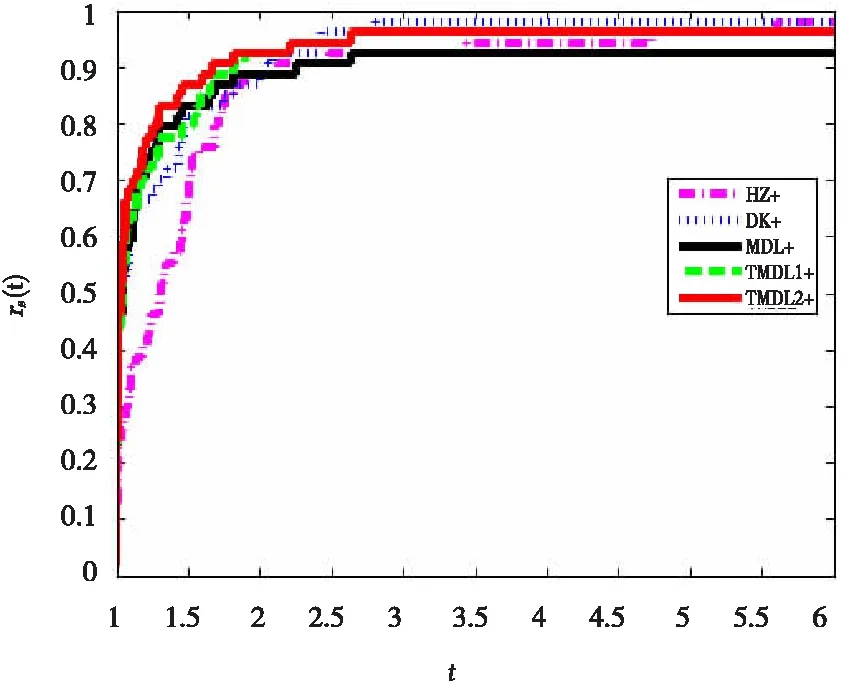
图4 梯度计算次数

因此，通过以上的表1和图1～图4可知TMDL1+和TMDL2+方法在计算时间上优于HZ+，DK+和MDL+方法，故我们的方法是有效可行的。

4 结束语

通过对三项的MDL+方法，利用HZ和DK方法的截断形式的优点和3TCG方法的截断思想，提出了MDL+方法的两种新的截断形式，简称TMDL1+和TMDL2+方法，全局收敛性与MDL+方法一致。研究表明，TMDL1+和TMDL2+方法在计算效果上优于MDL+方法和HZ+方法，是有效可行的。