黎曼面上对数函数的计算

叶薇薇，储亚伟

（阜阳师范大学 数学与统计学院，安徽 阜阳 236037）

从复流形的观点来看，黎曼面就是连通的一维凯勒流形。从局部看，一个黎曼面只是复平面中的一个开集；从整体看，黎曼面的意义在于可以在它上面能引入解析函数和亚纯函数。因此，黎曼面被认为是研究多值解析函数的整体性质的自然选择，比如像根式和对数这样的函数[1]。

在z平面上，如果需要分出多值解析函数的单值解析分支，一般可以通过割破平面的方法。以w=lnz为例，令z=reiθ，它的支点是0和∞，如果将z平面沿正实轴割开，在这样割开的区域G上，由于变点z无法围绕0或∞绕一圈，所以G上的每一点的辐角都是唯一的，从而lnz限制在G上变成单值解析函数。现在把无穷多个z平面相重叠，保证原点的位置和实轴的方向不改变，将这些平面均按照上述方法割破，记为Mk(k∈Z)。M0相当于 0＜θ＜2π ，M1相当于2π＜θ＜4π，M-1相当于-2π＜θ＜0,依次类推。接下来沿支割线将M0的上岸(θ=0)与M-1的下岸 (θ=0)粘合，M0的下岸 (θ=2π)与M1的上岸 (θ=2π)粘合，把所有的Mk(k∈Z)。用这种方法粘合在一起，就得到了w=lnz的黎曼面模型。w=lnz在每个叶片上都是单值解析的，在粘合的边界上连续并且函数值相等。在这样的黎曼面上，当点z绕z=0转回到原来位置时，它必须在每一层上转一周，此时w=lnz也在黎曼面上回到原来的位置，函数值不会改变[2]。

对于复数域上的初等多值函数，计算单值分支是其重要内容之一。许多文献以根式函数为例来讨论这部分内容[3-20]。本文将在黎曼面基础上，解决有关于对数函数的一类单值解析分支问题。

1 预备知识

定义1[12]设C是复平面内不通过点a的一条简单曲线，z0是C的起点，z1是C的终点。arg(z-a)在z0取定一值（称为arg(z-a)的初值），当z沿C从z0连续变动到z1时，arg(z-a)从连续变到（称为arg(z-a)的终值），称

为arg(z-a)在C上的直接改变量，简称辐角改变量。类似地，可定义arg(a-z)在C上的直接改变量。

定义2[21]设C是复平面内不通过点a的一条简单曲线，z0是C的起点，z1是C的终点。当z沿C从z0连续变动到z1时，向量所旋转的角称为arg(z-a)在C上的间接改变量，简称辐角改变量，记为 ΔCarg(z-a)。

引理1[21]

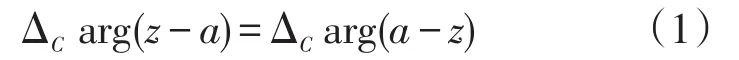
但是如果在给定的单值区域（考虑到割线因素）中来考虑多值函数的一类计算问题，使用定义1与定义2得到的辐角改变量可能不同，且公式（1）也未必成立。

本文将以对数函数为例，通过比较“间接辐角改变量法”、“直接辐角改变量法”和“限定辐角法”等方法对此进行讨论。为此，还需要给出下面的公式。

引理2[2]设D为lnf(z)的可单值分支区域，lnf(z)在z0∈D的初值为lnf(z0)的单值分支在z1∈D的终值为lnf(z1)为

其中：C为D内以为z0起点、z1为终点不穿过割线的约当曲线。

2 “间接辐角改变量法”的使用条件

命题1间接辐角改变量法的使用条件为ΔCarg(z-a)=ΔCargz′。

证明(i)设f(z)有有限支点a1,a2,…,am(m∈Z+)及∞点，将z平面按照如下方式割开，a1,a2,…,am不全落在任何一条从原点出发的射线上，而∞点在某条从原点出发的射线上l，(不妨设该射线与正实轴的夹角为α∈(-2π,0))。在这样割开后的z平面G上，f(z)可以分出单值解析分支。

由于∞点在某条从原点出发的射线上，则可限制辐角范围 argz∈(α,α+2π)(允许相差 2π 整数倍)。把单值分支在终点z1的值表示为，由命题条件 ΔCarg(z-a)=ΔCargz′，就可避免默认的变化曲线会穿过Gl之外其他割线的情形，则

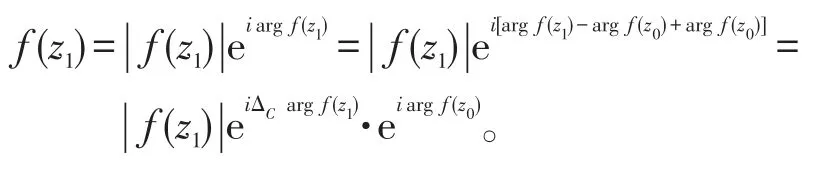
即间接算法和直接算法的结果一致。

(ii)设f(z)有有限支点a1,a2,…,am(m∈Z+)，将z平面按照如下方式割开，a1,a2,…,am不全落在任何一条从原点出发的射线上，但割线中有一段在某条从原点出发的射线上。此种情形同上可证。

以上给出使用间接辐角改变量法判断多值函数支点和确定单值分支时的条件，下面通过构造对数函数的反例来进一步验证命题的正确性。

例1在复平面内，取割线

解因f(z)的支点是0,1,∞在G内f(z)能分出三个单值解析分支。

方法一（间接辐角改变量法） 根据图1易见，当z从z0=2沿G内一条简单曲线C连续变动到zl=i时，

从而

由于f(z)在点z=2取正值，设argf(2)=0（允许相差2π的整数倍）。

由公式（2）知，

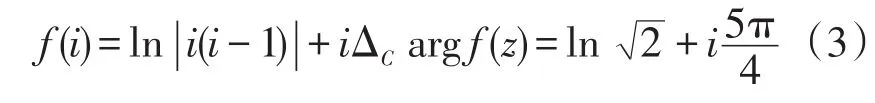
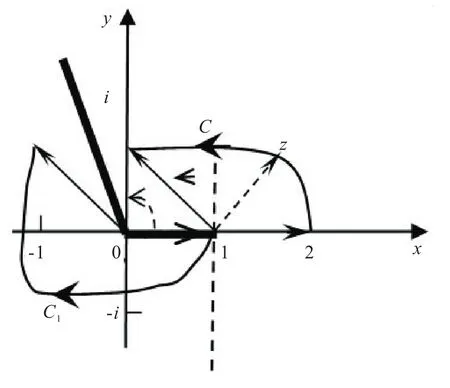
图1 例1所用图形

方法二（直接辐角改变量法） 根据图1易见，当z从z0=2沿G内简单曲线C连续变动到zl=i时，

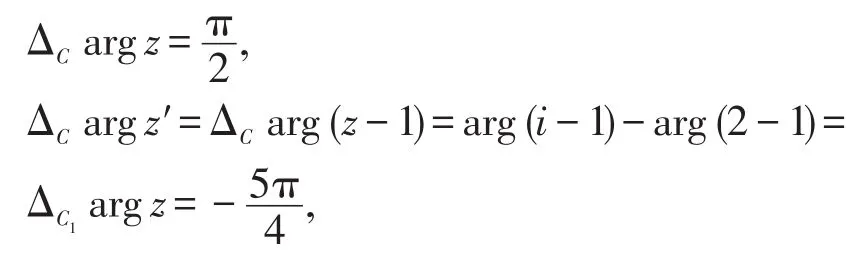
则

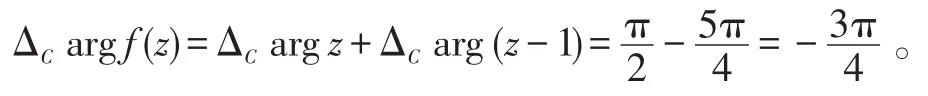
由于f(z)在点z=2取正值，设argf(2)=0（允许相差2π的整数倍）。由公式（2）知，

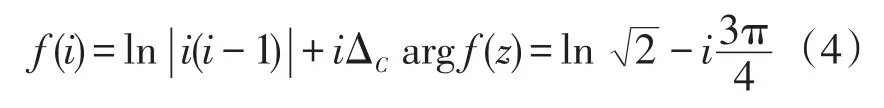
两者不同的方法得到了完全不同的答案，为了验证哪种方法是正确的，下面用限定辐角的方法方法求解。

方法三（限定辐角法） 复平面沿着0从射线y=-2x割开，由起点、终点的情况分析限定（允许相差2π的整数倍）。当z=2时，

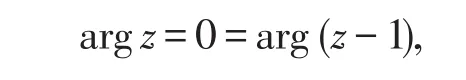
由fk(2)=ln 2+i2kπ＞0，k=0,±1,…

得k=0。当z=i时，。

从而

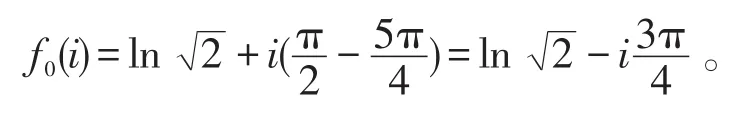
与（4）相同。

现在把问题放到黎曼面上来考虑，首先根据例1所给定的割线，建立本题f(z)=lnz(z-1)所对应的黎曼面；将三种方法进行比较，不难发现，后两种方法求得是f(z)=lnz(z-1)在第0层上z=i处的值。而由间接辐角改变量的方法一所得结果却是f(z)在第1层上z=i处的值。那么这是什么原因造成的呢？

对比间接算法与直接算法的解题过程可知，根据题目所给割线，两种算法结果不一致的原因在于

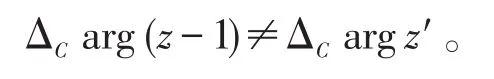
而在间接算法中计算ΔCarg(z-1)时，是先通过平移虚轴将坐标原点平移到点1，然后通过求向量所旋转的角得到ΔCarg(z-1)的。在这道题中，当平移虚轴的时候，是穿过割线的，而zl=i恰好在虚轴上。由于在黎曼面上f(z)是单值的，自变量从第0层平移到了第1层，那么求得的函数值自然也是在第1层上的了。

通过以上对实例的分析，我们发现在使用间接辐角改变量法进行计算的时候，容易出现的误区即在平移的过程中，忽略了割线的情况。

3 ΔCarg(z-a)代替ΔCarg(a-z)的条件

在对数函数的一些计算中，往往会碰到需要求ΔCarg(a-z)的情况。一般都根据引理1直接用ΔCarg(z-a)代替，然而在某些情况下二者并不相等，给解决问题带来了误区，这里给出使用ΔCarg(z-a)代替ΔCarg(a-z)的条件。

命题2计算ΔCarg(a-z)时，使用ΔCarg(z-a)代替ΔCarg(a-z)的条件是

证明类似命题1可得。为了更好地理解命题2给出的条件，下面构造一个反例。

例2设f(z)=lnz(1-z)确定在从原点起沿正实轴割破了的复平面上（如图2），求在点z0=-i的初值的那个分支z=i在值。l

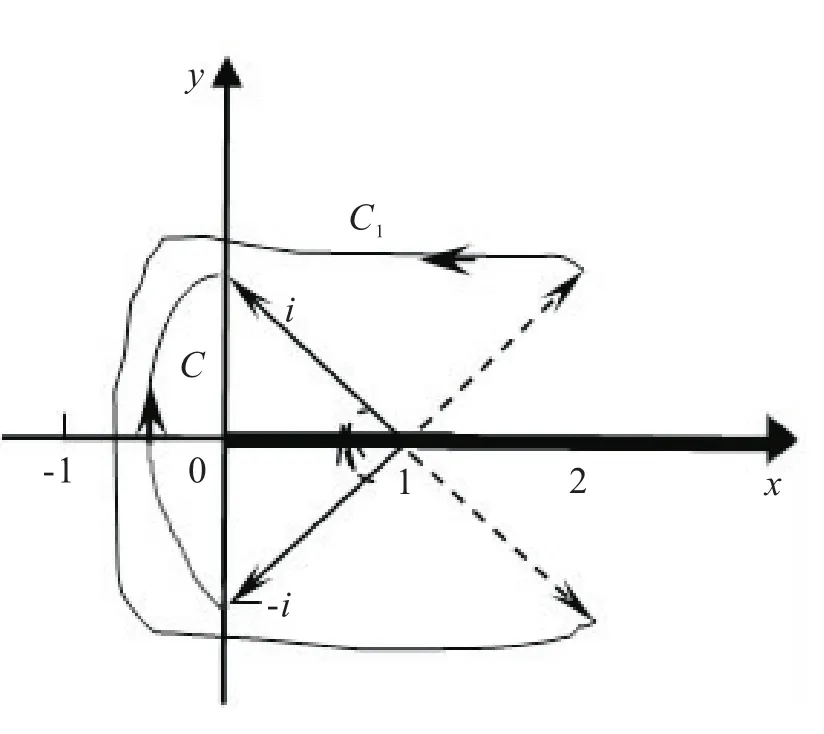
图2 例2所用图形

解法一（间接辐角改变量法）当z从z0=-i沿G内简单曲线C变动到zl=i时，如图2所示ΔCargz=-π,ΔCarg(z-1)等于向量顺时针所旋转的角，即，

于是

由公式（2）知，

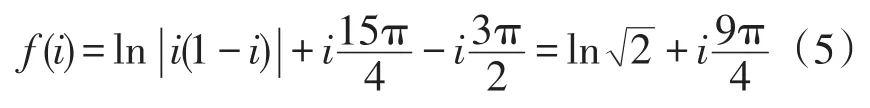
解法二（直接辐角改变量法） 当z从z0=-i沿G内简单曲线C变动到zl=i时，如图2所示

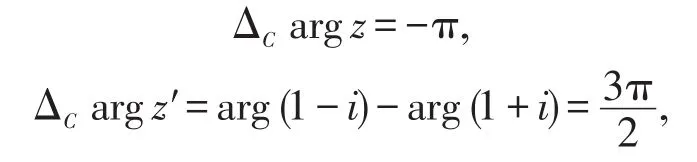
于是

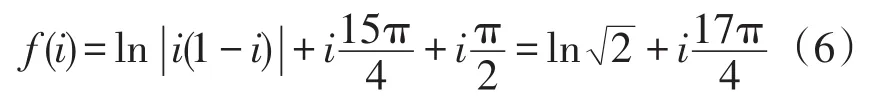
解法三（限定辐角法） 由于沿着0从正实轴割开，因此可限定argz∈(0,2π)（允许相差2π的整数倍）。于是当z0=-i时，。由

得k=1。当z=i时。故。与（6）相同。

易见造成解法一与其他两种方法计算结果不一致的原因是在计算过程中用ΔCarg(z-1)代替了ΔCarg(1-z)。然而这种代替是有问题的，在求ΔCarg(z-1)时，当z从z0=-i沿G内简单曲线C变动到zl=i时，是穿过了割线的（参图2）。在黎曼面上考虑的话，原本在第1层的自变量z按照这种路线运动的终点落到了黎曼面的第0层的z1=i处，这也是为什么解法一的计算结果与其他两种方法相差-2πi。

4 小结

本文在黎曼面上讨论对数函数的一类计算单值分支问题，可以清晰地看到在复平面上处理该类问题时，由于函数多值性所产生的两个误区。本文分别给出了有效的解决对策，为类似问题提供了参考依据。